Соотношения, описывающие изменения параметров ![]() и
и ![]() ,
характеризующие случайные доходности активов, могут быть
представлены стохастическими уравнениями. Данный подход был
реализован , в частности, в работе [7], где уравнения для
компонент вектора
,
характеризующие случайные доходности активов, могут быть
представлены стохастическими уравнениями. Данный подход был
реализован , в частности, в работе [7], где уравнения для
компонент вектора ![]() имеют вид
имеют вид
Мы будем
рассматривать следующую постановку, также предполагая, что ![]() меняются во времени, но их динамика описывается дифференциальным
включением
меняются во времени, но их динамика описывается дифференциальным
включением
Многозначная функция ![]() отражает неопределенность в изменении
доходностей. Будем предполагать, что отображение
отражает неопределенность в изменении
доходностей. Будем предполагать, что отображение ![]() кусочно
непрерывно по
кусочно
непрерывно по ![]() и при каждом фиксированном
и при каждом фиксированном ![]() множества
множества ![]() - выпуклые компакты, причем
- выпуклые компакты, причем ![]() . Матрицу
. Матрицу ![]() по-прежнему
считаем постоянной и положительно определенной.
по-прежнему
считаем постоянной и положительно определенной.
Допустим, что можно менять структуру портфеля в каждый момент
![]() с ограниченной скоростью. Динамика изменения
портфеля в этом случае описывается уравнением
с ограниченной скоростью. Динамика изменения
портфеля в этом случае описывается уравнением
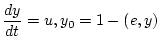 , где
, где ![]() - управляющее
воздействие, стесненное ограничением:
- управляющее
воздействие, стесненное ограничением: ![]() ;
; ![]() обладает
свойствами, аналогичными свойствам отображения
обладает
свойствами, аналогичными свойствам отображения ![]() .
.
Цель управления состоит в поддержании эффективности портфеля и
обеспечении его заданных характеристик по критериям
риск-доходность. Содержательная постановка задачи предполагает
выбор стратегии управления, реализующейся в виде управляющего
воздействия ![]() , которое формируется по доступной к моменту
времени
, которое формируется по доступной к моменту
времени ![]() информации и обеспечивает требуемые свойства портфеля.
Названная стратегия представляет собой правило, определяющее
динамику вектора распределения вложений в рисковые и безрисковый
активы.
информации и обеспечивает требуемые свойства портфеля.
Названная стратегия представляет собой правило, определяющее
динамику вектора распределения вложений в рисковые и безрисковый
активы.
Формально допустимую стратегию управления определим как
многозначное отображение
![]() , измеримое по
, измеримое по ![]() ,
полунепрерывное сверху по
,
полунепрерывное сверху по
![]() , с выпуклыми компактными
значениями
, с выпуклыми компактными
значениями
![]() .
.
Динамическая реструктуризация портфеля формализуется следующим
образом. Включения (2.1) и
Для каждого решения
![]() можно рассмотреть эволюцию характеристик портфеля,
отражающую риск и доходность:
можно рассмотреть эволюцию характеристик портфеля,
отражающую риск и доходность:
Множеству эффективных портфелей на плоскости ![]() соответствует прямая, меняющаяся во времени. Для того чтобы
портфель был эффективным, величины
соответствует прямая, меняющаяся во времени. Для того чтобы
портфель был эффективным, величины ![]() и
и ![]() должны
быть связаны соотношением
должны
быть связаны соотношением
Цель управления - поддержать эффективность портфеля в
рассматриваемом интервале времени. Рассмотрим случай, когда
безрисковая ставка постоянна ![]() , т.е.
, т.е.
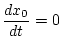 и, кроме того,
и, кроме того, ![]() .
.
Тогда
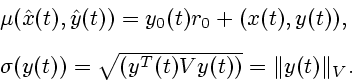
Динамическая эффективность портфеля обеспечивается равенством
![]() ,
,
![]() .
.
Пусть ![]() - эффективный портфель для
- эффективный портфель для ![]() с ожидаемым
значением доходности
с ожидаемым
значением доходности
![]() и риском
и риском
![]() .
.
Рассмотрим следующие задачи.
Задача 1. Указать допустимую стратегию управления
![]() , гарантирующую эффективность портфеля
, гарантирующую эффективность портфеля ![]() для
для
![]() , каковы бы ни были решения
, каковы бы ни были решения
![]() дифференциальных включений (2.1)-(2.2),
(2.3)-(2.4).
дифференциальных включений (2.1)-(2.2),
(2.3)-(2.4).
Задача 2. Указать допустимую стратегию управления,
которая решает задачу 1 и обеспечивает предписанный уровень риска
![]() .
.
Задача 2*. Указать допустимую стратегию управления,
которая решает задачу 1 и обеспечивает предписанный уровень
доходности
![]() .
.
Будем предполагать выполненным следующее условие
регулярности:
Д о к а з а т е л ь с т в о. Рассмотрим величину
![]() .
.
Обозначим ![]() производную функции
производную функции ![]() , которая
существует почти всюду на отрезке
, которая
существует почти всюду на отрезке
![]() .
.
Так как
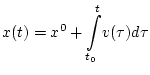 , то
, то
Учитывая, что
![]() , оценим
последнее слагаемое:
, оценим
последнее слагаемое:
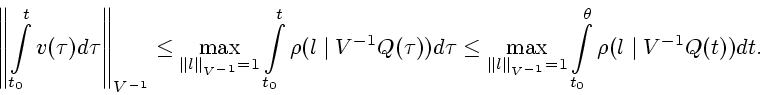
Подставляя полученную оценку в (2.7) с учетом (2.5) приходим к требуемому соотношению (2.6).
Условия разрешимости задач 1 - 2* определяются соотношением между
многозначными отображениями ![]() и
и ![]() . Ниже будет показано,
что достаточным условием разрешимости задачи 2 является
неравенство:
. Ниже будет показано,
что достаточным условием разрешимости задачи 2 является
неравенство:
Пусть
![]() - произвольное абсолютно непрерывное
решение включения (2.1)-(2.2) (по предположению
- произвольное абсолютно непрерывное
решение включения (2.1)-(2.2) (по предположению
![]() ).
).
Обозначим
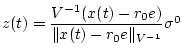 .
Полагая
.
Полагая
![]() , получим
, получим
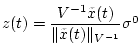 .
Обозначим через
.
Обозначим через ![]() множество значений
множество значений
![]() , отвечающих возможным реализациям
, отвечающих возможным реализациям
![]() при фиксированном значении
при фиксированном значении ![]() . В силу абсолютной
непрерывности
. В силу абсолютной
непрерывности ![]() и предположения (2.5) функция
и предположения (2.5) функция ![]() имеет почти всюду производную
имеет почти всюду производную
![]() ,
множество
,
множество ![]() составлено из значений производной тех
реализаций, для которых производная существует при данном
составлено из значений производной тех
реализаций, для которых производная существует при данном ![]() .
.
Д о к а з а т е л ь с т в о. Достаточным условием включения
![]() является
условие
является
условие
![]() для всех
для всех
![]() .
.
Пусть выполнено условие (2.8). Тогда для
![]() ,
имеем
,
имеем
![\begin{displaymath}
d\cdot\rho(l\mid P(t))\ge\sigma^0\left[ \rho(l\mid V^{-1}
Q(t))+ \max\limits_{\Vert q\Vert _V=1}\rho(q\mid Q(t))\right],
\end{displaymath}](img186.gif)
![\begin{displaymath}
\rho(l\mid P(t))\ge\frac{\sigma^0}{d}\left[
\rho(l\mid V^{-1}Q(t))+ \max\limits_{\Vert q\Vert _V=1}\rho(q\mid
Q(t))\right].
\end{displaymath}](img188.gif)
![\begin{displaymath}
\rho(l\mid
P(t))\ge\frac{\sigma^0}{\Vert\tilde{x}(t)\Vert _{...
...its_{v\in
Q(t)}\max\limits_{\Vert q\Vert _V=1} (v,q)\right]\ge
\end{displaymath}](img190.gif)
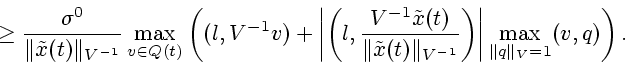
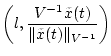 не
превосходит
не
превосходит 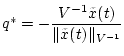 - при
- при
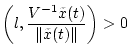 и
и
Имеем
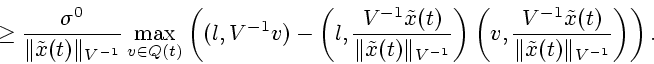
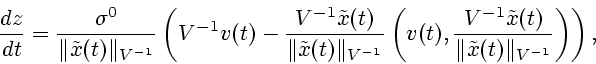
В случае, когда
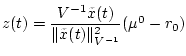 , справедливо
следующее утверждение.
, справедливо
следующее утверждение.
Доказательство аналогично доказательству леммы 4.
Из неравенства (2.5) и (2.9) выводим:
![\begin{displaymath}
\rho(l\mid
P(t))\ge \frac{(\mu^0-r_0)}{\Vert\tilde{x}(t)\Ver...
...ts_{v\in Q(t)}
\max\limits_{\Vert q\Vert _V=1}(v, q)\right]\ge
\end{displaymath}](img208.gif)
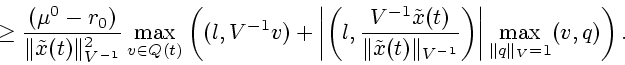
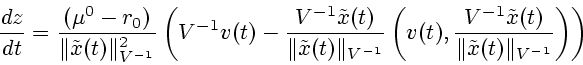
Используя леммы 4 и 5, можно установить следующий результат.
Д о к а з а т е л ь с т в о.
Построим многозначную функцию:
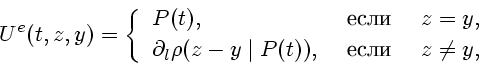
Полагая
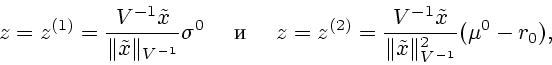
Из определения ![]() и свойств отображения
и свойств отображения ![]() следует
полунепрерывность сверху отображений
следует
полунепрерывность сверху отображений ![]() и
и ![]() по аргументам
по аргументам
![]() в области
в области
![]() и измеримость по
и измеримость по ![]() .
Таким образом, определенные выше стратегии являются допустимыми.
.
Таким образом, определенные выше стратегии являются допустимыми.
Пусть
![]() - решения включений (2.1)-(2.2),
(2.3)-(2.4), где в (2.3)
- решения включений (2.1)-(2.2),
(2.3)-(2.4), где в (2.3)
![]() .
.
Для почти всех
![]() справедлива следующая оценка:
справедлива следующая оценка:
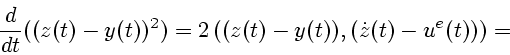
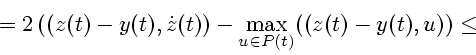
![\begin{displaymath}
{}\le
2\,[ \max\limits_{\dot{z}\in R(t)} ((z(t)-y(t), \dot{z}(t))-
\max\limits_{u\in P(t)} ((z(t)-y(t), u))]= {}
\end{displaymath}](img231.gif)
Используя лемму 4, получаем
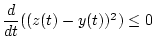 . Из последнего
неравенства и условия
. Из последнего
неравенства и условия ![]() выводим, что
выводим, что
![]() . Следовательно, портфель является эффективным и обеспечивает
заданный уровень
. Следовательно, портфель является эффективным и обеспечивает
заданный уровень
риска ![]() .
.
Если
![]() , то аналогично в
силу (2.6), (2.9) и леммы 5 снова получаем
, то аналогично в
силу (2.6), (2.9) и леммы 5 снова получаем
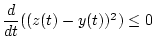 . Следовательно,
портфель является эффективным и обеспечивает заданный уровень
доходности
. Следовательно,
портфель является эффективным и обеспечивает заданный уровень
доходности ![]() .
.