1. Задача Марковица-Тобина. Стохастические модели динамического управления инвестиционным портфелем

Классическая постановка задачи выбора структуры портфеля рисковых инвестиций предполагает наличие $N$ рисковых вложений (ценных бумаг) с заданными доходностями $r_i\ \ (i=1, \ldots , N)$, которые трактуются как случайные величины. Их ожидаемые значения и матрицу ковариации обозначим через $x_i$ и $V=\{\sigma_{ij}\}$ соответственно.

Предполагается также, что имеется возможность безрисковых вложений; соответствующую доходность обозначим $x_0$. Портфель определяется вектором

$$\hat{y}=(y_0,y)^T=(y_0,y_1, \ldots y_N)^T \in R^{N+1}, \qquad \sum^N_{i=0}y_i=1,$$

каждая координата которого отвечает доле капитала, инвестируемого в соответствующий финансовый инструмент (символ "Т" означает транспонирование). Величины $y_i$ не предполагаются неотрицательными, что означает возможность получения кредита и продажи не имеющихся в наличии инструментов (short selling).

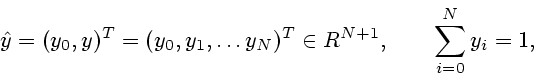
Ожидаемая доходность портфеля определяется соотношением $\mu(\hat x, \hat y) = y_0x_0+(y,x)$, где $\hat x=(x_0, x)^T$, а среднеквадратичное отклонение $\sigma(y)=(y^TVy)^{1/ 2}$ интерпретируется как соответствующий риск. Таким образом, каждому портфелю $\hat y$ на плоскости $\sigma, \mu$ (риск-доходность) соответствует определенная точка. Портфель $\hat y^*=(y^*_0, y^*)^T$ называется эффективным или недоминируемым, если не существует портфеля $\hat y$, для которого $\mu(\hat y,\hat x)\ge \mu(\hat y^*, \hat x)$ и $\sigma(y)\le\sigma(y^*)$, где по крайней мере одно из неравенств строгое.

Задача построения множества эффективных портфелей из чисто рисковых активов была поставлена и решена Г.Марковицем [2]. Это решение хорошо известно и (при условии положительной определенности матрицы $V$ и наличия у вектора $x$ различных компонент) легко может быть получено методом множителей Лагранжа. Названные условия предполагаются далее выполненными. Геометрически на плоскости $\sigma, \mu$ недоминируемым портфелям соответствует ветвь гиперболы, уравнение которой выписывается явным образом.

Наличие безрискового актива только упрощает вычисления при построении эффективного множества. Соотношение, связывающее риск и ожидаемую доходность недоминируемых портфелей, здесь линейно: $\mu=x_0+g\sigma$,

$$g^2=(x-x_0e)^TV^{-1}(x-x_0e), \quad e=(1,\ldots, 1)^T\in R^N.$$

Вектор рисковой части эффективного портфеля, соответствующего заданной доходности $\mu \ (\mu\ge r_0)$ или заданному уровню риска $\sigma$, может быть выражен следующим образом:

$$y=V^{-1}(x-x_0e)g^{-2}(\mu-r_0)$$

или

$$y=V^{-1}(x-x_0e)g^{-1}\sigma$$

соответственно.

Последние соотношения отражают, в частности, то обстоятельство, что структура рисковой части эффективных портфелей одинакова. Названный факт лежит в основе модели ценообразования САРМ: если все инвесторы руководствуются критериями риск-доходность в указанном выше смысле, то каждый из них формирует свой портфель, распределяя вложения в рисковые активы в одних и тех же пропорциях. Оптимальным в данной модели является распределение средств между двумя портфелями - безрисковым активом и рисковым портфелем фиксированной структуры. Данный результат иногда называют теоремой о двух фондах (two-fund theorem). Из этого, в свою очередь, выводится, что названная структура должна совпадать со структурой существующего реального рыночного портфеля, что дает возможность определить равновесные цены и различные характеристики реальных финансовых инструментов.

Фигурирующие в приведенных построениях доходности в простейшем случае представимы в виде 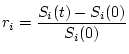$r_i={\displaystyle {\frac{S_i(t)-S_i(0)}{S_i(0)}}}$, где $S_i(t)$ - цена актива $i$ в момент времени $t$, отрезок $[0,t]$ - фиксирован. Если на допустимые значения долей капитала $y_i$ наложены дополнительные ограничения, например $y_i \ge 0$, то для нахождения множества эффективных портфелей могут быть использованы как стандартные методы математического программирования, так и специальные алгоритмы [16].

Другой подход к выбору оптимальных решений использует доверительные интервалы для случайного значения доходности портфеля $r(y)=\sum^N_{i=1}y_ir_i$. В качестве оптимального выбирается вектор $y$, решающий задачу максимизации вероятности получения заранее заданного значения доходности $a^*$:

$$P\{r(y)\ge a^*\}\to \max_y$$ (1.1)

или для фиксированного уровня $\alpha$ находится решение, максимизирующее гарантированную с вероятностью $\alpha$ доходность

$$k_\alpha(y)\to \max_y,\quad P\{r(y)\ge k_\alpha(y)\} =\alpha.$$ (1.2)

Если случайные доходности $r_i$ распределены по нормальному закону, то решение задач (1.1) и (1.2) принадлежат множеству недоминируемых портфелей.

Приведем некоторые результаты, относящиеся к задаче с непрерывным пересмотром долей портфеля в упрощенной постановке (без учета комиссии, спреда, налогов и др.). Общепринятой моделью изменения цен акций в этом случае является модель геометрического броуновского движения:

$$dS_i=S_i(x_i(t)dt +\sum\limits^N_{j=1}g_{ij}(t)d\xi_j), \quad 0\le t\le T,$$

$$S_i(0)=S^0_i.$$ (1.3)

Здесь $\xi(t)=\{\xi_1(t), \ldots , \xi_N(t)\}$ стандартный $N$-мерный винеровский процесс с независимыми компонентами, заданный на полном вероятностном пространстве $\{\Omega, \cal{F}, \Bbb{P}\}$. Через ${ \mathbb{F}} _t=\{ {\mathbb{F}}_t, 0\le t\le T \}$ обозначим естественную фильтрацию, порожденную процессом $\xi(t)$. Динамика безрисковых вложений описывается уравнением

$$dS_0=r_0(t)S_0dt, \quad 0\le t\le T,\ \ S_0(0)=S^0_0.$$ (1.4)

В простейшем случае предполагается, что параметры модели $r_0(t), \ G(t)=\{g_{ij}(t)\}\ x(t)$ - детерминированные, непрерывные функции времени $t$, матрица $G(t)$ - невырождена при всех $t$.

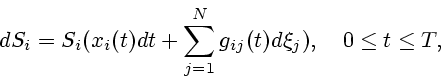
Динамика капитала, соответствующего $i$-му активу описывается в этом случае также стохастическим дифференциальным уравнением:

$$dw_i=w_i(x_i(t)dt + \sum\limits^N_{j=1}g_{ij}(t)d\xi_j)-c_i(t)dt,$$

где $c_i(t)$ - "потребление" $i$-го актива в момент $t$.

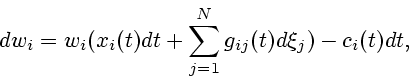
Уравнение изменения всего капитала $w(t)=w_0(t)+w_1(t)+ \ldots + w_N(t)$ имеет вид

$$dw= w[r_0(t)+y^T(x(t)-r_0(t)e)]dt + w\cdot y^T G(t)d\xi - c(t)dt,$$

$$0\le t\le T, \quad w(0)=w^0.$$ (1.5)

Здесь $c(t)=c_0(t)+c_1(t)+ \ldots +c_N(t)$ - потребление капитала в момент $t$, $y_i=y_i(t)$ - доля капитала, вложенного в $i$-й актив. Управляющие воздействия $y(t),\ c(t)$ в момент $t$ могут зависеть от всей имеющейся к этому моменту информации и формализуются в общем случае как случайные процессы, определенные на заданном вероятностном пространстве и согласованные с фильтрацией ${\mathbb{F}}_t$ . Критерием выбора оптимальных управлений является функционал

$$J(y,c)=\mbox{\sf M}\int\limits^T_0 u_1(t; c(t))dt +\mbox{\sf M}u_2(w(T)) \to \max_{y(\cdot), c(\cdot)},$$ (1.6)

где $u_1(t;w), u_2(w)$ монотонно возрастающие вогнутые по $w$ функции полезности, символ $M$ отвечает операции математического ожидания.

Класс допустимых управлений определяется таким образом, чтобы
обеспечить существование решения уравнения (1.5) и корректность определения функционала качества, а также дополнительные свойства, отражающие содержательную постановку задачи (например, неотрицательность текущего значения капитала $w(t)$ и др.)

Оптимальные по критерию (1.6) управления $y(t)$, выбираемые в подходящем классе допустимых управлений, обладают тем свойством, что при всех $t$ принадлежат множеству эффективных портфелей $Y^*(t) = \{\lambda y^*(t)\mid \lambda\ge 0\}$, где

$$y^*(t)=(G(t)G^T(t))^{-1}(x(t)-r_0(t)e).$$ (1.7)

Отсюда следует, в частности, что в динамической задаче, как и в статическом случае справедлива двухфондовая теорема [6]. Конкретный вид управлений $y(t)$ зависит от выбираемых функций полезности $u_1(t,w)$ и $u_2(w)$ [20].

В заключение данного раздела установим утверждение, относящееся к задаче квантильной оптимизации инвестиционного портфеля.

Будем рассматривать случай, когда целью управления является максимизация случайного значения капитала $w(t)$, получаемого с заданной вероятностью, а потребление на интервале $[0,T]$ отсутствует. Класс допустимых управлений $y(\cdot)$ ограничим детерминированными непрерывными функциями времени $y=y(t)$ (программные управления). Динамика изменения капитала, отвечающая фиксированному управлению $y(t)$, в этом случае описывается уравнением:

$$dw=w[r_0(t)+(x(t) -r_0(t)e)^Ty(t)]dt+ wy^T(t) G(t)d\xi,$$ (1.8)

где, как и ранее, $r_0(t), \ x(t), \ G(t)$ - детерминированные непрерывные функции времени, матрица $G(t)$ невырождена, $\xi(t)$ - стандартный $N$-мерный винеровский процесс с независимыми компонентами.

Решение стохастического дифференциального уравнения (1.8), отвечающее начальному условию $w(0)=w_0$, понимается в стандартном смысле (см., например, [21]). Рассматриваемая задача максимизации гарантированной с заданной вероятностью $\alpha$ $(\alpha \ge \frac{1}{2})$ доходности портфеля имеет вид

$$q_\alpha(T; y(\cdot))\to \max_{y(\cdot)},$$ (1.9)

$$P\{w(T; y(\cdot))\ge q_\alpha (T; y(\cdot))\}= \alpha .$$

Теорема 1   Управление

$$y_\alpha(t)= \left[ 1-\frac{k_\alpha}{\sqrt{D^*(T)}} \right]_+ y^*(t)$$

доставляет максимум среди программных управлений в задаче квантильного управления $(\ref{eq1.11})$. Здесь $k_\alpha$ - квантиль уровня $\alpha$ нормального распределения:

$$\frac{1}{\sqrt{2\pi}}\int\limits^{+\infty}_{-k_\alpha} e^{-x^2/ 2}dx=\alpha,$$

$$\quad D^*(T)={\displaystyle { \int\limits^T_0}}(x(t)- r_0(t)e)^T (G(t)G^T(t))^{-1}(x(t)-r_0(t)e)dt .$$

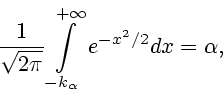
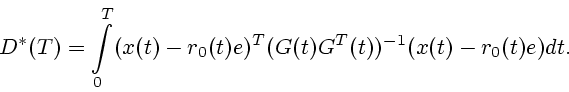
Доказательство теоремы базируется на следующих леммах.

Лемма 1   Программное управление $y(\cdot)$, оптимальное по критерию $(\ref{eq1.11})$, принадлежит множеству Парето оптимальных решений задачи:

$$\begin{array}{cc} \mbox{\sf M} (\ln (w(T, y(\cdot)))\to & \m... ...ox{\sf D}(\ln (w(T, y(\cdot)))\to & \min_{y(\cdot)}.\end{array}$$ (1.10)

Действительно, для любой непрерывной детерминированной функции $y(\cdot)$ величина $w(T, y(\cdot))$ распределена по логнормальному закону и, следовательно, для $q_\alpha(T, y(\cdot))$ имеем

$$q_\alpha(T, y(\cdot))= exp\{\mbox{\sf M}(\ln w(T, y(\cdot))) - k_\alpha \sqrt{\mbox{\sf D}(\ln w(T, y(\cdot)))}\} ,$$ (1.11)

где $k_\alpha$ - квантиль уровня $\alpha$ нормального распределения. Для математического ожидания и дисперсии величины $\ln (w(T, y(\cdot)))$ в силу (1.8) справедливы следующие представления

$$\mbox{\sf M}(\ln w(T, y(\cdot)))={}$$

$${}= \int^T_0[r_0(t) + (x(t)-r_0(t)e)^Ty(t) -\frac{1}{2} y^T(t)G(t) G^T(t)y(t)]dt+ \ln w_0,$$ (1.12)

$$\mbox{\sf D}(\ln w(T, y(\cdot)))=\int^T_0 y^T(t)G(t) G^T(t)y(t)dt.$$

Из формулы (1.11) с учетом условия $k_{\alpha}>0$ и вида (1.12) критериальных функций задачи (1.10) выводим утверждение леммы.

Лемма 2   Любое решение $y(\cdot)$ задачи $(\ref{eq1.11})$ имеет вид $y(\cdot)= \lambda y^*(\cdot)$, где $\lambda\in [0,1]$ и

$$y^*(t) = [G(t)G^T(t)]^{-1} (x(t)-r_0(t)e).$$ (1.13)

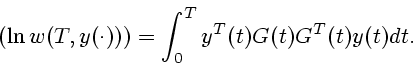
Д о к а з а т е л ь с т в о. В силу Леммы 1 каждое решение $\tilde{y}(\cdot)$ задачи (1.9) есть одновременно и решение задачи (1.10). Отсюда следует, что найдутся числа $l_1\ge 0$ и $l_2\ge 0$, не равные одновременно нулю, для которых $\tilde{y}(\cdot)$ максимизирует свертку критериев $l_1 M(\ln w(T, y(\cdot)))- l_2D(\ln w(T, y(\cdot)))$. Предполагая, что $l_2\neq 0$ и обозначая $l=l_1/l_2$, с учетом (1.12) находим явное представление для решения $\tilde{y}(\cdot): \tilde{y}(t) = \frac{l}{l+2} (G(t)G^T(t))^{-1}(x(t)-r_0(t)e)= \lambda y^*(t)$, где $\lambda=\frac{l}{l+2} \in [0,1)$. При $l_2=0$ решение имеет требуемый вид со значением $\lambda =1$.

Из доказанных лемм следует, что решение задачи (1.9) можно искать в классе управлений вида $y_{\lambda}(\cdot) = \lambda y^*(\cdot), \ \ \lambda \in [0,1]$. Подставляя $y_{\lambda}(\cdot)$ в функционал (1.10), приходим к задаче максимизации функции одного числового параметра $\lambda$, которая после несложных преобразований приводится к виду

$$\frac{1}{2}\lambda^2 - a\lambda \to \min\limits_{\lambda\in [0,1]},$$

где $a=\left( 1- k_\alpha/D^*(T)\right)$. При $a<0$ оптимальное $\lambda$ равно нулю. Последнее завершает доказательство теоремы.