6. Случай постоянной и известной величины скорости движения

В этом разделе рассмотрим случай, когда величина $V$ скорости движения ВС постоянна и заранее известна. Динамика движения будет описываться системой дифференциальных уравнений

$$\dot x = V \sin{\psi},$$

$$\dot y = V \cos{\psi},$$ (6.1)

$$\dot \psi = {ku \over V},$$

где $k= \mbox{const} >0$, $V = \mbox{const} > 0$, $\vert u\vert \le 1$.

Поскольку величина скорости зафиксирована, то ИМ есть множество в трехмерном пространстве $\{ (x, y, \psi) \}$. Соответственно, МН - трехмерное множество, цилиндрическое по координате $\psi$.

Для представления множеств ${\bf I}(t)$ будем использовать сетку по $\psi$. Каждому узлу сетки будет соответствовать сечение ${\bf I}_{\psi}(t)$ в виде выпуклого многоугольника.

Построение можно проводить по способу, изложенному в разделах 2 и 3. Однако уменьшение размерности с 4-х до 3-х позволяет использовать явные формулы при интегрировании системы (6.1) и плавающую сетку
по $\psi$.

6.1 Схема построения информационного множества

Пересчет множества ${\bf G}(t_{i})$ в множество ${\bf G}(t_{i+1})$ осуществляется следующим образом. Имеем на момент $t_{i}$ набор узлов по $\psi$. Каждому узлу соответствует выпуклый многоугольник ${\bf G}_{\psi}(t_{i})$. Используя управления $u = -1$, $0$, $1$, получим на момент $t_{i+1}$ три узла новой сетки: $\bar \psi = \psi + \Delta ku / V$. Сечения, соответствующие этим узлам, имеют вид

$${\bf G}_{\bar \psi}(t_{i+1}, u) = \left\{ \begin{array}{l} ... ... \cos{\psi} ), \mbox{~~~~~~~если~} u = 0. \end{array}\right.$$

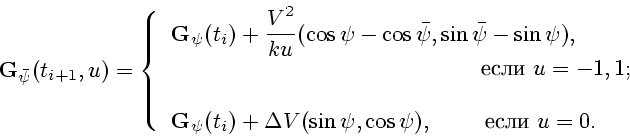
При построении множества прогноза количество узлов возрастает в три раза. Однако, поскольку все узлы расположены в интервале $[0, 2\pi]$, какие-то из них оказываются близкими, что позволяет ``объединять'' их для ограничения общего количества сечений.

Здесь вместо каждой группы сечений с близкими значениями по $\psi$, вводится одно сечение со средним значением $\psi$, представляющее собой выпуклую оболочку объединения исходных сечений, вычисляемую на векторах (3.5).

При поступлении в момент $t^*$ замера формируется множество неопределенности $H(t^*)$. Оно цилиндрично по $\psi$ и целиком определяется проекцией $H^\char93 (t^*)$ на плоскость $x, y$.

Информационное множество ${\bf I}(t^*)$ получается путем пересечения каждого сечения ${\bf G}_{\psi}(t^*)$ множества прогноза ${\bf G}(t^*)$ с множеством $H^\char93 (t^*)$. Результаты непустых пересечений и составляют искомое множество ${\bf I}(t^*)$.

6.2 Моделирование трехмерного варианта

Сначала приведем результаты, показывающие общую динамику изменения ИМ во времени. Были взяты параметры: $V = 400$ м/с, $k = 15$ м/с$^2$, $\Delta = 1$ с. Начальное информационное множество ${\bf I}(0)$ имело только одно $\psi$-сечение. Содержательно это означает, что в начальный момент времени известно направление движения. Задавалось движение истинной точки. Относительно этого движения формировались замеры. Около каждого замера строилось соответствующее множество неопределённости.

На рис. 6 показан фрагмент общей картины движения ИМ на промежутке времени 8-40 с в проекции на плоскость $x, y$. Замеры приходят в моменты 20 и 32 с. Соответствующие множества неопределенности $H^\char93$ - параллелограмм (а) и прямоугольник (b). Крестиками отмечены положения истинной точки. Заштрихованы сечения, наиболее близкие по $\psi$ к соответствующим истинным значениям. В информационных множествах отображены не все сечения, а лишь каждое второе. ИМ показаны только на каждом четвёртом шаге по времени: ${\bf I}(8)$, ${\bf I}(12)$, ${\bf I}(16)$, ..., ${\bf I}(40)$.

Рис. 6. Движение ИМ в проекции на плоскость $x$, $y$.

На рис. 7 более детально в трёхмерном пространстве изображены ИМ на моменты 20 и 32 с. Показаны множества до учета замера (множество прогноза) и после учета замера.

Рис. 7. Информационное множество до и после замера.

Результаты моделирования, где сечения ИМ задавались в виде прямоугольников со сторонами, ориентированными по осям $x$, $y$, приведены на рис. 8. Построение ИМ осуществлялось на участке времени 80 с. Использовались следующие параметры: $V = 200$ м/с, $k = 5$ м/с$^2$, $\Delta = 1$ с. Замеры поступали с интервалом 20 с, соответствующие МН имели форму квадрата со стороной 400 м. Начальное ИМ формировалось по МН начального замера и состояло из 360 одинаковых $\psi$-сечений в интервале $[0, 2\pi]$. Траектория истинного движения имела два разворота в разные стороны. МН поступающих замеров отмечены пунктиром. Показаны проекции ИМ на плоскость $x, y$ для моментов 5, 12, 27, 34, 47, 54, 67, 74 с. Проекция начального ИМ совпадает с МН замера в начальный момент. До прихода второго замера неопределённость по $\psi$ совпадает с интервалом $[0, 2\pi]$.

Рис. 8. Динамика изменения ИМ в проекции на плоскость $x$, $y$.

6.3 Сравнение с точными построениями

В работе [15] получены формулы, описывающие границу проекции на плоскость $x, y$ множества достижимости системы (6.1) в фиксированный момент времени. При этом начальное множество в начальный момент времени $t_*$ предполагается точечным, т.е. оговорено геометрическое положение $(x_*, y_*)$ и направление $\psi_*$. Обозначим проекцию на плоскость $x, y$ такого множества достижимости символом $G^\char93$. Проекцию на плоскость $x, y$ множества прогноза, строящегося по предлагаемым в работе алгоритмам, обозначим ${\bf G}^\char93$. Проведем сравнение множеств $G^\char93$ и ${\bf G}^\char93$. Такое сравнение покажет характер огрубления, которое возникает за счет применения операции овыпукления при построении сечений ИМ.

Не теряя общности, считаем начальное геометрическое положение равным нулю, а начальный угол равным $\pi/2$. На рис. 9 изображены множества $G^\char93$ и ${\bf G}^\char93$, построенные для моментов $t_{i} = i(\pi/2)(V/k)$, $i = 1, 2, 3, 4$. Данные моменты соответствуют времени поворота вектора скорости на угол $i(\pi/2)$ при движении с максимальным боковым ускорением. Для каждого момента времени использовался свой масштаб изображения. Траектории движения с экстремальными управлениями $u = -1$ и $u = 1$ представляют собой окружности радиусом $V^2/k$. Вектор начальной скорости показан стрелочкой. Множества $G^\char93$ выделены контуром и темной заливкой, а множества ${\bf G}^\char93$ - светлой заливкой. Множества ${\bf G}^\char93$ построены с мелким шагом по времени и при числе нормалей в многоугольниках $m = 64$. Использовалась достаточно мелкая сетка по $\psi$ в промежутке $[-2\pi, 2\pi]$. Видно, что ``внешние'' границы множеств $G^\char93$ и ${\bf G}^\char93$ практически совпадают, а ``внутренние'' отличаются. Имеет место вложение $G^\char93 \subset {\bf G}^\char93$.

Рис. 9. Сравнение с точным множеством достижимости.

Рис. 10. Влияние числа нормалей на точность построений.

Рис. 10 показывает зависимость точности построения от количества нормалей. Построения сделаны для момента $(5\pi/4)(V/k)$ при числе нормалей $m = 12$ и $m = 24$. При использовании $m$ больше, чем 24, картина существенно не меняется.

Подчеркнем, что граница множества $G^\char93$ описывается явными формулами лишь при точечном начальном множестве. В задачах с неполной информацией приходится строить множество прогноза от весьма произвольного начального множества. Более того, построения приходится вести в трехмерном пространстве $\{ (x, y, \psi) \}$ в случае известной величины скорости $V$ и в четырехмерном пространстве $\{ (x, y, \psi, V) \}$, когда величина скорости неизвестна. Описанный в данной работе алгоритм построения множества прогноза хотя и не дает точного множества достижимости, но оценивает его сверху и является весьма простым для реализации.

Поступила 22.10.99