П р и м е р 7.1. Пусть в (2.1), (2.2) гамильтониан ![]() определяется
равенством
определяется
равенством
![\begin{displaymath}
\left(\left\Vert l(t,x[t_{\ast }[\cdot ]t])\right\Vert^2
+h^...
...\ast
}\leq \tau \leq t}\left\Vert x[\tau ]\right\Vert \right).
\end{displaymath}](img471.gif)
В данном случае удобно взять
![\begin{displaymath}
\begin{array}{c}
P=Q=\{0\}\subset \mathbb{R},\\ [1ex]
F^{\as...
...=(l(t,x[t_{*}[\cdot ]t]),h(t,x[t_{*}[\cdot ]t]))\}.
\end{array}\end{displaymath}](img472.gif)
Тогда будут выполнены условия
(![]() ), (
), (![]() ) из п.4, при этом
включения (4.8), (4.9) обратятся в дифференциальное уравнение
с последействием
) из п.4, при этом
включения (4.8), (4.9) обратятся в дифференциальное уравнение
с последействием
Для любого начального условия
![]()
![]() согласно [1, стр.79] существует единственное решение
согласно [1, стр.79] существует единственное решение
В частности, в задаче (2.4) функционал (2.5) будет минимаксным решением.
Отметим, что если функционал (7.3) окажется ![]() -дифференцируемым,
то он будет удовлетворять уравнению (2.1), (7.1).
-дифференцируемым,
то он будет удовлетворять уравнению (2.1), (7.1).
П р и м е р 7.2. Пусть
![]() ,
,
![]() ,
,
![]()
![]() . Рассмотрим задачу
. Рассмотрим задачу
Здесь минимаксным решением является функционал
Это можно проверить взяв
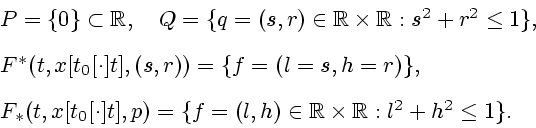
Заметим, что функционал (7.5) будет оптимальным результатом в задаче
управления системой
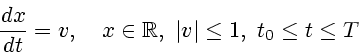
![\begin{displaymath}
\gamma =\max\{\vert x[t_1]\vert,\vert x[t_2]\vert\}+
\int\limits_{t^0}^{T}(1-v^2[t])^{1/2}dt ,
\end{displaymath}](img490.gif)
П р и м е р 7.3. Пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
Рассмотрим задачу
.
Рассмотрим задачу
Чтобы это проверить, можно взять
![\begin{displaymath}
\begin{array}{l}
P=\{p\in \mathbb{R}:\vert p\vert\leq 1\}, \...
...ast }[\cdot ]t],p)=\{f=(l=x[t-\vartheta ]+p,h=0)\}.
\end{array}\end{displaymath}](img504.gif)
Функционал (7.7) будет оптимальным результатом в задаче
управления системой с запаздыванием
![\begin{displaymath}
{dx[t] \over dt}=x[t-\vartheta ]+u,\quad x\in \mathbb{R}, \ \left\vert u\right\vert \leq 1, \
t_{0}\leq t\leq T
\end{displaymath}](img505.gif)
В примерах 7.2 и 7.3 функционалы (7.5) и (7.7) не являются
![]() -дифференцируемыми
(на
-дифференцируемыми
(на ![]() ) и удовлетворяют уравнениям
(7.4) и (7.6), соответственно, лишь в точках своей
) и удовлетворяют уравнениям
(7.4) и (7.6), соответственно, лишь в точках своей
![]() -дифференцируемости. В этих примерах
не существует непрерывных непрерывно
-дифференцируемости. В этих примерах
не существует непрерывных непрерывно ![]() -дифференцируемых решений.
-дифференцируемых решений.
Поступила 15.09.99