![\begin{displaymath}
\overline{H}(t,x[t_{*}[\cdot ]t],s,r)=\left\{
\begin{array}{...
...(t,x[t_{*}[\cdot ]t],s) & \mbox{при} \ r=0.
\end{array}\right.
\end{displaymath}](img164.gif) |
(4.1) |
Определим функционал
При условиях (a)-(d) из п.2 функционал (4.1) будет иметь следующие свойства.
![]() Для любых
Для любых
![]() функционал
функционал
![]()
![]() непрерывен на
непрерывен на ![]() .
.
(![]() ) Для любого компакта
) Для любого компакта
![]() существует
существует ![]() такое, что для всех
такое, что для всех
![]() ,
,
![]() и
и
![]() ,
,
![]() выполняется
условие Липшица по
выполняется
условие Липшица по
![]() :
:
![\begin{displaymath}
\left\vert \overline{H}(t,x^{\ast }[t_{\ast }[\cdot ]t],s,r)...
...}\left\Vert x^{\ast }[\tau ]-x^{\ast \ast }[\tau ]\right\Vert.
\end{displaymath}](img171.gif)
(![]() ) Для любых
) Для любых
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() ,
выполняется условие Липшица по
,
выполняется условие Липшица по ![]() :
:
![\begin{displaymath}
\leq L(t,x[t_{\ast
}[\cdot ]t])\left(\left\Vert s^{\prime }-...
... }\right\Vert^2+
(r^\prime -r^{\prime\prime })^2\right)^{1/2},
\end{displaymath}](img178.gif)
(![]() ) Для любой пары
) Для любой пары
![]() функция
функция
![]() положительно однородна, т.е.
положительно однородна, т.е.
Отметим также, что
Пусть ![]() и
и ![]() - некоторые непустые множества
(для определенности можно считать, что
- некоторые непустые множества
(для определенности можно считать, что ![]() и
и ![]() -
подмножества некоторых конечномерных пространств),
а многозначные отображения
-
подмножества некоторых конечномерных пространств),
а многозначные отображения
(![]() ) Для любых
) Для любых ![]() ,
, ![]() многозначные отображения
многозначные отображения
![]() и
и
![]() удовлетворяют условиям
удовлетворяют условиям ![]() -
-![]() из п.3, причем в
из п.3, причем в
![]() число
число ![]() не зависит от выбора
не зависит от выбора ![]() и
и ![]() .
.
(![]() ) Для любых
) Для любых
![]() и
и
![]() справедливы равенства
справедливы равенства
Согласно теореме Хана - Банаха
(см., например, [15, Гл. III, §2, Теорема 4])
из (![]() ), (
), (![]() ) следует
) следует
Совокупность пар
![]() (
(
![]() ),
удовлетворяющих
),
удовлетворяющих ![]() ,
, ![]() обозначим
обозначим
![]() (
(![]() ).
При условиях (a)-(d) (см. п.2)
).
При условиях (a)-(d) (см. п.2)
![]() ,
,
![]() . В частности, можно проверить, что
требования (
. В частности, можно проверить, что
требования (![]() ), (
), (![]() ) выполняются для
) выполняются для
Здесь функционал
![]() взят из условия (d).
взят из условия (d).
Отметим, что отображения из (4.6) не только полунепрерывны сверху по
включению при изменении
![]() , но и
непрерывны в метрике Хаусдорфа.
, но и
непрерывны в метрике Хаусдорфа.
Пусть
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим дифференциальные включения
Пусть
![]() ,
,
![]() ,
, ![]() .
.
Обозначим через
![]() (
(
![]() )
множество всех отвечающих паре
)
множество всех отвечающих паре ![]() решений включения (4.8)
(соответственно (4.9)) при зафиксированном
решений включения (4.8)
(соответственно (4.9)) при зафиксированном ![]() (
(![]() ).
Согласно утверждению 3.1 эти множества
будут непустыми компактами в
).
Согласно утверждению 3.1 эти множества
будут непустыми компактами в
![]() .
.
О п р е д е л е н и е 4.1. Верхним решением задачи (2.1), (2.2)
назовем полунепрерывный снизу функционал
![]() ,
удовлетворяющий неравенству
,
удовлетворяющий неравенству
О п р е д е л е н и е 4.2. Нижним решением задачи (2.1), (2.2)
назовем полунепрерывный сверху функционал
![]() ,
удовлетворяющий неравенству
,
удовлетворяющий неравенству
Заметим, что для верхних (нижних) решений ![]() в (4.11)
(
в (4.11)
(![]() в (4.13)) достигается.
в (4.13)) достигается.
О п р е д е л е н и е 4.3. Минимаксным решением задачи (2.1), (2.2)
назовем непрерывный функционал
![]() , который
одновременно будет верхним и нижним решением этой задачи.
, который
одновременно будет верхним и нижним решением этой задачи.
З а м е ч а н и е 4.1. Ниже в п. 5 будет показано, что в действительности
условия (4.11) и (4.13) выполняются для минимаксного решения
при всех
![]() и
и
![]() .
.
З а м е ч а н и е 4.2. Неравенства (4.11) и (4.13) соответствуют
условиям ![]() - и
- и ![]() -стабильности функционала цены дифференциальной
игры с наследственной информацией [2]-[8],
которые, в свою очередь, являются
отражением общего принципа оптимальности в экстремальных задачах.
-стабильности функционала цены дифференциальной
игры с наследственной информацией [2]-[8],
которые, в свою очередь, являются
отражением общего принципа оптимальности в экстремальных задачах.
Установим свойства минимаксного решения, поясняющие его связь с уравнением (2.1).
Утверждение 4.1. Если минимаксное решение ![]() -дифференцируемо в
точке
-дифференцируемо в
точке
![]()
![]() ,
то в этой точке оно удовлетворяет уравнению (2.1).
,
то в этой точке оно удовлетворяет уравнению (2.1).
Д о к а з а т е л ь с т в о.
Так как минимаксное решение ![]() при некоторой
паре
при некоторой
паре
![]() удовлетворяет условию
(4.11), то для любого
удовлетворяет условию
(4.11), то для любого ![]() существует такая функция
существует такая функция
![]() , что при всех
, что при всех
![]() справедливо неравенство
справедливо неравенство
Действительно, пусть ![]() ,
, ![]() .
Обозначим
.
Обозначим
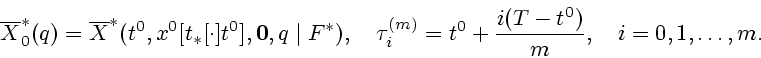
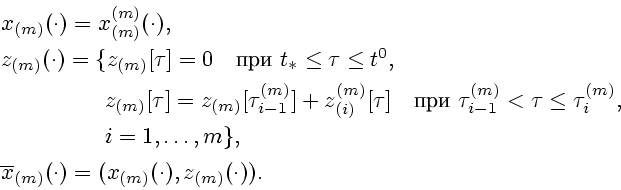
![\begin{displaymath}
\begin{array}{c}
t\in \lbrack t^{0},T],\qquad
g^{\ast }=(t,x...
...[\cdot ]\tau _{m}]),\qquad
z^{(m)}=z_{(m)}[\tau_m].
\end{array}\end{displaymath}](img243.gif)
Итак, пусть ![]() , а функция
, а функция
![]()
![]() удовлетворяет условию (4.14). Возьмем последовательность
удовлетворяет условию (4.14). Возьмем последовательность
![]() (
(![]() ),
),
![]() при
при
![]() . Так как отображение
. Так как отображение
![]() удовлетворяет требованиям (
удовлетворяет требованиям (![]() ),
то
),
то
![]() и
существуют такие
и
существуют такие
![]() (
(
![]() ), что при всех
), что при всех
![]() будут выполняться включения
будут выполняться включения
![\begin{displaymath}
\overline{x}^{\ast }[t^{0}+\delta _{i}]=
\overline{x}^{\ast ...
...}[t^{0}]+(f_{i}+f_{i}^\prime )\delta _{i},\quad
i=1,2,\ldots .
\end{displaymath}](img261.gif)
![\begin{displaymath}
{ \varphi (t^{0}+\delta _{i},x^{\ast }[t_{\ast }[\cdot ]t^{0...
...phi (t^{0},x^{0}[t_{\ast }[\cdot ]t^{0}]) \over \delta _{i}} =
\end{displaymath}](img263.gif)
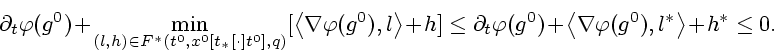
![\begin{displaymath}
=
\partial _{t}\varphi (g^{0})+\sup\limits_{q\in Q}\ \min\li...
...\left\langle
\nabla \varphi (g^{0}),l\right\rangle +h] \leq 0.
\end{displaymath}](img268.gif)
Аналогично, исходя из условия (4.13) и
учитывая (4.4), можно проверить, что также
имеет место неравенство
Утверждение доказано.
Утверждение 4.2. Если некоторый непрерывный функционал
![]() является непрерывно
является непрерывно ![]() -дифференцируемым
и удовлетворяет соотношениям (2.1), (2.2),
то он будет минимаксным решением
задачи (2.1), (2.2).
-дифференцируемым
и удовлетворяет соотношениям (2.1), (2.2),
то он будет минимаксным решением
задачи (2.1), (2.2).
Д о к а з а т е л ь с т в о.
Возьмем
![]() ,
,
![]() и
и
![]() из (4.6). Определим многозначное отображение
из (4.6). Определим многозначное отображение
![\begin{displaymath}
\begin{array}{c}
F^{0}(t,x[t_{\ast }[\cdot ]t],s,r) =\\ [2ex...
...hi (t,x[t_{\ast }[\cdot ]t]), l\right\rangle
+h]\},
\end{array}\end{displaymath}](img272.gif)
Отображения
![]() и
и
![]()
![]() непрерывны,
непрерывны,
![]() удовлетворяет условиям (
удовлетворяет условиям (![]() ).
Поэтому для отображения
).
Поэтому для отображения
![]() выполняются требования
выполняются требования ![]() -
-![]() из п.3 .
из п.3 .
Рассмотрим дифференциальное включение
Пусть
![]() (
(![]() ),
),
![]() ,
,
![]() -
множество отвечающих паре
-
множество отвечающих паре ![]() решений включения (4.19).
Понятно, что
решений включения (4.19).
Понятно, что
Пусть
![]() .
Определим функцию
.
Определим функцию
![\begin{displaymath}
\begin{array}{c} \displaystyle
{d\omega (\tau ) \over d\tau}...
...arphi (\tau ,x^{\ast }[t_{\ast
}[\cdot ]\tau ]))=0.
\end{array}\end{displaymath}](img287.gif)
Аналогично можно проверить, что он также является нижним, а стало быть, и минимаксным решением этой задачи. Утверждение доказано.