
Next: 3 Линейная задача быстродействия
Up: KISELEV
Previous: 1 Введение
Subsections
В этом разделе на примере данной простой задачи описывается схема
потенциалов; в п.п. 2.1, 2.2 рассмотрены случаи неограниченного и
ограниченного управления соответственно.
Рассмотрим задачу управления в
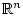 на заданном отрезке времени
на заданном отрезке времени ![$[0,T]$](img2.gif)
Здесь 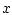 - вектор фазовых координат,
- вектор фазовых координат, 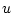 - скалярное управление.
Матрица
- скалярное управление.
Матрица
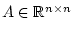 , столбец
, столбец
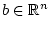 , начальное
состояние
, начальное
состояние
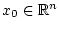 , длительность процесса
управления
, длительность процесса
управления 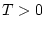 и параметр
и параметр
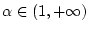 заданы.
заданы.
Задача минимизации функционала
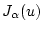 равносильна задаче минимизации нормы
равносильна задаче минимизации нормы
Предполагается выполненным условие управляемости
Поиск оптимального решения задачи (1) требует решения краевой задачи
принципа максимума Понтрягина
в которой 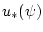 - экстремальное управление,
определяемое из условия максимума
- экстремальное управление,
определяемое из условия максимума
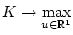 для функции
Гамильтона-Понтрягина
для функции
Гамильтона-Понтрягина
Это экстремальное управление имеет вид
При решении краевой задачи (3) подлежит определению параметр 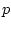 ,
являющийся
начальным значением сопряженной переменной
,
являющийся
начальным значением сопряженной переменной 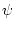 :
:
Искомое значение 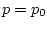 , позволяющее решить краевую задачу (3), допускает
экстремальное описание, к которому мы обратимся ниже (см. (11)).
, позволяющее решить краевую задачу (3), допускает
экстремальное описание, к которому мы обратимся ниже (см. (11)).
После нахождения вектора 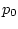 краевая задача (3) сводится к решению
задачи Коши для дифференциальных уравнений из (3) с начальными условиями
краевая задача (3) сводится к решению
задачи Коши для дифференциальных уравнений из (3) с начальными условиями
Решение
этой задачи дает решение краевой задачи (3). Оптимальное управление 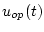 задачи (1) получаем подстановкой сопряженной переменной из (6) в формулу
(4) для экстремального управления:
задачи (1) получаем подстановкой сопряженной переменной из (6) в формулу
(4) для экстремального управления:
Оптимальная траектория 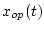 совпадает с первой
компонентой реше-
совпадает с первой
компонентой реше-
ния (6):
Оптимальное значение функционала 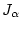 равно
равно
Неизвестное начальное значение сопряженной переменной определяется векторным
уравнением
Уравнение (7) после умножения слева на невырожденную матрицу 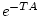 приобретает градиентную форму
приобретает градиентную форму
с потенциалом
где
Функция 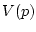 непрерывна и выпукла в
непрерывна и выпукла в
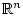 , имеет там непрерывный
градиент
, имеет там непрерывный
градиент 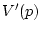 (см. (8)), причем
(см. (8)), причем
Поэтому существует минимизатор потенциала (9)
который является решением уравнения (8). Единственность решения уравнения (8)
является следствием свойства монотонности отображения 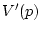 :
:
Неравенство (12) легко установить, опираясь на представление (8) градиента
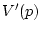 , условие (2) и строгое возрастание функции (5).
, условие (2) и строгое возрастание функции (5).
Таким образом, для
начального значения
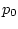 сопряженной переменной
установлена
единственность и получено экстремальное описание (11). Для вычисления
сопряженной переменной
установлена
единственность и получено экстремальное описание (11). Для вычисления
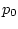 следует решить выпуклую задачу безусловной минимизации
следует решить выпуклую задачу безусловной минимизации
П р и м е р 1. При 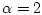 (
( 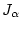 - функционал
типа "энергия") имеем
- функционал
типа "энергия") имеем
здесь
- матрица управляемости, симметричная и, при условии (2),
положительно определенная.
П р и м е р 2. При
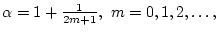 имеем
имеем
Матрица 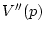 при
при 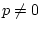 является положительно определенной.
При больших значениях
является положительно определенной.
При больших значениях 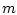 параметр
параметр 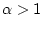 близок к единице и
функционал
близок к единице и
функционал 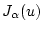 аппроксимирует функционал типа "расход топлива"
аппроксимирует функционал типа "расход топлива"
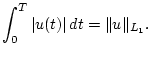
П р и м е р 3. При
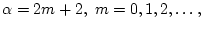 имеем
имеем
Для больших значений 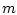 задача минимизации функционала
задача минимизации функционала
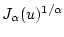 аппроксимирует задачу минимизации нормы
аппроксимирует задачу минимизации нормы
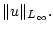
Рассмотрим теперь задачу управления (1) при ограниченном скалярном
управлении 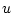 , подчиненном ограничению
, подчиненном ограничению
Кроме того, при исследовании новой задачи предполагаются выполненными
условие (2)
(которое обеспечивает локальную управляемость объекта в начале координат),
и следующее дополнительное условие на длительность процесса управления
где 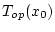 - время быстродействия для новой управляемой
системы.
- время быстродействия для новой управляемой
системы.
В последующем мы будем называть новую задачу задачей (1а).
Для задачи (1а) краевая задача принципа максимума
Понтрягина записывается в форме (3), где экстремальное управление
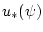 , определяемое из условия максимума
, определяемое из условия максимума
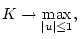 имеет вид
имеет вид
Здесь sat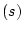 - функция насыщения, а скалярная функция
- функция насыщения, а скалярная функция
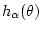 имеет
имеет
вид (5).
Искомое начальное значение сопряженной переменной, с помощью которого
разрешается
краевая задача (3), (16)-(18), определяется векторным уравнением
имеющим градиентную форму, причем
Функция 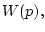 непрерывная вместе с градиентом
непрерывная вместе с градиентом 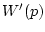 и выпуклая в
и выпуклая в
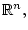 удовлетворяет условию роста
удовлетворяет условию роста
(При обосновании соотношения (22) существенно используются предположения (2)
и (15)). Поэтому существует минимизирующая точка потенциала (20)
В отличие от п. 2.1, здесь единственность минимизирующей точки имеет место
не всегда. Точка (23), решающая выпуклую задачу безусловной минимизации
является также решением уравнения (19) и это позволяет решить
краевую задачу (3), (16)-(18).
Оптимальное управление 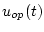 задачи (1а) определяется равенством
задачи (1а) определяется равенством
где 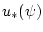 - экстремальное управление (16),
- экстремальное управление (16),
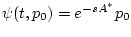 - сопряженная переменная, начальным значением
которой служит минимизирующая точка (23).
- сопряженная переменная, начальным значением
которой служит минимизирующая точка (23).
П р и м е р 4. При 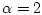 (функционал типа "энергия", см. [13])
имеем
(функционал типа "энергия", см. [13])
имеем
Обоснование свойства (22) при 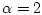 имеется в [13];
аналогичные построения позволяют установить (22) при любых
имеется в [13];
аналогичные построения позволяют установить (22) при любых
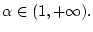
П р и м е р 5. В случае
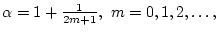 имеем
имеем
Приведенные выше результаты позволяют построить вычислительные схемы
для решения задач (1) и (1а); в этих схемах центральная роль
принадлежит решению выпуклой задачи безусловной минимизации потенциала
((13) или (24)) - простейшей задаче математического программирования.
Для решения таких задач можно рекомендовать квазиньютоновские методы [12].
После нахождения минимизатора 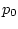 остается решить задачу Коши.
остается решить задачу Коши.


Next: 3 Линейная задача быстродействия
Up: KISELEV
Previous: 1 Введение
2003-08-11
![]() на заданном отрезке времени
на заданном отрезке времени ![]()
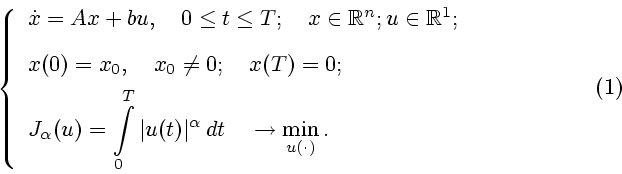
![]() - вектор фазовых координат,
- вектор фазовых координат, ![]() - скалярное управление.
Матрица
- скалярное управление.
Матрица
![]() , столбец
, столбец
![]() , начальное
состояние
, начальное
состояние
![]() , длительность процесса
управления
, длительность процесса
управления ![]() и параметр
и параметр
![]() заданы.
заданы.
![]() равносильна задаче минимизации нормы
равносильна задаче минимизации нормы
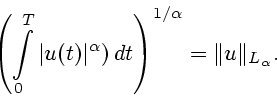
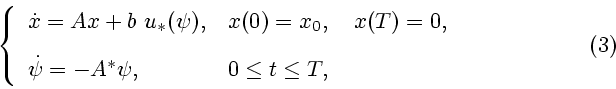
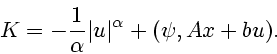
![]() краевая задача (3) сводится к решению
задачи Коши для дифференциальных уравнений из (3) с начальными условиями
краевая задача (3) сводится к решению
задачи Коши для дифференциальных уравнений из (3) с начальными условиями
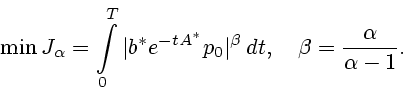
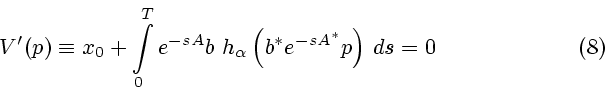
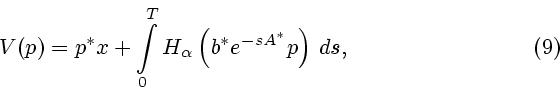
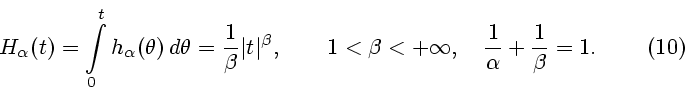
![]() непрерывна и выпукла в
непрерывна и выпукла в
![]() , имеет там непрерывный
градиент
, имеет там непрерывный
градиент ![]() (см. (8)), причем
(см. (8)), причем
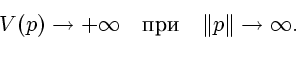

![]() сопряженной переменной
установлена
единственность и получено экстремальное описание (11). Для вычисления
сопряженной переменной
установлена
единственность и получено экстремальное описание (11). Для вычисления
![]() следует решить выпуклую задачу безусловной минимизации
следует решить выпуклую задачу безусловной минимизации

![]() (
( ![]() - функционал
типа "энергия") имеем
- функционал
типа "энергия") имеем
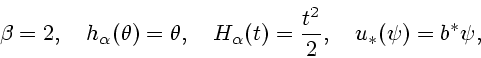
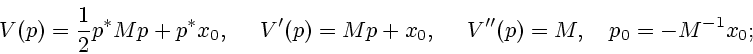
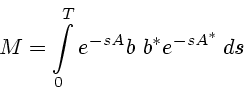
![]() имеем
имеем
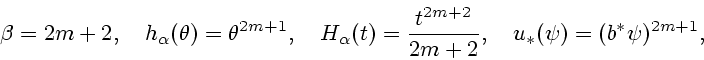
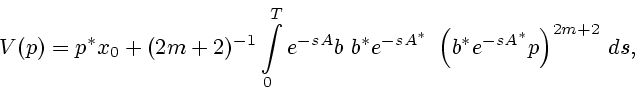
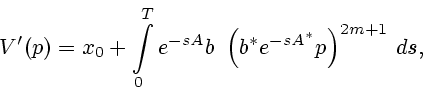
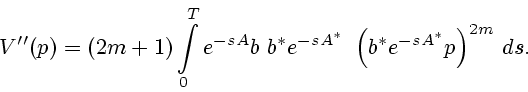
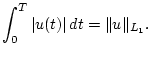
![]() имеем
имеем
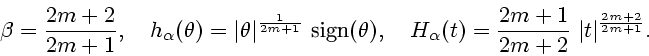
![]() задача минимизации функционала
задача минимизации функционала
![]() аппроксимирует задачу минимизации нормы
аппроксимирует задачу минимизации нормы
![]()
![]() , подчиненном ограничению
, подчиненном ограничению
![]() , определяемое из условия максимума
, определяемое из условия максимума
![]() имеет вид
имеет вид
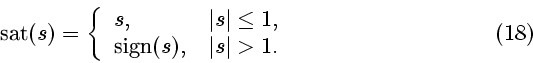
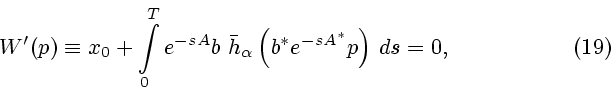
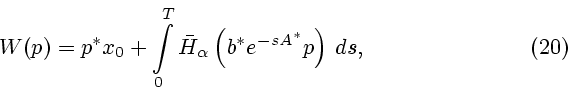



![]() (функционал типа "энергия", см. [13])
имеем
(функционал типа "энергия", см. [13])
имеем
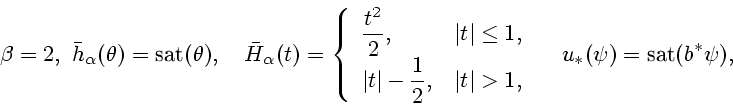
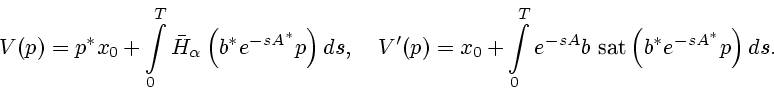
![]() имеем
имеем