3. Линейная задача быстродействия со скалярным ограниченным управлением. Метод потенциалов при специальной параметризации начального значения сопряженной переменной

Рассмотрим линейную задачу быстродействия в ${\mathbb{R}}^n$

$$\left\{ \begin{array}{l} \dot x = Ax + bu, \qquad x \in {\... ...d\ x(T) =0; \quad T \to \min. \end{array} \right. \eqno{(25)}$$

Здесь $x$ - вектор фазовых координат, $u$ - скалярное ограниченное управление. Матрица $A \in{\mathbb{R}}^{n \times n}$, столбец $b \in {\mathbb{R}}^n$ и начальное состояние $x_0 \in {\mathbb{R}}^n$ заданы. Предполагается выполненным условие локальной управляемости (2). Кроме того, предполагается, что объект переводится при некотором управлении $\vert u\vert \leq 1$ из точки $x_0$ в $0$ за конечное время.

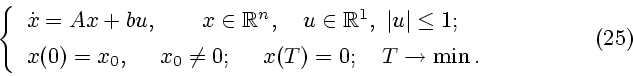
Краевая задача принципа максимума Понтрягина для задачи (25) имеет вид

$$\left\{ \begin{array}{ll} \dot x =Ax + b \ \mbox{sign}(b^*... ...- A^* \psi , & 0 \le t \le T. \end{array} \right. \eqno{(26)}$$

При решении краевой задачи (26) подлежат определению параметры

$$T=T_0 >0, \quad p=p_0=(p_1, \dots, p_n)^* \in {\mathbb{R}}^n \setminus \{ 0 \}, \eqno{(27)}$$

для которых известным образом выводится векторное уравнение

$$x_0 - \xi (p,T) = 0, \eqno{(28)}$$

где

$$\xi (p,T) = - \int\limits_0^T e^{-sA} b \ \mbox{sign} \left( b^* e^{-sA^*} p \right) \, ds \eqno{(29)}$$

- $n$-мерная ( ${\mathbb{R}}^n$-значная) нелинейная функция, удовлетворяющая условию однородности порядка нуль:

$$\xi( \lambda p, T) = \xi (p,T) \quad \forall \lambda >0\ \ \forall p \in {\mathbb{R}}^n \setminus \{ 0\}. \eqno{(30)}$$

Векторное уравнение (28) эквивалентно системе $n$ уравнений с $n+1$ неизвестными $p_1,$ $\dots,$ $p_n,T$.

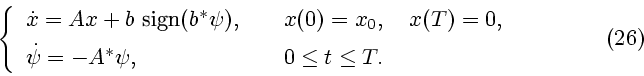
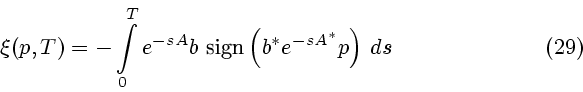
В силу (30) естественно присоединить к уравнению (28) некоторое условие нормировки, например, $\Vert p\Vert =1$; в результате этого произойдет уравнивание числа уравнений и числа неизвестных. Хорошо известно, что уравнение (28) с условием нормировки вектора $p$ может иметь много решений (возможно, компонента $p$ не единственна). Заметим, что никакой ненулевой вектор $p \in {\mathbb{R}}^n$, удовлетворяющий условию

$$p^* x_0 \ge 0, \eqno{(31)}$$

не может участвовать в решении $(p,T)$ уравнения (28), так как

$$p^* [x_0 - \xi (p,T)]= p^* x_0 + \int\limits_0^T \left\vert b^* e^{-sA^*} p \right\vert \, ds >0$$

при условиях (31), (2), $T>0,\ p \ne 0$.

Следовательно, направления $p$, подчиненные неравенству (31), можно исключить из рассмотрения. Поэтому, пользуясь свободой в выборе нормы сопряженной переменной, естественно ввести линейное "условие нормировки" неизвестного вектора $p$ в форме

$$p^* g_0 =1, \qquad g_0= - \frac{x_0}{\Vert x_0\Vert}. \eqno{(32)}$$

Условие (32) допускает любые направления вектора $p$ с отрицательным скалярным произведением $p^* x_0$. Таким образом, мы приходим к нелинейной системе уравнений

$$x_0 - \xi (p,T) =0, \eqno{(33)}$$

$$p^* g_0 =1. \eqno{(34)}$$

Скалярное уравнение (34) линейно и его общее решение имеет вид

$$p= \hat p(\eta) \equiv \ g_0 + g_1 \eta_1 + \dots + g_{n-1} \eta_{n-1} \ = \ g_0 + G \eta, \eqno{(35)}$$

где

$$g_0 = - \frac{x_0}{ \Vert x_0\Vert }, \ g_1,\dots, \ g_{n-1}$$

- ортонормированный базис в ${\mathbb{R}}^n$, $\eta=(\eta_1,\dots,\eta_{n-1})$ - вектор свободных параметров из ${\mathbb{R}}^{n-1}$, $G=(g_1\vert\dots\vert g_{n-1})$ - матрица размерности $n \times (n-1)$, образованная столбцами $g_1,\dots,g_{n-1}$.

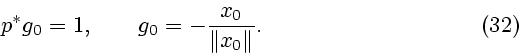
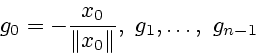
Выражение (35) определяет специальную параметризацию начального значения сопряженной переменной при помощи вектора $\eta \in {\mathbb{R}}^{n-1}$. Подстановка (35) в (33) сводит систему (33), (34) к одному векторному уравнению

$$x_0 - \xi (\hat p (\eta), T) =0, \eqno{(36)}$$

в котором число неизвестных $\eta_1,\dots,\eta_{n-1},T$ равно $n$. При умножении уравнения (36) слева на невырожденную матрицу $(\hat p (\eta)\vert g_1\vert\dots\vert g_{n-1})^*$ получим равносильную систему уравнений специального вида

$$F(\eta,T) = 0, \eqno{(37)}$$

$$F'_{\eta} (\eta, T) = 0, \eqno{(38)}$$

где скалярная функция

$$F(\eta,T) = \hat p (\eta)^* \left[ x_0 - \xi(\hat p (\eta),T... ...\vert b^* e^{-sA^*} \hat p(\eta) \right\vert \, ds \eqno{(39)}$$

называется потенциалом задачи быстродействия (25) при параметризации (35) сопряженной переменной, а ${\mathbb{R}}^{n-1}$-значная векторная функция

$$F'_{\eta} (\eta,T) = G^* [x_0 - \xi (\hat p(\eta),T)]$$

- градиент потенциала (39) по аргументу $\eta \in {\mathbb{R}}^{n-1}$. Таким образом, первое уравнение системы (37), (38) - скалярное, а ее второе уравнение (векторное уравнение в ${\mathbb{R}}^{n-1}$) имеет градиентную форму.

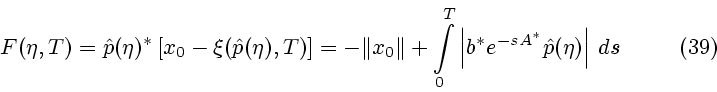
При анализе системы (37), (38) важную роль играют следующие свойства потенциала (39):

$(i)$ при любом фиксированном $\eta \in {\mathbb{R}}^{n-1}$ функция $F(\eta,T)$ строго возрастает с ростом аргумента $T>0$;

$(ii)$ функция $F(\eta,T)$ непрерывна вместе с градиентом $F'_{\eta} (\eta,T)$ при $T>0$, $\eta \in {\mathbb{R}}^{n-1}$;

$(iii)$ при любом фиксированном $T>0$ функция $F(\eta,T)$ выпукла по аргументу $\eta \in {\mathbb{R}}^{n-1}$, причем

$$F(\eta, T) \to + \infty \qquad \mbox{при } \qquad \Vert \eta \Vert \to \infty.$$

Поэтому при каждом $T>0$ существует минимизатор потенциала

$$\tilde \eta (T) = \mbox{arg} \! \! \min_{\eta \in {\mathbb{R}}^{n-1}} F(\eta, T), \eqno{(40)}$$

который служит решением уравнения (38) относительно первого аргумента. Подстановка (40) в уравнение (37) приводит к скалярному уравнению

$$\tilde F(T) =0 \eqno{(41)}$$

для определения параметра $T>0$. Здесь

$$\tilde F(T) = F( \tilde \eta (T), T) = \min_{\eta \in {\mathbb{R}}^{n-1}} F(\eta, T). \eqno{(42)}$$

Возможно, минимизирующая точка (40) не единственна. Однако функция (42) не зависит от выбора минимизатора (40). Можно показать, что функция $\tilde F(T)$ непрерывна и строго возрастает при $T>0$, а $\tilde F(+0) = -\, \Vert x_0 \Vert < 0.$ Уравнение (41) имеет единственный положительный корень $T=T_0$. Положим

$$\eta_0 =\tilde \eta (T_0), \quad p_0 = \hat p(\eta_0).$$

Тогда пара $(p_0,T_0)$ образует решение задачи (25): оптимальное время $T_{op} =T_0;$ оптимальное начальное значение сопряженной переменной $p_{op}=p_0$ или $p_{op}=\frac{p_0}{\Vert p_0\Vert};\;$ оптимальное управление $u_{op}(t)= \mbox{sign}(b^* e^{-sA^*} p_0), 0 \le t \le T_0.$

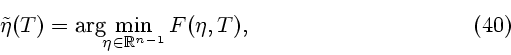
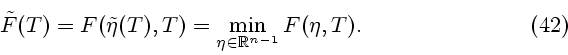
Заметим, что при сделанных предположениях оптимальное управление единственно.

Таким образом, метод потенциалов является эффективным методом как для качественного исследования, так и для построения численных алгоритмов в линейной задаче быстродействия (25). В случае гладкой линейной задачи быстродействия он излагается в [5], [6], [9]. В изложенном подходе удается естественным образом использовать присущие линейной задаче быстродействия свойства выпуклости. Применение в расчетах выпуклого потенциала (39) позволило построить эффективные схемы численного решения нелинейной краевой задачи принципа максимума Понтрягина (26), которые сохраняют работоспособность при относительно крупном шаге дискретизации по времени, позволяя заканчивать вычислительный процесс. Соответствующий итерационный процесс решения системы уравнений (37), (38) требует на каждом шаге решать задачу минимизации потенциала $F(\eta,T)$ по $\eta \in {\mathbb{R}}^{n-1}$ и задачу вычисления корня скалярного уравнения $F(\eta,T)=0$ по $T$ (гладкий случай см. в [5], [6]). Этот итерационный процесс в случае гладкой области управления обладает квадратичной скоростью сходимости [5].