4. Левосторонние решения и их замкнутые оболочки

Перейдем к исследованию ЛР задачи (2.1)-(3.1). Совокупность ЛР этой задачи обозначим символом $\mathrm{Sol}$ и положим

$$c_{*}(t, x)=\inf \,\{ c(t, x): c(\cdot) \in \mathrm{Sol}\} ,$$ (4.1)

$$c_{0}(t, x)= \displaystyle {\liminf_{(\tau, y)\rightarrow (t, x)}} \ c_{*}(\tau, y).$$ (4.2)

Пусть функция $\omega (\cdot): G^{*} \rightarrow R^1$ является минимаксным решением уравнения

$$\frac{\partial \omega (t, x)}{\partial t} + \displaystyle {\... ... -t, x)}} \ < \frac{\partial \omega (t, x)}{\partial x}, f>=0,$$

удовлетворяющим краевому условию $\omega (\theta, x)=\sigma (x)$ при всех $x\in R^n .$ Согласно [6, 21] функция $\omega (\cdot): G_{*} \rightarrow R^1$ непрерывна, $-\infty < \omega(t, x)< + \infty$ при всех $(t, x) \in G^{*}$ и, более того,

$$\omega (\theta -t, x)=\displaystyle {\max_{x(\cdot)\in X(t, x)}} \ \sigma(x(\theta)).$$ (4.3)

Утверждение 2   Для любого $c(\cdot)\in \mathrm{Sol}$ справедливо

$$c(t, x) \geq \omega (\theta -t, x) \quad \hbox{при всех} \quad (t, x)\in G^{*}$$

и, следовательно,

$$c_{*}(t, x) \geq \omega (\theta -t, x), c_{0}(t, x) \geq \omega (\theta -t, x) \quad \hbox{при всех} \quad (t, x)\in G^{*},$$

где функции $c_{*}(\cdot)$ и $c_{0}(\cdot)$ определены соотношениями $(\ref{4.1})$ и $(\ref{4.2})$.

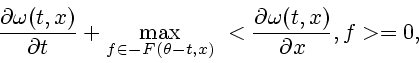
Отметим, что из этого утверждения следует, что $c_{0}(t, x)> -\infty$ при всех $(t, x) \in G^{*}.$

Приведем одно вспомогательное утверждение, с помощью которого покажем, что функция $c_{0}(\cdot): G^{*} \rightarrow R^1 ,$ определенная соотношением (4.2), является ЛР задачи (2.1)-(3.1).

Утверждение 3   Справедливо $\mathrm{epi}\ c_{0}(\cdot)= \mathrm{cl}\ \mathrm{epi}\ c_{*}(\cdot),$ где $\mathrm{cl}$ означает операцию замыкания.

Теорема 1   Функция $c_{0}(\cdot): G^{*} \rightarrow R^1 ,$ определенная соотношением $(\ref{4.2})$, является ЛР задачи $(\ref{2.1})$-$(\ref{3.1})$.

Д о к а з а т е л ь с т в о. Очевидно, что $c_{0}(0, x)\leq \sigma(x)$ при всех $x\in R^n .$ Кроме того, согласно утверждению 2, $c_{0}(t, x) \geq \omega (\theta -t, x)$ при всех $(t, x) \in G^{*}.$ Так как $\omega (\theta, x)=\sigma (x)$ при всех $x\in R^n ,$ то получаем, что $c_{0}(0, x) \geq \sigma(x)$ при всех $x\in R^n .$ Таким образом, функция $c_{0}(\cdot)$ удовлетворяет начальному условию (3.1).

Теперь докажем, что

$$\mathrm{epi}\ c_{0}(\cdot)=\tilde{H}_{-}(\theta, \mathrm{epi}\ c_{0}(\theta, \cdot)).$$ (4.4)

Так как $c_{*}(t, x)\leq c(t, x)$ при всех $(t, x) \in G^{*}$ и $c(\cdot)\in \mathrm{Sol},$ то $\mathrm{epi}\ c(\cdot) \subset \mathrm{epi}\ c_{*}(\cdot)$ для всех $c(\cdot)\in \mathrm{Sol}.$ Тогда

$$\mathrm{cl}\ \displaystyle {\bigcup_{c(\cdot) \in \mathrm{So... ...epi}\ c(\cdot)\subset \mathrm{cl}\ \mathrm{epi}\ c_{*}(\cdot).$$ (4.5)

Теперь докажем, что

$$\mathrm{cl}\ \mathrm{epi}\ c_{*}(\cdot) \subset \mathrm{cl}\... ...\bigcup_{c(\cdot) \in \mathrm{Sol}}} \ \mathrm{epi}\ c(\cdot).$$ (4.6)

Пусть $(t_{*}, x_{*}, \alpha_{*})\in \mathrm{cl}\ \mathrm{epi}\ c_{*}(\cdot).$ Тогда существуют $(t_{k}, x_{k}, \alpha_{k})\in \mathrm{epi}\ c_{*}(\cdot)$ $(k=1, 2, ...)$ такие, что $(t_{k}, x_{k}, \alpha_{k})\rightarrow (t_{*}, x_{*}, \alpha_{*})$ при $k\rightarrow \infty$ и, следовательно, $c_{*}(t_{k}, x_{k})\leq \alpha_{k}.$ Согласно определению функции $c_{*}(\cdot),$ для любого $\varepsilon_{k}>0$ $(\varepsilon_{k}\downarrow 0 \ \hbox{при} \ k \rightarrow \infty )$ существует $c_{k}(\cdot)\in \mathrm{Sol}$ такое, что $c_{k}(t_{k}, x_{k})<c_{*}(t_{k}, x_{k})+\varepsilon_{k}$ и, следовательно, $c_{k}(t_{k}, x_{k})< \alpha_{k}+\varepsilon_{k}$ при всех $k=1, 2, ...$ Это означает, что $(t_{k}, x_{k}, \alpha_{k}+\varepsilon_{k})\in \mathrm{epi}\ c_{k}(\cdot)$ при всех $k=1, 2, ...$, где $c_{k}(\cdot)\in \mathrm{Sol}.$ Отсюда вытекает, что $(t_{*}, x_{*}, \alpha_{*}) \in \mathrm{cl}\ \displaystyle {\bigcup_{c(\cdot) \in \mathrm{Sol}}} \ \mathrm{epi}\ c(\cdot).$ 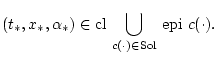Итак, справедливость включения (4.5) доказана.

Из включений (4.4), (4.5) и утверждения 3 следует, что

$$\mathrm{epi}\ c_{0}(\cdot) = \mathrm{cl}\ \displaystyle {\bigcup_{c(\cdot) \in \mathrm{Sol}}} \ \mathrm{epi}\ c(\cdot).$$ (4.7)

Согласно определению 3.1, для любого $c(\cdot)\in \mathrm{Sol}$ выполняется

$$\mathrm{epi}\ c(\cdot)=\tilde{H}_{-}(\theta, \mathrm{epi}\ c(\theta, \cdot)).$$

Тогда нетрудно установить, что

$$\mathrm{cl}\ \displaystyle {\bigcup_{c(\cdot) \in \mathrm{So... ...c(\cdot) \in \mathrm{Sol}}} \ \mathrm{epi}\ c(\theta, \cdot)),$$ (4.8)

$$\mathrm{cl}\ \displaystyle {\bigcup_{c(\cdot) \in \mathrm{So... ...pi}\ c(\theta , \cdot)= \ \mathrm{epi}\ c_{0}(\theta, \cdot)),$$ (4.9)

Учитывая соотношения (4.7) и (4.8), получаем из соотношения (4.6) справедливость равенства (4.3).

Итак, теорема доказана.

После доказательства теоремы 1 было бы полезно вернуться к утверждению 2. Заметим, что в утверждении 2 представляет интерес случай, когда $c_{0}(t, x)= \omega (\theta -t, x)$ при всех $(t, x) \in G^{*}.$

Утверждение 4   Для того, чтобы выполнялось условие $c_{0}(t, x)= \omega (\theta -t, x)$ при всех $(t, x)\in G^{*},$ необходимо и достаточно, чтобы множество $\mathrm{epi}\ \omega (\cdot)$ было положительно слабо инвариантным относительно ДВ $(\ref{2.4})$, где

$$\mathrm{epi}\ \omega (\cdot)= \{ (t, x, \alpha) \in G^{*} \times R^1 : \omega(\theta -t, x) \leq \alpha \}.$$