3 Fixed duration state constrained optimal control

The construction of a discontinuous near optimal feedback control law universal on a prescribed set first appeared in Krasovskii [31] and was elaborated upon in [32] and [33]; see also Krasovskii and Subbotin [34], [35]. Unlike these motivating seminal works, we take a proximal analytic approach in our constructions, in line with the results of the previous section on stabilizability.

Suppose that $S\subset \mathbb{R}^{n}$ is a compact set which is weakly invariant (or in alternate terminology, viable or holdable); that is, for any $(\tau ,\alpha )\in \mathbb{R}\times S$ there exists a control $% u(\cdot )$ such that $x(t)=x(t;\tau ,\alpha ,u(\cdot ))\in S$ for all $t\geq \tau$. Let $\ell :\mathbb{R}^{n}\to \mathbb{R}$ be continuous, and let $T\in \mathbb{R}$ be fixed. For an initial phase $(\tau ,\alpha )\in (-\infty ,T]\times S$, consider the following fixed time endpoint cost optimal control problem $% P(\tau ,\alpha )$ with state constraint $S$:
 
minimize $\ell (x(T))$
 
subject to
 
$\dot{x}=f(x,u),\quad x(\tau )=\alpha ,\quad x(t)\in S ~~\forall \,t\in [\tau ,T]$.
 

Let us now add the condition

(F3)

The velocity set $f(x,U)$ is convex for all $x\in \mathbb{R}^{n}$.

Then, by standard ``sequential compactness of trajectories'' arguments, the following facts are readily verified:

• The minimum in $P(\tau ,\alpha )$ is attained; we denote this minimum by $V(\tau ,\alpha )$ and refer to $V:(-\infty ,T]\rightarrow \mathbb{R}$ as the value function.

• The value function is lower semicontinuous on $(-\infty ,T]\times S$.

Remark 3.1   Note that $V$ will be continuous in the absence of a state constraint (i.e. when $S=\mathbb{R}^{n}$), but simple cases show that only lower semicontinuity holds in general. Consider, for example, the problem with $% f(x_{1},x_{2},u)=(0,u),~U=[0,1]$, where $S$ is the union of the $x_{1}$ and $% x_{2}$ axes intersecting the unit ball and where the cost is $\ell (x(1))=x_{2}(1)$. Then, $S$ is obviously weakly invariant, and if $% (x_{1}(0),x_{2}(0))=(0,0)$, the minimum value in the problem is $-1$, but for any other starting point on the $x_{1}$ axis, the minimum is $0$.

As before, by a feedback we simply mean any selection of $U$ of the form $k:\mathbb{R}\times\mathbb{R}^{n}\rightarrow U$. We will commence to sketch the method in Clarke, Rifford, and Stern [18] for producing a feedback $k$ which generates a near optimal trajectory which nearly satisfies the state constraint, with respect to the $\pi$-trajectory discretized solution concept; complete details can be found in that reference. This feedback will be operative universally for all initial phases in a specified bounded subset of $(-\infty ,T]\times S$, and it is robust with respect to measurement and external errors. The main idea is to adapt the arguments employed in [12] in proving the stabilizability result given by Theorem 2.4 above to the present problem, with the value function taking over the role played by the CLF $V$ in our prior feedback stabilizability considerations. Note well, however, that a serious technical difficulty must be overcome in achieving this: The method in Theorem 2.4 required local Lipschitzness of the CLF $V$ (in obtaining (2.11)), but the value function in the present problem may not even be continuous, as was pointed out in Remark 3.1.

We require the following notation for ``enlarged'' dynamics. For $\varepsilon > 0$, we denote

$$f_\varepsilon(x,u,v) := f(x,u) + \varepsilon v.$$ (3.1)

As before, the control function $u(\cdot )$ is valued in $U$, and now, $v(\cdot)$ is a control function valued in the closed unit ball $\bar B_n$ in $\mathbb{R}^n$. Note that feedbacks $k(t,x)$ for these dynamics will be valued in $U \times \{\varepsilon\bar B_n\}$.

Our result is the following.

Theorem 3.2   Let $t_{0}\in (-\infty ,T)$ be specified. Then, for any given $\varepsilon > 0$, there exists a feedback $k$ along with positive numbers $\delta _{0}$ and $% E_{q}$ such that, for every $\delta \in (0,\delta _{0})$, there exists $% E_{p}(\delta )>0$ as follows: for every initial phase

$$(\tau ,\alpha )\in \lbrack t_{0},T]\times S$$ (3.2)

and any partition $\pi$ of $[\tau ,T]$ with

$$\frac{\delta }{2}\leq t_{i+1}-t_{i}\leq \delta ,\quad i=0,1,\ldots ,N_{\pi }-1,~~t_{N_{\pi }}=T,$$ (3.3)

the error bounds

$$\Vert p(t_{i})\Vert \leq E_{p}(\delta ),\quad i=0,1,\ldots ,N_{\pi }-1,$$ (3.4)

$$\Vert q\Vert _{\infty }\leq E_{q}$$ (3.5)

imply that the associated $\pi$-trajectory $x_{\pi }$, with respect to $(\ref{adym})$, satisfying
$x_{\pi }(\tau )=\alpha$ also satisfies

$$\ell (x_{\pi }(T))\leq V(\tau ,\alpha )+\varepsilon$$ (3.6)

and

$$x_{\pi }(t)\in S+\varepsilon B_{n}\quad \forall \,t\in [\tau ,T].$$ (3.7)

Hence, it is asserted that the feedback $k$ produces a $\pi$-trajectory for the enlarged dynamics (3.1), which is $\varepsilon$-optimal and which remains $\varepsilon$-near $S$ in a manner which is robust and effective universally for any initial phase in the generalized rectangle $[t_0,T]\times S$.

Without loss of generality, we shall for notational ease assume $T>0$ and take $t_0=0$ in the statement of Theorem 3.2.

Define a lower semicontinuous extended real valued function $\widetilde V:\mathbb{R}\times \mathbb{R}^n \to (-\infty,\infty]$ as

$$% latex2html id marker 555\widetilde V(t,x) := \left \{ \b... ...[0,T]\times S, \\ \infty & {\rm otherwise} \end{array}\right .$$ (3.8)

Here, the value function $V$ is with respect to the original (not enlarged) dynamics. In view of the Principle of Optimality, it is readily seen that the following ``weak decrease'' property holds: For any $(\tau,\alpha)\in (-\infty,T]\times\mathbb{R}^n$, there exists a control function $u$ so that the associated trajectory of

(1.1) with $x(\tau) = \alpha$, satisfies

$$\widetilde V(t,x(t)) \leq \widetilde V(\tau,\alpha)\quad \forall \, t\in [\tau,T].$$ (3.9)

This in turn is equivalent to the following proximal Hamilton-Jacobi inequality, which is properly viewed as a type of infinitesimal decrease condition:

$$% latex2html id marker 566\bar h(x,\theta ,\zeta )\leq 0\q... ...),\quad \forall \,(t,x)\in (-\infty,T) \times \mathbb{R}^{n}.$$ (3.10)

Here the augmented lower Hamiltonian is the function $\bar h:\mathbb{R}^{n}\times \mathbb{R}\times \mathbb{R}^{n}\to \mathbb{R}$ defined by

$$\bar h(x,\theta ,\zeta ):=\theta + h(x,\zeta),$$

where $h:\mathbb{R}^n\times \mathbb{R}^n\to \mathbb{R}$ is the lower Hamiltonian

$$h(x,\zeta):=\min_{u\in U}\,\langle f(x,u),\zeta \rangle.$$

We also denote by $\bar h_\varepsilon$ the augmented Hamilton obtained from the enlarged dynamics (3.1).

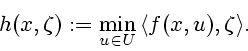
Given $\beta >0$, we now define the lower semicontinuous extended real valued function $\widetilde{V}^{\beta }:\mathbb{R}\times \mathbb{R} ^{n}\to (-\infty ,\infty ]$ as

$$% latex2html id marker 1902\widetilde{V}^{\beta }(t,x):=\w... ... [0,T]\times S, \\ \infty & {\rm otherwise} \end{array}\right.$$

A proximal calculus argument implies that $\widetilde{V}^{\beta }$ satisfies the strict infinitesimal decrease condition

$$% latex2html id marker 592\bar h(x,\theta ,\zeta )\leq -2\... ...),\quad \forall \,(t,x)\in (-\infty,T) \times \mathbb{R}^{n}.$$ (3.11)

One also has the obvious boundary conditions

$$V(T,x) = \widetilde V(T,x) = \widetilde V^\beta (T,x) = \ell (x) \quad \forall \, x\in S.$$ (3.12)

For a parameter value $\lambda >0$, we denote by $\widetilde V^\beta_\lambda$ the quadratic inf-convolution of $\widetilde V^\beta$; that is

$$% latex2html id marker 603\widetilde V^\beta_\lambda(t,x) ... ...\lambda \Vert(t^{\prime},x^{\prime})-(t,x)\Vert ^2 \right \}.$$ (3.13)

Clearly $\widetilde V^\beta$ majorizes $\widetilde V^\beta_\lambda$. Another key fact, one which enables us to emulate the proof technique of Theorem 2.4, is that

• $\widetilde V^\beta_\lambda$ is locally Lipschitz on $\mathbb{R}\times\mathbb{R}^n$.

The idea of using the quadratic inf-convolution in order to construct near optimal strategies goes back to Subbotin and his coworkers, where it was employed in a differential games context; see, e.g., Subbotin [51].

Since $S$ is compact in the present case, we have

$$\widetilde V^\beta_\lambda(t,x) := \min_{(t^{\prime},x^{\pri... ...\lambda \Vert(t^{\prime},x^{\prime})-(t,x)\Vert ^2 \right \}.$$ (3.14)

Denote

$$m_{u} := \max_{(t,x)\in [0,T]\times S}\{\ell(x)+\beta (T-t)\} = \max_{x\in S} \ell(x) + \beta T$$

and

$$m_{\ell} := \min_{(t,x)\in [0,T]\times S}\widetilde V^\beta(... ... \min_{(t,x)\in [0,T]\times S}\widetilde V_\lambda^\beta(t,x).$$

These extrema are attained due to the compactness of $S$, continuity of $% \ell$, lower semicontinuity of $\widetilde V^\beta$, and continuity of $% \widetilde V^\beta_\lambda$. The fact that the second equality involving $% m_\ell$ holds for any $\lambda >0$ is evident from (3.14). Note also that

$$\sup_{(t,x)\in [0,T]\times S}\widetilde V^\beta_\lambda(t,x)... ...sup_{(t,x)\in [0,T]\times S}\widetilde V^\beta(t,x) \leq m_u.$$ (3.15)

Suppose $\partial _{P}\widetilde{V}_{\lambda }^{\beta }(t,x)\neq \phi$ at some $(t,x)\in \mathbb{R}\times \mathbb{R}^{n}$. Basic proximal analytic facts about the quadratic inf-convolution (see Clarke, Ledyaev, and Wolenski [17] as well as the exposition in [20]) are that

• there is a unique minimizer $(\bar t^{\prime},\bar x^{\prime})$ in (3.14);

• $\partial _{P}\widetilde{V}_{\lambda }^{\beta }(t,x)$ is a singleton and is contained in $\partial _{P}\widetilde{V}^{\beta}(\bar t^{\prime}, \bar x^{\prime})$.

In addition, we will require some elementary lemmas.

Lemma 3.3   Let $\rho >0$ be given, and let $(t,x)\in \{[0,T]\times S\}+\rho B_{n+1}$. Then for any minimizer $(\bar t^{\prime},\bar x^{\prime})$ in (3.14), one has

$$% latex2html id marker 663\Vert (\bar{t}^{\prime },\bar{x}... ...ert \leq \sqrt{\frac{% m_{u}-m_{\ell }}{\lambda }+\rho ^{2}}.$$ (3.16)

We now fix $\hat T \in (0,T)$; subsequently it is required that $T-\hat T$ be taken sufficiently small. The next lemma follows easily from the previous one and (3.11).

Lemma 3.4   There exists $\kappa >0$ such that $\rho <\kappa$ and $\lambda >1/\kappa$ together imply

$$\bar h_\varepsilon(x,\theta ,\zeta )\leq -\beta \quad \foral... ...\quad \forall \,(t,x)\in \{[0,\hat T]\times S\}+\rho B_{n+1}.$$ (3.17)

We now introduce notation for the sublevel sets of $\widetilde V^\beta$ and $% \widetilde V_\lambda^\beta$

$$% latex2html id marker 1968\widetilde S^\beta(b) := \{(t,x... ... \mathbb{R}\times\mathbb{R}^n:\widetilde V^\beta(t,x)\leq b\},$$

$$% latex2html id marker 1970\widetilde S_\lambda^\beta(b) :... ...R}\times\mathbb{R}^n:\widetilde V^\beta_\lambda (t,x)\leq b\}.$$

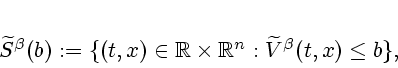
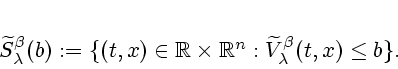
We shall also require the following lemma, which asserts how the sublevel sets of $\widetilde V^\beta$ are approximated by those of its quadratic inf-convolution. (We denote the Hausdorff metric by ``haus''.)

Lemma 3.5   For any $c\geq m_{\ell }$, one has

$$% latex2html id marker 690{\rm haus}\left[ \widetilde{S}_{... ...^{\beta }(c)\right] \leq \sqrt{\frac{c-m_{\ell }}{\lambda }}.$$ (3.18)

Now fix $\eta >0$; we will not require the smallness of this parameter. It is easy to see that for any $\beta$ and $\lambda$ one has

$$\widetilde{S}^{\beta }(m_{u}+\eta ) = [0,T]\times S;$$ (3.19)

then by (3.15) and the continuity of $\widetilde V^\beta_\lambda$,

$$% latex2html id marker 710[0,T]\times S \subset {\rm int} \{\widetilde S^\beta_\lambda(m_u+\eta)\}.$$ (3.20)

Let $\varepsilon^{\prime}$ be given. In view of the preceding lemma, it therefore follows that $\lambda$ can be taken large enough to guarantee

$$% latex2html id marker 715[0,T]\times S \subset {\rm int} ... ...epsilon^{\prime})B_{n+1} =: Q(T,\hat T,\varepsilon^{\prime}).$$ (3.21)

Then if $\varepsilon^{\prime}$ and $(T-\hat T)$ are taken sufficiently small in (3.21) with $\lambda$ increased as required, Lemma 3.4 implies

$$\bar h_{\varepsilon}(x,\theta,\zeta) \leq -\beta\quad \foral... ...x), ~~ \forall \, (t,x) \in Q(T,\hat T,\varepsilon^{\prime}).$$ (3.22)

This puts us in a position to adapt the general technique used in proving Theorem 2.4 to the function $\widetilde V^\beta_\lambda$ with $% \lambda$ chosen as above. For the given $\varepsilon$ in the statement of Theorem 3.2, the parameters $\varepsilon^{\prime}$ and $\beta$ are taken sufficiently small, $% \tilde T$ near $T$, and $T^{\prime}$ near $\tilde T$, in such a way that further estimates lead to the required conclusion. The idea of the proof is to use (3.21) and (3.22) in order to show that $x_\pi$ achieves appropriate nonincrease while never leaving the set ${\rm int} \{\widetilde S^\beta_\lambda(m_u+\eta)\}$; a shell based construction is employed, as described in connection with Theorem 2.4.

Remark 3.6    

1. When $S=\mathbb{R}^{n}$ (no state constraint) and the error functions $% p$ and $q$ are both zero (no measurement or external errors), the above result was proven in Nobakhtian and Stern [42] without enlarging the dynamics. (Euler polygonal arcs were employed in [42] as opposed to $\pi$-trajectories here; we need not dwell upon the distinction.) In that less general version of Theorem 3.2, (3.3) is replaced by the one-sided condition
   

   $$t_{i+1}-t_{i}\leq \delta ,\quad i=0,1,\ldots ,N_{\pi }-1.$$ (3.23)

   
   
   As was pointed out earlier, it is the presence of the state measurement error $p$ which necessitates the lower bound in (3.3) of Theorem 3.2.

   Berkovitz [6] provided a method of universal feedback construction for optimal control, quite different from those mentioned above, but one which also relies upon a nonsmooth Hamilton-Jacobi approach. In the context of the present article, Berkovitz's approach can be described as follows. Since the value function $V=V(t,x)$ of the problem is known to satisfy the generalized Hamilton-Jacobi inequality
   

   $$% latex2html id marker 755\min_{v\in f(x,U)}DV(t,x;1,v) = 0,\quad (t,x) \in (-\infty,T)\times \mathbb{R}^n,$$ (3.24)

   
   
   one approach (which is known to work when $V$ is smooth) is to consider a set-valued ``feedback map'' $U(t,x)$ such that
   

   $$f(t,x,U(t,x)) = argmin_{v\in f(x,U)} DV(t,x;1,v).$$ (3.25)

   
   
   One is then led to consider the differential inclusion
   

   $$\dot x \in f(x,U(t,x)).$$ (3.26)

   
   
   It transpires that under the present hypotheses, any solution of this differential inclusion corresponds to an optimal trajectory of the optimal control problem. On the other hand, as is noted in [6], the multifunction $f(x,U(t,x))$ on the right-hand-side of (3.26) in general lacks sufficient regularity (most notably, convexity, compactness, and upper semicontinuity) for the existence of solutions to hold in general, or, for that matter, for discretized solution procedures to be applicable. However, it is known (see Subbotina [53]) that under sufficient smoothness of the dynamics $f$ and cost functional $\ell$, the feedback map $% U(t,x)$ is compact valued and upper semicontinuous, but convexity of $% f(x,U(t,x))$ can still fail.

   An approach to feedback construction related to [6] and [53] was undertaken by Cannarsa and Frankowska in [8]; in that work, additional conditions on the cost functional and dynamics were given which provide the requisite regularity in Berkovitz's original procedure, namely, smoothness of $V$.

   In Rowland and Vinter [45], a modification of Berkovitz's method is given which overcomes the lack of regularity of $V$ without imposing extra conditions. Rowland and Vinter provided a discretization procedure (but not a feedback law) which in the limit produces an optimal trajectory for any initial phase.

2. If $V$ is known, then a special case of Theorem 4.8.1 of [20] (which first appeared as Theorem 10.1 in [14]) provides a proximal aiming method for constructing a feedback, such that all its limiting discretized (in this case, Euler polygonal arcs) solutions are optimal (that is, $\varepsilon =0$), for a given initial data pair $% (\tau ,\alpha )$. Actually, the invariance-based proof shows that a somewhat better result holds: the feedback produces optimal limit solutions for any initial data in the set
   
   $$% latex2html id marker 2052S:=\{(\tau ^{\prime },\alpha ^{... ...}:V(\tau ^{\prime },\alpha ^{\prime })\leq V(\tau ,\alpha )\}.$$
   
   
   The universality property of the feedback produced in Theorem 3.2 is an important distinction, and in a sense, the weakening of ``optimal'' to ``$% \varepsilon$-optimal for any given $\varepsilon > 0$'' in Theorem 3.2 can be viewed as the price paid for universality, albeit a small one in any practical sense. Whether this price is truly unavoidable is an open question, since we do not at present have a counterexample to the $% \varepsilon =0$ case (either for $\pi$-trajectories or for limiting $\pi$-trajectories). On the other hand, Subbotina [52] (see also Krasovskii and Subbotin [35]) has provided an example of a fixed duration differential game which does not possess a universal saddle point, under hypotheses which imply the existence of a saddle point for each individual startpoint.

3. In Theorem 10.2 of [14], a sufficient condition is given for the existence of a universal $\varepsilon$-optimal feedback, in the classical ordinary differential equations (as opposed to the discretized or limiting discretized) solution sense. This condition requires finding a Lipschitz semisolution to a strict Hamilton-Jacobi inequality, but with the proximal subdifferential $\partial _{P}V$ replaced by the generalized subdifferential $\partial _{C}V$ of Clarke, which is in general a larger object than the $P$-subdifferential. Because of this, the value function in general does not satisfy this condition, so there is the difficulty of finding an appropriate semisolution if one seeks to apply this result.

4. In Clarke, Ledyaev, and Subbotin [15], a proximal analytic method is given for constructing universal $\varepsilon$-optimal feedback controls in differential games of pursuit, in the Krasovskii-Subbotin framework; see also [16]. This work is related to that of Garnysheva and Subbotin [27], [26], who constructed suboptimal discontinuous feedback by using what they called aiming at ``quasi-gradients''; see also Subbotin [51]. The feedbacks in [15] were constructed with the aid of the quadratic inf-convolutions of a not necessarily continuous proximal semisolution to a Hamilton-Jacobi inequality; this lack of continuity is a natural feature of the value function in time-optimal and pursuit problems, as it is in the fixed duration state constrained control problem considered above.

5. For maximum principle based approaches to the general problem of optimal control in the presence of state constraints, see Ferreira, Fontes, and Vinter [23] as well as Vinter and Zheng [55].

3.1 A strengthening under additional assumptions on $S$

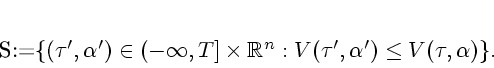
Let us now posit the following additional geometric assumptions on the state constraint set $S$:

(S1)

$S$ is compact.

(S2)

$S$ is wedged. (This means that at each point $x\in S$, the Clarke normal cone $N^C_S(x)$ is pointed.)

(S3)

$S$ is regular. (This is the condition that at every point in $S$, the Clarke tangent cone $T_S^C(x)$ agrees with the Bouligand or D-tangent cone

$$% latex2html id marker 2092T_S^D(x) := \{v\in \mathbb{R}^n : Dd_S(x;v)=0\}$$

at each $x\in S$.)

(S4)

The following ``strict inwardness'' condition holds: there exists $\kappa >0$ such that

$$h(x,\zeta )\leq -\kappa \Vert \eta \Vert \quad \forall \,\zeta \in N_{S}^{P}(x),\quad \forall \,x\in S.$$ (3.27)

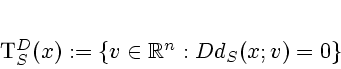
In Clarke, Rifford, and Stern [18], the following result is proven by means of a state constrained tracking lemma.

We denote $\hat S := {\rm cl}[{\rm comp} (S)]$, and for $r > 0$, we denote the r-inner approximation of $S$ by

$$S_r := \{x: d_{\hat S}(x) \geq r\}.$$

Inner approximations of this type were extensively studied in Clarke, Ledyaev, and Stern [19]. In [18], the following result is given.

Proposition 3.7   Let $(S1)-(S4)$ hold. Let $t_{0}\in (-\infty ,T)$ and $\varepsilon > 0$ be specified. Then for $r > 0$ taken sufficiently small, there exists a feedback $% k_{r}$ along with positive numbers $\delta _{0}^{r}$ and $E_{q}^{r}$ such that, for every $\delta \in (0,\delta _{0}^{r})$ there exists $E_{p}(\delta )>0$ as follows: for every initial phase

$$(\tau ,\alpha )\in \lbrack t_{0},T]\times S_{r}$$ (3.28)

and any partition $\pi$ of $[\tau ,T]$ with

$$\frac{\delta }{2}\leq t_{i+1}-t_{i}\leq \delta ,\quad i=1,2,\ldots ,N_{\pi }-1,$$ (3.29)

the error bounds

$$\Vert p(t_{i})\Vert \leq E_{p}(\delta ),\quad i=0,1,\ldots ,N_{\pi }-1,$$ (3.30)

and

$$\Vert q\Vert _{\infty }\leq E_{q}^{r}$$ (3.31)

imply that the associated $\pi$-trajectory $x_{\pi }$ of $(\ref{de1})$ satisfying $x_{\pi }(\tau )=\alpha$ also satisfies

$$\ell (x_{\pi }(T))\leq V(\tau ,\alpha )+\varepsilon$$ (3.32)

and

$$x_{\pi }(t)\in S\quad \forall \,t\in \lbrack \tau ,T].$$ (3.33)

In other words, under the strengthened hypotheses on $S$, for a given tolerance $\varepsilon > 0$, if one considers any sufficiently tight inner approximation $S_r$ of $S$, there exists a robust feedback $k_r$ effective universally for initial phases in $[t_0,T]\times S_r$, such that for each such initial phase, the $\pi$-trajectory produced (for the original, i.e. not enlarged dynamics) is $\varepsilon$-optimal and remains in $S$. This is in contrast to Theorem 3.2, where the $% \pi$-trajectory only remains $\varepsilon$-near $S$ under enlarged dynamics.

Further results,including a Hamilton-Jacobi characterization of the state constrained value, are to appear in [18].