

Next: 2 Stabilizability
Up: clark
Previous: clark
Consider a control system
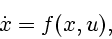 |
(1.1) |
where controls are Lebesgue measurable functions
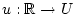 , with the control constraint set
, with the control constraint set
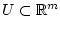 being compact. The following hypotheses will remain in
effect throughout:
being compact. The following hypotheses will remain in
effect throughout:
- (F1)
-
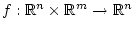 is continuous
and locally Lipschitz in the state variable
is continuous
and locally Lipschitz in the state variable 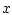 ; that is, for each
bounded subset
; that is, for each
bounded subset 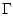 of
of
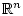 , there exists
, there exists 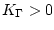 such that
such that
whenever 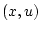 and
and 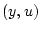 are in
are in
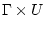 .
.
- (F2)
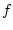 satisfies the linear growth condition
satisfies the linear growth condition
for some positive constants 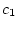 and
and 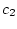 .
.
Under these assumptions, for each control function 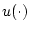 and
each initial phase
and
each initial phase
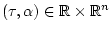 ,
there exists a unique solution
,
there exists a unique solution
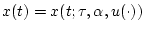 on
on
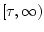 satisfying
satisfying
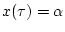 . Although the
preceding hypotheses on the dynamics can be relaxed in certain
results to follow, for ease of exposition we will retain the above
assumptions throughout the entire article.
. Although the
preceding hypotheses on the dynamics can be relaxed in certain
results to follow, for ease of exposition we will retain the above
assumptions throughout the entire article.
A central issue in control theory is the construction of feedback control
laws which achieve a desired behavior of the control system (1.1) in a
manner which is both
- universal: the desired behavior achieved by the feedback holds
for all initial phases in a prescribed set
and
- robust: the feedback is effective in the presence of external
disturbance and state measurement error.
Two general types of feedback control problems will be considered in this
article; these can be described in very general terms as follows:
Some articles and general references which are relevant to the present work,
but which are not directly referenced below as are others, include [36], [48], [39], [40], [54], [2],
[3], [21], [25], [28], [29], [30], and [43] .
Our approach in this survey is to use the constructions employed
in solving the stabilizability problem, where an infinitesimal
decrease property of a nonsmooth control Lyapunov function is
utilized, in designing feedbacks in the optimal control problem;
there, the infinitesimal decrease of the value function is employed
in an analogous way.
Even in very simple cases, one cannot expect the existence of universal
feedback laws 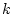 which are continuous, this being the minimal condition for
the classical existence theory of ordinary differential equations to apply
to (1.2) or (1.3). This inadequacy of continuous feedback is
well illustrated via the following two examples.
which are continuous, this being the minimal condition for
the classical existence theory of ordinary differential equations to apply
to (1.2) or (1.3). This inadequacy of continuous feedback is
well illustrated via the following two examples.
Example 1.1 A famous result of Brockett [
7] asserts that when
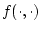
is assumed to be
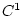
-smooth,
stabilizability by means of a continuous feedback law implies the
covering condition that the image of
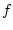
contains an open
neighborhood of the origin; for an elegant degree-theory-based
proof of this fact, attributed to R. D. Nussbaum ca. 1982, see
Sontag [
50]. Brockett provided the following
3-dimensional example, known as the ``nonholonomic integrator,''
showing that the covering condition can fail for asymptotically
controllable bilinear systems:
The asymptotic controllability is verifiable by an ad hoc argument; the
failure of the covering condition is easy to check.
Remark 1.2 By a
Filippov solution (see [
24]) of
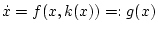
is meant an absolutely continuous function
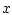
solving the differential inclusion
where the second intersection is
taken over all subsets
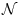
of
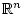
with Lebesgue
measure zero. The belief that the Filippov solution concept was
adequate for using discontinuous feedback laws to achieve
stabilizability was negated by a result of Ryan [
46]; see
also Coron and Rosier [
22]. On the other hand, the
problem of finding an adequate solution concept for discontinuous
feedback under which asymptotic controllability and feedback
stabilization are equivalent was first solved by Clarke, Ledyaev,
Sontag, and Subbotin [
13]. There,
as in the present exposition, a discretized solution concept was employed.
The main idea in the next example goes back to Barabanova and
Subbotin [4], [5]; see also Krasovskii
and Subbotin [35], [34] as well as Clarke,
Ledyaev, and Subbotin [16].
Example 1.3 Consider the optimal control problem with dynamics
where
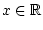
,
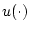
is valued in
![$U=[-1,1]$](img43.gif)
, and
where it is desired to minimize the endpoint cost functional
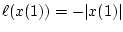
. First consider any continuous feedback
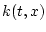
which is Lipschitz in
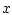
and such that solutions of (
1.3) are defined on
![$[0,1]$](img46.gif)
for every
![% latex2html id marker 1336
$%
\alpha \in \lbrack -1,1]$](img47.gif)
. Then there is a unique solution
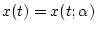
of
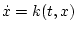
on
![$[0,1]$](img46.gif)
for each such
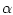
. Now note that the function
![$Q:[-1,1]\rightarrow \lbrack
-1,1]$](img51.gif)
given by
is continuous and, therefore, has a fixed point
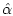
by
virtue of Brouwer's fixed point theorem. Furthermore,
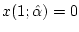
. Now consider the discontinuous feedback law
Upon substituting into the dynamics, we see that for
any
![$\alpha \in \lbrack -1,1]$](img56.gif)
, the resulting trajectory satisfies
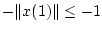
. This argument can be extended, by
approximation, to the case of merely continuous
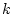
. Therefore,
given any continuous feedback
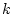
, there is at least one initial
phase
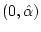
with
![$\hat{\alpha}\in \lbrack -1,1]$](img59.gif)
,
such that the above discontinuous feedback produces a better
outcome than the continuous one. Hence, there does not exist a
continuous feedback which is optimal universally for initial
phases in the set
![$\{0\}\times \lbrack -1,1]$](img60.gif)
. (Of course, it is
not always possible to obtain a classical solution to the
differential equation
when the feedback
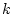
is
discontinuous, since the existence theory of ordinary differential
equations can break down, but in the present example, this
difficulty does not occur.)
We now pause to fix our notation from nonsmooth analysis. Our main general
references for the basic results we will employ from this subject are
Clarke, Ledyaev, Stern, and Wolenski [20]; see also [14],
Clarke [9], [10], and Loewen [41].
The Euclidean norm is denoted
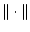 , and
, and
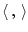 is the usual inner product. The open unit ball in
is the usual inner product. The open unit ball in
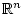 is denoted
is denoted 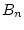 . For a set
. For a set
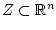 , we denote by
, we denote by
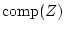 ,
, 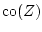 ,
, 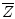 ,
, 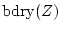 and
and 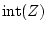 the
complement, convex hull, closure, boundary, and interior of
the
complement, convex hull, closure, boundary, and interior of 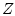 , respectively.
, respectively.
Let 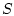 be a nonempty subset of
be a nonempty subset of
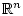 . The distance of a point
. The distance of a point 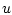 to
to 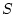 is given by
is given by
The metric projection of 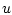 on
on 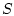 is denoted
is denoted
If 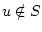 and
and
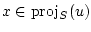 , then the vector
, then the vector 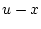 is called a
perpendicular to
is called a
perpendicular to 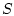 at
at 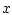 . The cone consisting of all
nonnegative multiples of these perpendiculars is denoted
. The cone consisting of all
nonnegative multiples of these perpendiculars is denoted
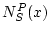 and is referred
to as the proximal normal cone (or P-normal cone) to
and is referred
to as the proximal normal cone (or P-normal cone) to 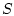 at
at 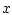 . If
. If
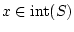 or no perpendiculars to
or no perpendiculars to 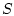 exist at
exist at 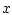 , then we set
, then we set
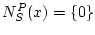 . Observe that the P-normal cone is a local
construction, since as can readily be shown,
. Observe that the P-normal cone is a local
construction, since as can readily be shown,
Let
![% latex2html id marker 1438
$g:\mathbb{R}^n\rightarrow (-\infty,\infty]$](img85.gif) be an extended real
valued function which is lower semicontinuous; that is, for each
be an extended real
valued function which is lower semicontinuous; that is, for each
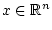 ,
,
a property
equivalent to closedness of the epigraph of 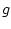 ,
,
We denote the effective domain of 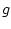 by
by
A vector
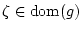 is said to be a proximal subgradient (or P-subgradient)
of
is said to be a proximal subgradient (or P-subgradient)
of 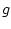 at a point
at a point
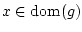 provided that
provided that
The set of all such vectors is called the P-subdifferential of 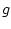 at
at 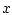 , denoted
, denoted
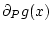 . One can show that
. One can show that
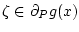 iff there exists
iff there exists 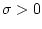 such that
such that
for all  near
near 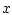 , and that
, and that
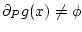 for a
dense subset of
for a
dense subset of 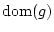 (where we adopt the convention that
(where we adopt the convention that
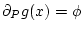 when
when
 ).
).
The limiting normal cone (or L-normal cone) to 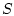 at
at 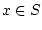 is defined to be the set
is defined to be the set
The L-normal cone leads to a corresponding L-subdifferential set
for 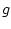 :
:
the members of which are called L-subgradients.
The Clarke normal cone (or C-normal cone) to 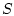 at
at 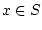 is defined by
is defined by
and the corresponding subdifferential for 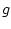 at
at 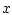 is
is
The lower Dini derivate of 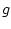 at
at 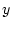 in the direction
in the direction 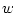 is
is
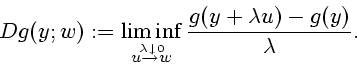 |
(1.4) |
In case 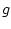 is locally Lipschitz, one has the simplification
is locally Lipschitz, one has the simplification
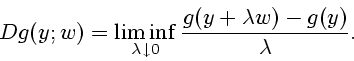 |
(1.5) |
The discretized solution concept we will work with includes a
state measurement error 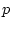 and an external disturbance
and an external disturbance 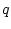 in a
perturbed version of (1.1) under a (generally discontinuous)
feedback
in a
perturbed version of (1.1) under a (generally discontinuous)
feedback 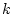 , modeled by
, modeled by
Here
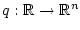 is a bounded measurable function,
but no measurability assumptions are made on
is a bounded measurable function,
but no measurability assumptions are made on
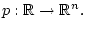 Let
Let
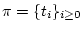 be a partition of
be a partition of
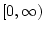 , by which is meant a countable, strictly increasing
sequence
, by which is meant a countable, strictly increasing
sequence 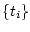 with
with 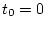 and
and
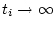 as
as 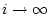 . Let an initial phase
. Let an initial phase
![% latex2html id marker 1538
$(\tau ,\alpha )\in (-\infty
,T]\times \mathbb{R}^{n}$](img123.gif) be specified. The associated
be specified. The associated 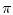 -trajectory
-trajectory 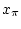 is the curve
is the curve 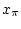 satisfying
satisfying
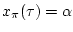 and
and
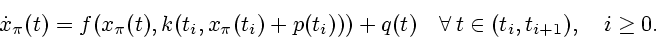 |
(1.6) |
Note that 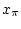 is the unique solution on
is the unique solution on 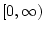 of the
differential equation
of the
differential equation
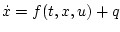 satisfying
satisfying
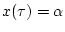 , with a piecewise constant control function
, with a piecewise constant control function 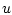 determined by the feedback
determined by the feedback 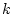 and the measurement error
and the measurement error 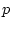 . This
solution procedure, which involves discretizing the feedback
control law
. This
solution procedure, which involves discretizing the feedback
control law  via ``closed loop system sampling,'' is the same
as the ``step-by-step'' solution concept employed by Krasovskii
and Subbotin [34], [35] in differential game
theory.
via ``closed loop system sampling,'' is the same
as the ``step-by-step'' solution concept employed by Krasovskii
and Subbotin [34], [35] in differential game
theory.


Next: 2 Stabilizability
Up: clark
Previous: clark
2003-08-05
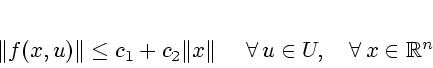
![]() and
each initial phase
and
each initial phase
![]() ,
there exists a unique solution
,
there exists a unique solution
![]() on
on
![]() satisfying
satisfying
![]() . Although the
preceding hypotheses on the dynamics can be relaxed in certain
results to follow, for ease of exposition we will retain the above
assumptions throughout the entire article.
. Although the
preceding hypotheses on the dynamics can be relaxed in certain
results to follow, for ease of exposition we will retain the above
assumptions throughout the entire article.
![]() which are continuous, this being the minimal condition for
the classical existence theory of ordinary differential equations to apply
to (1.2) or (1.3). This inadequacy of continuous feedback is
well illustrated via the following two examples.
which are continuous, this being the minimal condition for
the classical existence theory of ordinary differential equations to apply
to (1.2) or (1.3). This inadequacy of continuous feedback is
well illustrated via the following two examples.
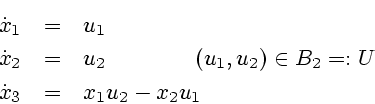
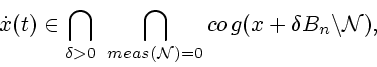
![\begin{eqnarray*}
\dot{x} = u,\quad t\in [0,1], \\ x(0) = \alpha ,
\end{eqnarray*}](img41.gif)
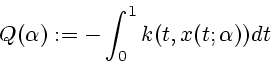
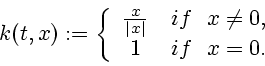
![]() , and
, and
![]() is the usual inner product. The open unit ball in
is the usual inner product. The open unit ball in
![]() is denoted
is denoted ![]() . For a set
. For a set
![]() , we denote by
, we denote by
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() the
complement, convex hull, closure, boundary, and interior of
the
complement, convex hull, closure, boundary, and interior of ![]() , respectively.
, respectively.
![]() be a nonempty subset of
be a nonempty subset of
![]() . The distance of a point
. The distance of a point ![]() to
to ![]() is given by
is given by
![]() on
on ![]() is denoted
is denoted
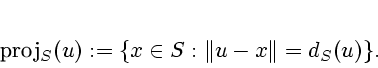
![]() be an extended real
valued function which is lower semicontinuous; that is, for each
be an extended real
valued function which is lower semicontinuous; that is, for each
![]() ,
,
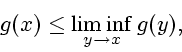
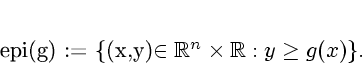
![]() by
by
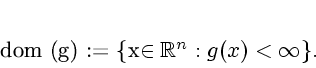
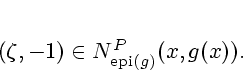
![]() at
at ![]() , denoted
, denoted
![]() . One can show that
. One can show that
![]() iff there exists
iff there exists ![]() such that
such that
![]() at
at ![]() is defined to be the set
is defined to be the set
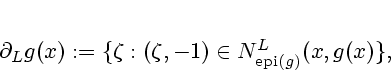
![]() at
at ![]() is defined by
is defined by
![\begin{displaymath}
% latex2html id marker 1498N^C_S(x) := \overline {{\rm co}} [N^L_S(x)],
\end{displaymath}](img107.gif)
![]() at
at ![]() is
is
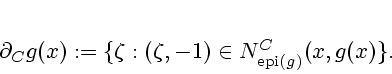
![]() at
at ![]() in the direction
in the direction ![]() is
is
![]() and an external disturbance
and an external disturbance ![]() in a
perturbed version of (1.1) under a (generally discontinuous)
feedback
in a
perturbed version of (1.1) under a (generally discontinuous)
feedback ![]() , modeled by
, modeled by