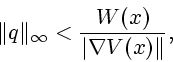

Next: 3 Fixed duration state
Up: clark
Previous: 1 INTRODUCTION
Definition 2.1 The control system (
1.1) is
globally asymptotically
controllable (or GAC) provided that there exists a nonincreasing function
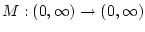
such that
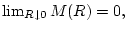
and a function
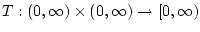
such that the following holds. Let
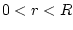
be given. Then,
given any
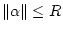
, there exists a control function so
that the associated trajectory which satisfies
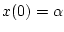
also
satisfies
- (i)
-
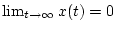 ;
;
- (ii)
-
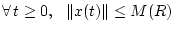 ;
;
- (iii)
-
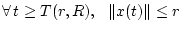 .
.
We say that a function
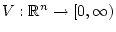 is positive definite if
is positive definite if 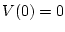 and
and 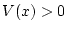 whenever
whenever 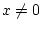 . Also,
. Also, 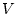 is
said to be proper provided that
is
said to be proper provided that
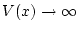 as
as
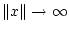 .
.
Definition 2.2 A
control Lyapunov pair is a pair of continuous, positive
definite functions
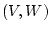
, with
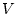
also proper, such that for each
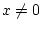
one has the infinitesimal decrease condition
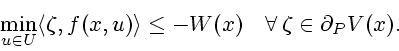 |
(2.1) |
We refer to the
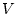
in a control Lyapunov pair as a
control Lyapunov
function (or CLF).
The infinitesimal decrease condition is equivalent to one in Dini derivate
terms, which has been used by several authors in characterizing nonsmooth
CLF's; see Sontag [47] as well as Sontag and Sussman [49]. This Dini formulation is
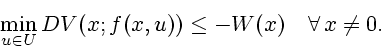 |
(2.2) |
The equivalence of (2.1) and (2.2) is due to a deep
theorem of Subbotin [51], which links the proximal and directional
generalized solution concepts for partial differential equations. An
alternate proof of Subbotin's theorem was derived by Clarke and Ledyaev via
a generalized mean value inequality [11]; see also [20].
Recently, Rifford [44] proved the following result.
Theorem 2.3
The control system 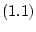 is GAC iff there exists a CLF
which is locally Lipschitz on
is GAC iff there exists a CLF
which is locally Lipschitz on
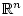 .
.
The above theorem extends an important result of [47]
(see also [49]) where the CLF produced is only
continuous. In this regard, Theorem 2.3 provides an
answer to a conjecture attributed to Sontag and Sussman.
Furthermore, Theorem 2.3 extends a result of Clarke,
Ledyaev, Rifford, and Stern [12], where the CLF produced
is locally Lipschitz, but only on the complement of a ball around
the origin.
Theorem 2.3 and Theorem 3 of [12] yield a
general result on robust stabilization. The asserted stabilization
is framed in terms of the sublevel sets of a CLF. We introduce the
following sublevel set notation for given 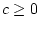 :
:
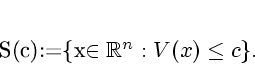
Remark 2.5
- In view of the nature of the CLF
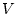 , the preceding result
implies that for any
, the preceding result
implies that for any 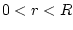 , there exists a feedback defined on a
neighborhood of
, there exists a feedback defined on a
neighborhood of 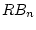 which stabilizes every initial point in the ball
which stabilizes every initial point in the ball 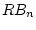 to the ball
to the ball 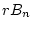 in a robust manner.
in a robust manner.
- The feedback
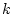 is constructed via a technique dubbed proximal aiming in [14] and [20]. This is a
projective method akin to the extremal aiming concept of
Krasovskii and Subbotin in differential game theory
[34], [35]. The feedback
is constructed via a technique dubbed proximal aiming in [14] and [20]. This is a
projective method akin to the extremal aiming concept of
Krasovskii and Subbotin in differential game theory
[34], [35]. The feedback 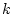 will now be
described in rough terms.
will now be
described in rough terms.
In view of the continuity of 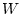 , given
, given 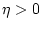 , there exists
, there exists 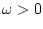 such that
such that
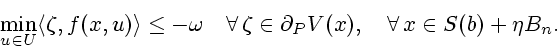 |
(2.9) |
Since 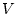 is Lipschitz on
is Lipschitz on
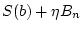 (we denote this Lipschitz rank
by
(we denote this Lipschitz rank
by 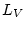 ) and
) and 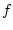 is continuous, it follows that (2.9) is equivalent
to
is continuous, it follows that (2.9) is equivalent
to
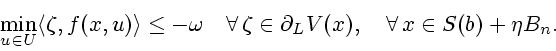 |
(2.10) |
For appropriately defined positive integer 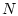 and positive constants
and positive constants 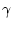 and
and 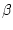 , one considers a family of ``shells''
, one considers a family of ``shells''
for
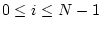 (along with specialized definitions for
(along with specialized definitions for
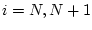 ). It can be arranged that the family is disjoint.
). It can be arranged that the family is disjoint.
Let
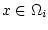 (
(
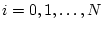 ) and choose
) and choose
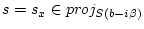 . Then the construction implies
. Then the construction implies 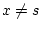 , and by
definition,
, and by
definition,
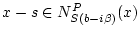 . A nonsmooth analysis argument
then yields the existence of
. A nonsmooth analysis argument
then yields the existence of 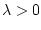 such that
such that
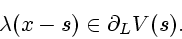 |
(2.11) |
We emphasize that in establishing (2.11), the Lipschitz
nature of 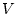 is crucial. In [13], where a nonrobust
version of Theorem 2.4 was proven, only a continuous
CLF was available, and a different proof technique was employed
(involving quadratic inf-convolutions, also required in the next
section).
is crucial. In [13], where a nonrobust
version of Theorem 2.4 was proven, only a continuous
CLF was available, and a different proof technique was employed
(involving quadratic inf-convolutions, also required in the next
section).
Now,
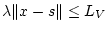 , and in view of
(2.10) there exists
, and in view of
(2.10) there exists 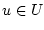 such that
such that
We then set 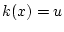 . It transpires that under the constructions
we have sketched, the
. It transpires that under the constructions
we have sketched, the 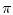 -trajectory emanating from
-trajectory emanating from 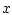 moves
towards
moves
towards 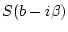 at a positive rate, with the process
resetting and continuing as
at a positive rate, with the process
resetting and continuing as 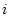 increases, with the
increases, with the 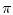 -trajectory meeting the requirements of the theorem.
-trajectory meeting the requirements of the theorem.
- The double sided bound on the meshsize in (2.3) says that
the partition
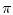 is ``reasonably uniform.'' The upper bound requires
that the step size be small enough to ensure stabilization, which is rather
natural. On the other hand, the lower bound may appear somewhat surprising.
Its purpose is to preclude a possible chattering phenomenon; each step must
be big enough to counteract the measurement error by means of the attractive
effect arising from the infinitesimal decrease property used in the
construction.
is ``reasonably uniform.'' The upper bound requires
that the step size be small enough to ensure stabilization, which is rather
natural. On the other hand, the lower bound may appear somewhat surprising.
Its purpose is to preclude a possible chattering phenomenon; each step must
be big enough to counteract the measurement error by means of the attractive
effect arising from the infinitesimal decrease property used in the
construction.
- The maximum allowable external disturbance error
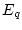 is
proportional to the quantity
is
proportional to the quantity 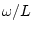 . That this is natural can
be seen heuristically by considering the (very) special case where
. That this is natural can
be seen heuristically by considering the (very) special case where
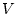 is smooth and
is smooth and 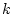 is a continuous feedback such that
is a continuous feedback such that
Then the perturbed system
is stabilized by this feedback if
which is a condition similar to a bound involving 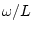 .
.
- Other types of error, such as a disturbance
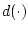 entering
into the dynamics as in
entering
into the dynamics as in
can easily be reduced to the case of an external disturbance
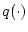 as in the preceding theorem, due to the continuity of
as in the preceding theorem, due to the continuity of
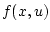 in the variable
in the variable 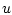 .
.
- Ledyaev and Sontag have approached the robustness question in
the presence of small measurement errors and an arbitrarily fast sampling
rate by alternate means in [37], [38].


Next: 3 Fixed duration state
Up: clark
Previous: 1 INTRODUCTION
2003-08-05
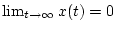 ;
;
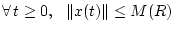 ;
;
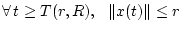 .
.
![]() is positive definite if
is positive definite if ![]() and
and ![]() whenever
whenever ![]() . Also,
. Also, ![]() is
said to be proper provided that
is
said to be proper provided that
![]() as
as
![]() .
.
![]() :
:
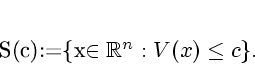
![]() , given
, given ![]() , there exists
, there exists ![]() such that
such that
![]() and positive constants
and positive constants ![]() and
and ![]() , one considers a family of ``shells''
, one considers a family of ``shells''
![]() (
(
![]() ) and choose
) and choose
![]() . Then the construction implies
. Then the construction implies ![]() , and by
definition,
, and by
definition,
![]() . A nonsmooth analysis argument
then yields the existence of
. A nonsmooth analysis argument
then yields the existence of ![]() such that
such that
![]() is crucial. In [13], where a nonrobust
version of Theorem 2.4 was proven, only a continuous
CLF was available, and a different proof technique was employed
(involving quadratic inf-convolutions, also required in the next
section).
is crucial. In [13], where a nonrobust
version of Theorem 2.4 was proven, only a continuous
CLF was available, and a different proof technique was employed
(involving quadratic inf-convolutions, also required in the next
section).
![]() , and in view of
(2.10) there exists
, and in view of
(2.10) there exists ![]() such that
such that
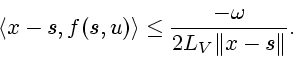
![]() . It transpires that under the constructions
we have sketched, the
. It transpires that under the constructions
we have sketched, the ![]() -trajectory emanating from
-trajectory emanating from ![]() moves
towards
moves
towards ![]() at a positive rate, with the process
resetting and continuing as
at a positive rate, with the process
resetting and continuing as ![]() increases, with the
increases, with the ![]() -trajectory meeting the requirements of the theorem.
-trajectory meeting the requirements of the theorem.