7. Продольное движение двузвенника

Покажем, как можно осуществить продольное движение двузвенника. Пусть в начальный момент двузвенник имеет прямолинейную форму
$(\theta= \alpha=0)$ и покоится (состояние $0$ на рис. 6).

1) Выполним медленное движение, повернув звено $OC_1$ на угол $\beta$. Двузвенник перейдет в состояние 1 на рис. 6, в котором $\alpha=\beta$.

2) Выполним быстрое движение, в результате которого угол $\alpha$ изменится от $\beta$ до $0$. Двузвенник станет снова прямолинейным, однако угол $\theta$ будет не равен нулю (состояние 2 на рис. 6; изменения угла $\theta$ на рис. 6 не показаны).

3) Выполним медленное движение, изменяя угол $\alpha$ от $0$ до $-\beta$. Двузвенник перейдет в состояние 3 на рис. 6.

4) Выполним быстрое движение, изменив угол $\alpha$ от $-\beta$ до $0$. Двузвенник перейдет в состояние 4 на рис. 6. Однако в этом состоянии, как можно показать, $y_0 \ne 0$. Чтобы перейти к состоянию с $y_0=0$, повторим предыдущие фазы движения, изменив их порядок. А именно, выполним последовательно движения 3, 4, 1, 2.

5) При помощи медленного движения изменим $\alpha$ от $0$ до $-\beta$. Двузвенник придет в состояние 5 на рис. 6.

6) Выполним быстрое движение, изменив $\alpha$ от $-\beta$ до $0$. Двузвенник перейдет в состояние 6 на рис. 6.

7) При помощи медленного движения изменим $\alpha$ от $0$ до $\beta$. Получим состояние 7 на рис. 6.

8) При помощи быстрого движения изменим $\alpha$ от $\beta$ до $0$. В результате получим состояние 8 на рис. 6, в котором, как можно показать, имеем $\Delta_0 y_0=0, \quad \Delta_0 \theta=0$.

Рис. 6. Продольное движение двузвенника.

Таким образом, состояние 8 отличается от исходного состояния $0$ лишь тем, что двухз венник продвинулся вдоль оси $x$. Можно показать, что его полное продольное смещение за цикл из восьми движений равно

$$\Delta_0x_0= {8m_0\ell \over m} \cos{\gamma \over 2} \sin{\b... ...} \sin{\beta-\gamma \over 2}, \quad m=m_0+m_1+m_2. \eqno (7.1)$$

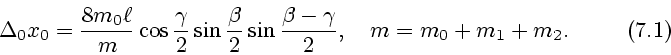
Здесь введены обозначения

$$\begin{array}{c} \gamma=\displaystyle {\beta\over 2}+{N\over... ...\ell^2+m_2b^2)+m_0m_2(\ell+b)^2]^{1/2}. \end{array}\eqno (7.2)$$

Показано,что справедливы неравенства $0<\gamma<\beta$. Таким образом, продольное смещение (7.1) положительно.

Описанный выше цикл из восьми движений можно повторять, осуществляя продольное перемещение двузвенника. Средняя скорость продольного движения равна $v_0=\Delta_0x_0(4T)^{-1}$, где $\Delta_0x_0$ определено соотношениями (7.1), (7.2). При этом длительность $T$ медленной фазы движения и угол $\beta$ должны удовлетворять неравенствам

$$\begin{array}{c} m_0 \ell (4\beta \ell T^{-2}+gk)\le m_2bgk,... ...eta(\beta^2+1)^{1/2}bT^{-2}]\le m_1bgk, \end{array}\eqno (7.3)$$

вытекающим из неравенств (3.5) и соотношений (3.1).

Поперечные движения двузвенника и его поворот вокруг вертикальной оси могут быть построены аналогично соответствующим движениям трехзвенника.