Чтобы получить любое заданное перемещение многозвенника по плоскости, достаточно построить его движения вдоль самого себя (продольное движение), поперек (боковое движение), а также вращение на месте. Эти движения сформируем из более простых движений, которые будем называть элементарными. При этом будем параллельно рассматривать случаи трехзвенника и двузвенника.
Каждое элементарное движение начинается и заканчивается в состоянии покоя
всего многозвенника. В случае трехзвенника, начальные и конечные
значения углов
![]() для каждого элементарного движения обозначим через
для каждого элементарного движения обозначим через
![]() и
и
![]() соответственно
соответственно ![]() .
.
Элементарные движения делятся на медленные и быстрые.
В медленных
движениях вращается одно или оба концевых звена, а корпус остается
неподвижным. Примем, что угловая скорость
![]() , концевых звеньев в медленном движении не меняет знака и справедливы
соотношения
, концевых звеньев в медленном движении не меняет знака и справедливы
соотношения
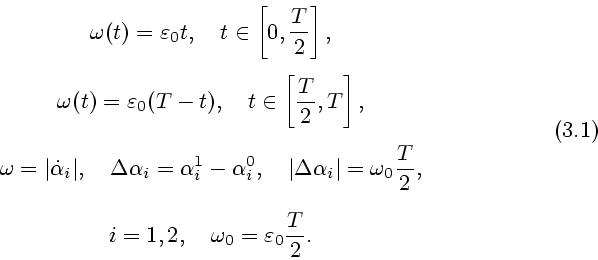
Здесь ![]() - время,
- время, ![]() - длительность медленного движения,
- длительность медленного движения,
![]() и
и ![]() - постоянные. Если в медленном движении
участвуют оба концевых звена, то они вращаются синхронно либо в одном и
том же, либо в противоположных направлениях, так что
- постоянные. Если в медленном движении
участвуют оба концевых звена, то они вращаются синхронно либо в одном и
том же, либо в противоположных направлениях, так что
Можно показать [8], что при медленном движении одного
или двух концевых звеньев корпус остается неподвижным, если
Если же концевые звенья вращаются в противоположные стороны, т.е.
имеет место знак "![]() " в (3.2), то (3.3) может быть заменено условием
" в (3.2), то (3.3) может быть заменено условием
Если концевые звенья вращаются достаточно медленно, т.е. ![]() и
и ![]() в (3.1) достаточно малы, то неравенство (3.4)
выполняется всегда, а неравенство (3.3) - при
в (3.1) достаточно малы, то неравенство (3.4)
выполняется всегда, а неравенство (3.3) - при
![]() .
.
В случае двузвенника, начальные и конечные значения угла ![]() для
элементарного движения обозначим через
для
элементарного движения обозначим через ![]() и
и ![]() соответственно. При медленных движениях вращается концевое звено
соответственно. При медленных движениях вращается концевое звено ![]() (хвост), а корпус остается неподвижным, причем всегда
(хвост), а корпус остается неподвижным, причем всегда ![]() ,
т.е. медленное движение начинается из прямолинейной конфигурации двузвенника.
Соотношения (3.1) остаются справедливыми для двузвенника, если в них всюду
опустить индекс
,
т.е. медленное движение начинается из прямолинейной конфигурации двузвенника.
Соотношения (3.1) остаются справедливыми для двузвенника, если в них всюду
опустить индекс ![]() .
.
При медленном движении корпус
двузвенника ![]() остается неподвижным, если выполняются два
неравенства
остается неподвижным, если выполняются два
неравенства
![\begin{displaymath}
\begin{array}{c}
m_0\ell(\varepsilon_0 \ell+gk) \le m_2bgk, ...
...on^2_0+\omega^4_0)^{1/2}b]
\le m_1bgk.
\end{array} \eqno (3.5)
\end{displaymath}](img66.gif)
Эти неравенства выводятся аналогично неравенствам (3.3) и (3.4).
Если выполнены условия ![]() и
и ![]() , то, как
нетрудно видеть, оба условия (3.5) выполняются, если концевое звено
вращается достаточно медленно, т.е.
, то, как
нетрудно видеть, оба условия (3.5) выполняются, если концевое звено
вращается достаточно медленно, т.е. ![]() и
и ![]() достаточно малы.
достаточно малы.
В быстрых движениях угловые скорости и ускорения достаточно велики, а
время движения ![]() мало по сравнению с временем
мало по сравнению с временем ![]() медленных движений.
При этом в случае трехзвенника, управляющие моменты
медленных движений.
При этом в случае трехзвенника, управляющие моменты ![]() и
и ![]() по величине много больше моментов сил трения, равных
по величине много больше моментов сил трения, равных ![]() , где
, где
![]() , и поэтому силы трения
можно не учитывать. Здесь по-прежнему выполняется условие (3.2), причем
имеет место один из трех случаев: 1)
, и поэтому силы трения
можно не учитывать. Здесь по-прежнему выполняется условие (3.2), причем
имеет место один из трех случаев: 1)
![]() и, кроме того, либо
и, кроме того, либо ![]() , либо
, либо ![]() 2)
2)
![]() 3)
3)
![]() . Эти случаи
будем называть быстрыми движениями типов 1, 2, 3 соответственно.
Закон изменения угловых скоростей в быстрых движениях несуществен.
. Эти случаи
будем называть быстрыми движениями типов 1, 2, 3 соответственно.
Закон изменения угловых скоростей в быстрых движениях несуществен.
В случае двузвенника, управляющий момент ![]() при быстрых движениях по
величине также много больше моментов сил трения
при быстрых движениях по
величине также много больше моментов сил трения ![]() , где
, где
![]() . Закон изменения угловой
скорости
. Закон изменения угловой
скорости
![]() здесь также несуществен, а угол
здесь также несуществен, а угол ![]() изменяется
от некоторого
изменяется
от некоторого ![]() до
до ![]() . Таким образом, быстрые движения
всегда заканчиваются при прямолинейной конфигурации двузвенника
. Таким образом, быстрые движения
всегда заканчиваются при прямолинейной конфигурации двузвенника ![]() .
.
Используя законы сохранения импульса и момента импульса, нетрудно подсчитать приращения за время быстрых движений линейных и угловых координат, определяющих положение и конфигурацию многозвенников.
В случае трехзвенника приращения переменных ![]() для быстрого
движения типа 1 равны
для быстрого
движения типа 1 равны
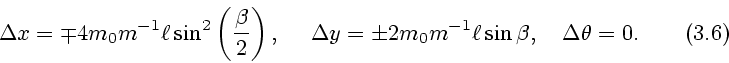
Аналогичные формулы получены для быстрых движений двузвенника.
Перейдем к формированию продольного, бокового и вращательного движений многозвенников из элементарных движений.