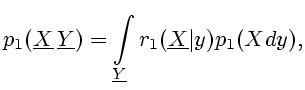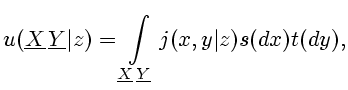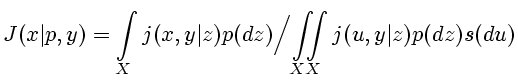

Next: 3 Случайные информационные множества
Up: ANANIEV
Previous: 1 Введение
Здесь мы
напомним и несколько обобщим известные результаты, которые изложим
в нужной нам интерпретации. В первом случае предполагается, что
случайные элементы отсутствуют. Тогда имеем уравнения
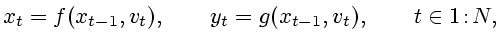 |
(2.1) |
с ограничениями
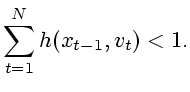 |
(2.2) |
Введем основное понятие в
детерминированном случае [1,2,3].
О п р е д е л е н и е 2.1. Информационным множеством
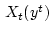 системы
(2.1) при ограничениях (2.2) назовем совокупность
элементов
системы
(2.1) при ограничениях (2.2) назовем совокупность
элементов 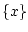 , для каждого из которых найдется начальное
состояние
, для каждого из которых найдется начальное
состояние 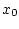 и последовательность
и последовательность 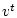 такие, что
неравенство
такие, что
неравенство
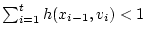 выполняется для
соответствующей траектории
выполняется для
соответствующей траектории 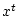 и
и 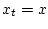 .
.
Информационные множества можно описать с помощью рекуррентно
определяемых функций
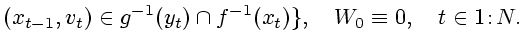 |
(2.3) |
Справедливо утверждение.
Теорема 2.2
Пусть сигнал 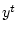 реализовался в
системе так, что были выполнены ограничения
реализовался в
системе так, что были выполнены ограничения (
2.2)
для
соответствующей траектории. Тогда информационные множества
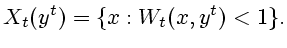 |
(2.4) |
являются
непустыми и аналитическими [
12]
. Функции
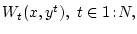 заданные на декартовом произведении
заданные на декартовом произведении 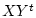 =
=
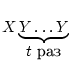 , со значениями в
, со значениями в
![$ [0,+\infty]$](img66.gif) , являются полуаналитическими снизу
, являются полуаналитическими снизу [
8]
.
Д о к а з а т е л ь с т в о. Пусть сигнал 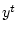 реализовался в системе при некоторых
элементах
реализовался в системе при некоторых
элементах
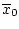 и
и
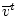 , и ограничения (2.2)
выполняются для соответствующей траектории
, и ограничения (2.2)
выполняются для соответствующей траектории
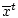 . Тогда
имеем
. Тогда
имеем
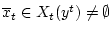 . Докажем равенство
(2.4). Если
. Докажем равенство
(2.4). Если
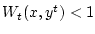 , то по определению функций
(2.3) получаем неравенство
, то по определению функций
(2.3) получаем неравенство
и при этом
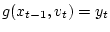 и
и
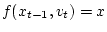 для некоторых
элементов
для некоторых
элементов
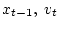 . Продолжая в том же духе, находим
последовательности
. Продолжая в том же духе, находим
последовательности
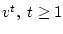 , и
, и
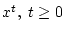 , для которых
выполняется неравенство
, для которых
выполняется неравенство
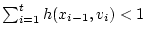 и
и
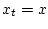 . Следовательно, правая часть равенства (2.4)
содержится в левой. Поскольку обратное включение очевидно, то
равенство доказано. Пусть
. Следовательно, правая часть равенства (2.4)
содержится в левой. Поскольку обратное включение очевидно, то
равенство доказано. Пусть
![$ l:XZ\to[0,+\infty]$](img78.gif) - некоторая
полуаналитическая снизу функция, заданная на произведении
борелевских пространств
- некоторая
полуаналитическая снизу функция, заданная на произведении
борелевских пространств 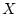 и
и 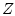 . Расширим ее на борелевское
множество
. Расширим ее на борелевское
множество
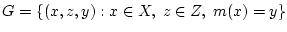 , где
, где 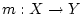 - некоторая борелевская функция, полагая
- некоторая борелевская функция, полагая
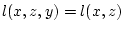 .
Далее согласно [8, Предл. 7.47] получаем, что функция
является
полуаналитической снизу. Здесь
.
Далее согласно [8, Предл. 7.47] получаем, что функция
является
полуаналитической снизу. Здесь 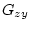 - сечение множества
- сечение множества
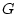 . Применяя индуктивно данные рассуждения к функциям
(2.3), получаем их полуаналитичность, а следовательно, и
аналитичность информационных множеств. Теорема доказана.
. Применяя индуктивно данные рассуждения к функциям
(2.3), получаем их полуаналитичность, а следовательно, и
аналитичность информационных множеств. Теорема доказана.
Поскольку множества 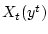 содержат истинные неизвестные
состояния, а элемент
содержат истинные неизвестные
состояния, а элемент
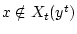 не может реализоваться в
системе (2.1) ни при каких элементах
не может реализоваться в
системе (2.1) ни при каких элементах 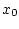 и
и 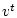 в силу
ограничений (2.2), то при данной информации
в силу
ограничений (2.2), то при данной информации 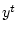 мы
вынуждены считать эти множества наилучшими оценками неизвестного
состояния. Если же по какой-либо причине необходимо выделить
точечную оценку фазового состояния, то нужен критерий для такого
выделения. Весьма часто за наилучшую оценку принимают
чебышевский центр информационного множества
мы
вынуждены считать эти множества наилучшими оценками неизвестного
состояния. Если же по какой-либо причине необходимо выделить
точечную оценку фазового состояния, то нужен критерий для такого
выделения. Весьма часто за наилучшую оценку принимают
чебышевский центр информационного множества 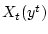 [1,2,3].
[1,2,3].
Отметим отдельно случай геометрических ограничений, а именно,
пусть
![$\displaystyle h(x,v)=\left\{\begin{array}{ll} 0,&(x,v)\in {\cal H},\\ [1ex] +\infty,&(x,v)\notin {\cal H},\end{array}\right.$](img87.gif) |
(2.5) |
где
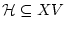 - аналитическое множество. Тогда ясно, что
- аналитическое множество. Тогда ясно, что
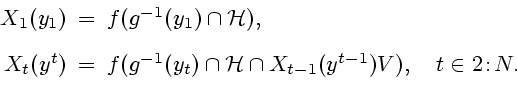 |
(2.6) |
Следует подчеркнуть, что множества 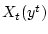 дают лишь
принципиальное решение задачи, которое в каждом конкретном
случае сопряжено со значительными трудностями при нахождении
нижних граней в (2.3) или пересечений множеств в
(2.6).
дают лишь
принципиальное решение задачи, которое в каждом конкретном
случае сопряжено со значительными трудностями при нахождении
нижних граней в (2.3) или пересечений множеств в
(2.6).
Перейдем ко второму случаю чисто случайных систем. Уравнения имеют
вид
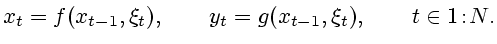 |
(2.7) |
Ограничения типа (1.3) здесь лишены
особого смысла и могут быть опущены по следующим причинам.
Во-первых, поскольку начальное состояние 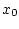 отнесено нами к
неопределенным факторам, то уже на первом шаге должна получиться
однозначная функция
отнесено нами к
неопределенным факторам, то уже на первом шаге должна получиться
однозначная функция 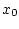 от
от 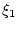 , а значит, однозначными
должны являться и функции
, а значит, однозначными
должны являться и функции
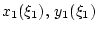 . Во-вторых,
неравенство (1.3) превращается тогда в ограничение на
реализации независимых случайных переменных
. Во-вторых,
неравенство (1.3) превращается тогда в ограничение на
реализации независимых случайных переменных 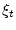 , что
неестественно. Итак, в данном случае имеем частично наблюдаемую
марковскую последовательность
, что
неестественно. Итак, в данном случае имеем частично наблюдаемую
марковскую последовательность
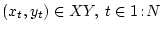 .
Решение задачи фильтрации для таких последовательностей известно и
изложено в необходимой нам общности, например, в упоминавшейся
книге [8]. Оно состоит в следующем. Определяется борелевское
стохастическое ядро
.
Решение задачи фильтрации для таких последовательностей известно и
изложено в необходимой нам общности, например, в упоминавшейся
книге [8]. Оно состоит в следующем. Определяется борелевское
стохастическое ядро
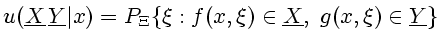 |
(2.8) |
и начальное
распределение
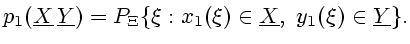 |
(2.9) |
Эти меры
определяются на произвольных борелевских прямоугольниках
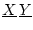 и однозначно продолжаются на
борелевскую
и однозначно продолжаются на
борелевскую 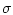 -алгебру
-алгебру 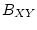 . Далее для произвольного
. Далее для произвольного 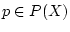 вводится ядро
вводится ядро
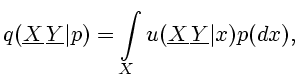 |
(2.10) |
которое в соответствии
с [8, Предл. 7.27] разлагается по формуле
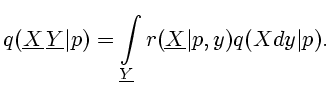 |
(2.11) |
Аналогично разлагаются и
начальные распределения
а затем рекуррентно определяются
меры
 |
(2.12) |
Отметим, что
мера
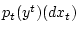 дает условное распределение неизвестного
состояния
дает условное распределение неизвестного
состояния 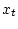 по данным измерения
по данным измерения 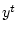 .
.
З а м е ч а н и е 2.3. Процесс вычисления мер (2.12) сводится к
байесовской процедуре пересчета плотностей в случае, когда ядра
(2.8) обладают плотностью, то есть
где 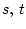 - некоторые борелевские
- некоторые борелевские
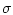 - конечные меры, а
- конечные меры, а 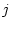 - неотрицательная борелевская
функция от трех переменных. Тогда в разложении (2.11) ядро
- неотрицательная борелевская
функция от трех переменных. Тогда в разложении (2.11) ядро
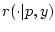 обладает плотностью
относительно меры
обладает плотностью
относительно меры 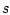 .
.


Next: 3 Случайные информационные множества
Up: ANANIEV
Previous: 1 Введение
2003-06-05
![]() системы
(2.1) при ограничениях (2.2) назовем совокупность
элементов
системы
(2.1) при ограничениях (2.2) назовем совокупность
элементов ![]() , для каждого из которых найдется начальное
состояние
, для каждого из которых найдется начальное
состояние ![]() и последовательность
и последовательность ![]() такие, что
неравенство
такие, что
неравенство
![]() выполняется для
соответствующей траектории
выполняется для
соответствующей траектории ![]() и
и ![]() .
.
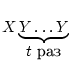 , со значениями в
, со значениями в
![]() реализовался в системе при некоторых
элементах
реализовался в системе при некоторых
элементах
![]() и
и
![]() , и ограничения (2.2)
выполняются для соответствующей траектории
, и ограничения (2.2)
выполняются для соответствующей траектории
![]() . Тогда
имеем
. Тогда
имеем
![]() . Докажем равенство
(2.4). Если
. Докажем равенство
(2.4). Если
![]() , то по определению функций
(2.3) получаем неравенство
, то по определению функций
(2.3) получаем неравенство
![]() содержат истинные неизвестные
состояния, а элемент
содержат истинные неизвестные
состояния, а элемент
![]() не может реализоваться в
системе (2.1) ни при каких элементах
не может реализоваться в
системе (2.1) ни при каких элементах ![]() и
и ![]() в силу
ограничений (2.2), то при данной информации
в силу
ограничений (2.2), то при данной информации ![]() мы
вынуждены считать эти множества наилучшими оценками неизвестного
состояния. Если же по какой-либо причине необходимо выделить
точечную оценку фазового состояния, то нужен критерий для такого
выделения. Весьма часто за наилучшую оценку принимают
чебышевский центр информационного множества
мы
вынуждены считать эти множества наилучшими оценками неизвестного
состояния. Если же по какой-либо причине необходимо выделить
точечную оценку фазового состояния, то нужен критерий для такого
выделения. Весьма часто за наилучшую оценку принимают
чебышевский центр информационного множества ![]() [1,2,3].
[1,2,3].
![]() дают лишь
принципиальное решение задачи, которое в каждом конкретном
случае сопряжено со значительными трудностями при нахождении
нижних граней в (2.3) или пересечений множеств в
(2.6).
дают лишь
принципиальное решение задачи, которое в каждом конкретном
случае сопряжено со значительными трудностями при нахождении
нижних граней в (2.3) или пересечений множеств в
(2.6).