2. Симметрии и разделение задачи на независимые подзадачи.

2.1. Как известно, многие задачи математической физики могут быть сведены к некоторым вариационным равенствам или соответствующим им вариационным задачам на минимум подходящих квадратичных функционалов, порожденных соответствующими билинейными и линейными формами. Поэтому рассмотрим сначала абстрактную вариационную задачу. Покажем, что наличие некоторых инволюций (симметрий) в этой задаче позволяет свести ее к нескольким аналогичным независимым подзадачам меньшей размерности. Последнее обстоятельство имеет значение для увеличения точности аппроксимаций при практическом решении задач на малых и средних ЭВМ и на многопроцессорной вычислительной технике.

Пусть H -- вещественное линейное векторное пространство, -- алгебраически сопряженное к H пространство линейных функционалов на H, -- билинейная симметричная форма на , . Рассмотрим следующую вариационную задачу

Отметим некоторые свойства этой задачи. Если бы форма a была положительно определенной, то задача допускала бы не более одного решения. Существование решений в этой задаче обычно устанавливается с помощью привлечения тех или иных дополнительных топологических понятий и методов. Вопросы единственности и существования решений в случае конечномерного пространства H можно решить чисто алгебраическими средствами (сведением задачи к системе линейных алгебраических уравнений). Следующее свойство вытекает из билинейности формы a. Если v(f) -- некоторое решение задачи (2.1), соответствующее функционалу , v(g) -- некоторое решение этой же задачи, соответствующее функционалу , то для любых вещественных чисел и элемент будет решением задачи (2.1), соответствующим функционалу . Если бы для каждого задача (2.1) имела единственное решение , то оператор решения этой задачи был бы линейным на . В случае, когда форма a является неотрицательной, задача (2.1) эквивалентна задаче минимизации

если одна из задач допускает некоторое решение, то и другая допускает то же самое решение.

Пусть задан линейный инволютивный a-изометричный оператор , т.е.

Любой элемент однозначно раскладывается на S-четную и S-нечетную составляющие E(u) и O(u) соответственно :

Алгебраически сопряженный к S оператор инволютивен, поэтому любой элемент однозначно раскладывается на -четную и -нечетную составляющие и соответственно :

Отметим также следующие простые равенства

Таким образом, справедливы разложения в прямую сумму подпространств

Отметим, что для каждого элемента справедливы равенства

Теорема 2.1. Пусть v(f) -- некоторое решение задачи для . Тогда
1) Sv(f) есть решение задачи , соответствующее функционалу ;
2) E(v(f)) есть решение задачи , соответствующее функционалу , и есть решение задачи в подпространстве E(H) для функционала f или , т.е.



3) O(v(f)) есть решение задачи , соответствующее функционалу , и есть решение задачи в подпространстве O(H) для функционала f или , т.е.



4) если -- некоторое решение задачи в подпространстве E(H) для функционала f, -- некоторое решение задачи в подпространстве O(H) для функционала f, то -- решение задачи в H для функционала f;
5) если задача для каждого имеет единственное решение v(f), то дополнительно к предыдущим утверждениям выполняются равенства

Д о к а з а т е л ь с т в о. Первое утверждение теоремы следует из цепочки равенств

Второе утверждение вытекает из первого и цепочки равенств



Поскольку это равенство выполняется также и для любого элемента , причем и на E(H), то E(v(f)) является также решением задачи (2.1) в подпространстве E(H) для функционала f или . Третье утверждение теоремы доказывается аналогично второму. Докажем четвертое утверждение. Из определения решений и и свойств оператора S вытекают две цепочки равенств



справедливые для любого элемента , поэтому

т.е. является решением задачи (2.1) в H для функционала . Последнее утверждение следует из единственности решения задачи (2.1).

Теорема доказана.

Таким образом, наличие a-изометричной инволюции S на H позволяет свести решение задачи (2.1) или (2.2) к решению двух аналогичных независимых подзадач в подпространствах E(H) и O(H). Если функционал f является -четным или -нечетным, то решение одной из задач может оказаться тривиальным. С каждой из подзадач можно поступать как с исходной, т.е. попытаться найти соответствующие инволюции и разделить подзадачи на еще более ``мелкие'' и т.д. В частности, наличие на H попарно коммутирующих a-изометричных инволюций позволяет разделить исходную задачу на аналогичных независимых подзадач в соответствующих подпространствах пространства H. Некоторые из этих подзадач могут оказаться тривиальными, если функционал f обладает соответствующими четностями или нечетностями.

2.2. При решении задачи (2.1) или (2.2) приближенными методами (например, методом Галеркина или методом конечных элементов) часто приходится решать аналогичные задачи в каком-либо конечномерном подпространстве :

Эта задача эквивалентна системе линейных алгебраических уравнений

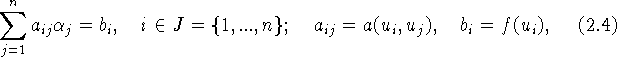
где -- какой-либо базис в V. Если -- решение задачи (2.3), то -- решение задачи (2.4), и наоборот. Детализируем схему предыдущего пункта для данного случая.

Пусть V и его базис являются S-инвариантными, т.е.

Легко заметить, что тогда перестановка на J является инволюцией (перестановкой порядка 2)

а матрица обладает следующей симметрией

Поскольку

то для S-четного (S-нечетного) элемента имеем

Понятно, что любой S-четный элемент из V (в частности, любое S-четное решение задачи (2.3), которое может соответствовать только -четному линейному функционалу) полностью определяется своими коэффициентами для индексов из произвольного подмножества , удовлетворяющего условиям:





Отметим, что в силу (2.7) для S-четного элемента из условий p(j) = j и s(j) = -1 следует . Последнее из условий для обеспечивает минимальность множества по числу элементов среди всех множеств, удовлетворяющих первым двум условиям.

Любой S-нечетный элемент из V (в частности, любое S-нечетное решение задачи (2.3), которое может соответствовать только -нечетному линейному функционалу) полностью определяется своими коэффициентами для индексов из произвольного подмножества , удовлетворяющего условиям :





Отметим, что в силу (2.7) для S-нечетного элемента из условий p(j) = j и s(j) = 1 следует . Последнее из условий для обеспечивает минимальность множества по числу элементов среди всех множеств, удовлетворяющих первым двум условиям. Легко проверить, что в качестве можно взять . Тогда и образуют разбиение J (их объединение равно J и пересечение пусто). Далее будем считать, что и образуют разбиение J.

Найдем базис в подпространстве . Разобъем множество индексов J на следующие части:



Из свойств следует, что попарные пересечения этих множеств пусты и , . Преобразуем разложение (по базису ) произвольного элемента

Последняя сумма равна нулю в силу (2.7). Преобразуем третью сумму, используя (2.7) и тот факт, что для

Таким образом,

где для , для . Из найденного представления, включения для , линейной независимости системы элементов следует, что эта система элементов образует базис в E(V).

Аналогичным способом можно показать, что система элементов , где для , для , , , , образуют базис в подпространстве . При этом для любого элемента справедливы представления

Пусть , v -- решение задачи (2.3). Составим системы уравнений для нахождения S-четной E(v) и S-нечетной O(v) компонент решения v. Компонента , в силу теоремы 2.1, является решением задачи (2.3) на подпространстве E(V) для функционала ( на E(V)). Эта задача равносильна нахождению коэффициентов , из системы линейных алгебраических уравнений

Выразим элементы системы (2.8) через элементы системы (2.4) :

Компонента , в силу теоремы 2.1, является решением задачи (2.3) на подпространстве O(V) для функционала (). Эта задача равносильна нахождению коэффициентов , из системы линейных уравнений

Выразим элементы системы (2.9) через элементы системы (2.4) :

Допустим, что системы (2.8), (2.9) решены. Выпишем формулы ``сборки'' решения по коэффициентам и :











следовательно,



Используя представления E(v) = (v + Sv)/2 и O(v) = (v - Sv)/2, легко получить формулы ``разборки'' решения :

Полученные в этом пункте результаты сформулируем в виде утверждения.

Теорема 2.2. Пусть на множестве индексов J заданы перестановка порядка 2 и функция , удовлетворяющие условию , пусть матрица системы линейных уравнений удовлетворяет условию симметрии . Тогда решение системы уравнений сводится к решению двух независимых линейных систем уравнений и меньших размерностей. Из любых решений систем и можно получить решение системы по формулам ``сборки'' . Из любого решения системы можно получить решения систем и по формулам ``разборки'' .

Если функционал f является -четным или -нечетным, то одна из систем (2.8), (2.9) становится однородной и имеет по крайней мере нулевое решение. Каждую из систем (2.8), (2.9) можно пытаться аналогичным способом разбить на новые подзадачи и т.д. В частности, наличие на J попарно коммутирующих перестановок и сопутствующих им функций , удовлетворяющих условиям (2.5), (2.6) и условию

позволяет разбить систему (2.4) на независимых подсистем меньших размерностей. ``Разборку'' и ``сборку'' решений можно осуществлять последовательно в соответствии с теоремой 2.2. Подобный подход может быть положен в основу распараллеливания алгоритмов решения вариационных задач или систем алгебраических уравнений.

Отметим, что другие способы упрощения решения систем линейных уравнений, преимущественно с теплицевыми матрицами, рассматривались, например, в [26].