1. Описание модели и ее численная реализация.

Рассмотрим постановку задачи и ее преобразование к более удобной форме, опишем схему расчетов и некоторые ее детали. Приведем результаты расчетов модельного примера, который отражает в себе основные черты реального процесса.

1.1. Постановка задачи. Ниже используются следующие обозначения: ; ; означает, что перечисляются все тройки индексов , полученные из круговой перестановкой; мы предполагаем суммирование по повторяющимся индексам, если не оговорено противное; в параграфе 2 знак суммирования все же сохраняется, поскольку там необходимо знать, по какой совокупности индексов оно происходит. В области рассматривается медленное движение вязкой неоднородной несжимаемой жидкости в поле силы тяжести. Предпологается, что физические параметры жидкости являются переменными и задаются в начальный момент времени. В процессе движения жидкости значения ее плотности и вязкости переносятся вместе со средой. Это движение в декартовых координатах описывается известными квазистационарными уравнениями Навье -- Стокса [13, 14, 15, 16, 17, 18, 19, 20]

где -- вектор скорости, -- вектор внешних массовых сил, g -- ускорение свободного падения, p -- давление, -- плотность, -- динамическая вязкость, -- тензор скоростей деформаций.

Уравнение несжимаемости (неразрывности) задается в форме

перенос плотности и вязкости описывается уравнениями



На границе области рассмoтрим граничные условия прилипания

или непротекания вместе с идеальным скольжением

-- единичная внешняя нормаль в точках границы .

Таким образом, задача состоит в расчете функций

удовлетворяющих в области при уравнениям (1.1)- (1.4), граничным условиям (1.5) или (1.6) и начальным условиям из (1.3) , (1.4). Отметим, что эта задача имеет не более одного решения.

1.2. Преобразование задачи. Исключим из рассмотрения давление p и условие несжимаемости (1.2), введя векторный потенциал по формуле . Выполним операцию над равенством (1.1), тогда, учитывая тождества и , получим систему уравнений для нахождения функций , , , которая в развернутой форме имеет вид :











граничные условия для в случае прилипания имеют вид



граничные условия для в случае непротекания и идеального скольжения можно взять в виде (без суммирования по повторяющимся индексам)

Компоненты тензора в развернутой форме имеют вид (без суммирования по повторяющимся индексам)

Равенства (1.7), (1.8), (1.9) умножим соответственно на компоненты , , пробной вектор-функции , удовлетворяющей граничным условиям (1.13) или (1.14). Результаты умножения проинтегрируем по и перебросим с помощью формулы интегрирования по частям вторые производные на пробные функции. После сложения получившихся трех равенств будем иметь вариационное равенство, которое должно выполняться для любой пробной вектор-функции , принадлежащей тому же классу гладкости и тем же граничным условиям, что и функция :

где



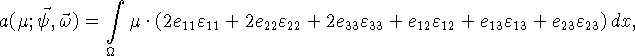
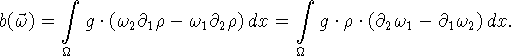
Величины и выражаются через по формулам (1.15); величины и выражаются через по тем же формулам, где вместо нужно подставить , . Отметим, что билинейная форма симметрична, то-есть , и неотрицательна: для любой допустимой ; правая часть преобразуется к виду, в котором отсутствует дифференцирование функции .

Итак, решение исходной задачи сведено к нахождению функций , , , удовлетворяющих в области при вариационному уравнению (1.16), начальным условиям из (1.10), (1.11) и граничным условиям (1.13) или (1.14).

Преобразованная задача (1.16) имеет бесконечно много решений. Действительно, если -- некоторое решение этой задачи, то , где -- произвольная функция из , также будет решением преобразованной задачи. Тем не менее, можно показать, что граничные условия (1.13) или (1.14) обеспечивают, единственность нахождения рассматриваемых ниже дискретных аппроксимаций. В задаче (1.16) никакие граничные условия не могут обеспечить единственность ее решения. Для определенности можно рассматривать нормальные решения, т.е. решения минимизирующие какую-либо норму.

1.3. Схема расчета задачи. Начальные данные и из (1.10), (1.11) подставляются в краевую задачу (1.7) - (1.9) с граничными условиями (1.13) или (1.14) для расчета векторного потенциала и поля скоростей в момент времени , затем эти поля используются в задачах (1.10), (1.11) для расчета вязкости и плотности в области в момент времени . Далее момент времени принимается за начальный и схема расчетов повторяется. Поле векторного потенциала рассчитывается методом Галеркина с базисом, состоящим из трикубических сплайнов на соответствующих кубических элементах (этот базис строится ниже). Вязкость и плотность могут вычисляться из уравнений переноса каким-либо методом, например, сдвигом вдоль поля скоростей и последующей интерполяции на всю область. Шаг по времени может выбираться автоматически так, чтобы максимальное смещение материальных точек среды не превосходило заданной достаточно малой величины h. Для этого отыскивается на соответствующих элементах, а затем полагается .

Заметим, если функции и симметричны относительно плоскостей и , то поле скоростей , вязкость и плотность будут оставаться симметричными относительно этих плоскостей и во все моменты времени . Поэтому, согласно результатам параграфов 2 и 3, решение задачи достаточно найти в области

и затем результат симметрично отразить относительно упомянутых плоскостей. На самих плоскостях следует рассматривать граничные условия непротекания и идеального скольжения. Если функция симметрична относительно плоскостей и , то, согласно результатам параграфов 2 и 3, решение исходной задачи можно свести к решению четырех независимых подзадач в . Если , то решение исходной задачи можно свести к решению восьми независимых подзадач в

Возможны и другие варианты использования симметрий, см. параграфы 2 и 3.

1.4. Детали вычислительной схемы. Опишем кратко способ построения базисных элементов, который опирается на понятие одномерного базисного кубического сплайна. Одномерным кубическим сплайном s(x), соответствующим какому-либо разбиению отрезка , называется [23] функция, удовлетворяющая следующим двум условиям (краевые условия пока не указываем):
1) на каждом отрезке разбиения она является кубическим полиномом;
2) функции s(x), , непрерывны на области определения.
При решении задачи интерполяции требуется найти сплайн, который в узлах разбиения совпадает со значениями интерполируемой функции. Кроме того, для однозначного представления интерполируемой функции необходимо наложить два дополнительных граничных условия. Таким образом, для однозначного представления кубическим сплайном на концах отрезка должны выполняться по два граничных условия, например:

или

Введем на отрезке разбиение

Точкам разбиения , поставим в соответствие сплайны , которые имеют вид

(носитель=



(носители=



(носитель=

Носитель сплайна имеет длину 4h, у остальных сплайнов длина носителя 3h. Ниже в таблицах указаны коэффициенты кубических полиномов, составляющих сплайн, при соответствующих степенях аргумента; под каждой таблицей перечисляются граничные условия, которым удовлетворяют соответствующие сплайны:

:

\

в качестве или выбирается один из следующих трех сплайнов или их некоторая комбинация

:



:



:



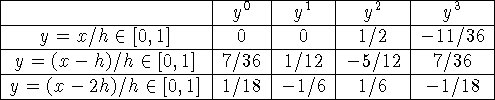
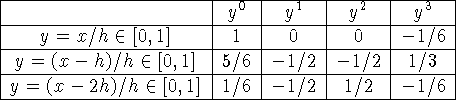
в качестве или выбирается один из следующих трех сплайнов или их некоторая комбинация
:





:

\



:





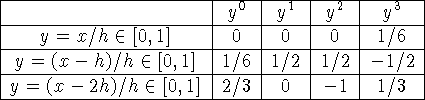
Конкретный вид сплайнов , , , будет зависеть от типа граничных условий для интерполируемой функции. При рассмотрении условий идеального скольжения сплайны , не принимаются во внимание. Набор сплайнов , , линейно независим, проэтому является базисом в натянутом на него линейном пространстве. Подробная теория сплайнов с анализом их сходимости дается, например, в [23]. Отметим одно важное свойство системы стандартных и базисных сплайнов: набор стандартных сплайнов симметричен относительно середины отрезка, на котором они рассматриваются; при симметричных граничных условиях для интерполируемой функции систему базисных сплайнов , , можно выбрать симметричной относительно середины отрезка [0,l].

В области рассмотрим прямоугольную сетку с узлами в точках (узел сетки имеет координаты )

Рассмотрим пространство, базисом в котором является множество функций, являющихся всевозможными произведениями трех одномерных базисных сплайнов относительно соответствующих переменных (далее такие элементы иногда будем называть трикубическими сплайнами или базисными функциями)

Сплайны зависят, вообще говоря, от номера оси, т.к. на каждой из осей могут рассматриваться свои разбиения отрезка. С целью упрощения обозначений эту зависимость опускаем.

Приближения к искомым функциям будем искать из указанного выше пространства. Поскольку, в зависимости от вида граничных условий, компоненты векторного потенциала будут приближаться, вообще говоря, разными наборами базисных функций, то для отличия одного набора базисных функций от другого будем использовать верхний индекс. Базисные функции для приближения и будем отличать соответствующими надчеркиваниями. Отметим одно важное свойство набора базисных функций, о котором в одномерном случае упоминалось выше: если краевые условия задачи симметричны относительно плоскости , то таковыми можно задать и наборы базисных функций.

Искомую функцию будем приближать линейными комбинациями базисных вектор-функций ,

здесь - орт соответствующей координатной оси.

Функции и будем приближать линейными комбинациями по системам базисных функций, которые строятся аналогично предыдущей (при этом в качестве базисных функций достаточно использовать кусочно-линейные функции)

Выпишем систему линейных алгебраических уравнений для нахождения приближения к функции , то есть неизвестных коэффициентов в (1.19). Для этого подставим (1.19)-(1.21) в вариационное уравнение (1.16) и по очереди переберем все пробные функции :

После перегруппировки членов приходим к следующей системе линейных алгебраических уравнений:





где коэффициенты имеют следующий вид:

Коэфициенты A, B и C с индексами являются интегралами от произведений базисных сплайнов и их производных:





где -- производная порядка . Коэффициенты в правых частях уравнений принимают вид





Интегралы A, B, C, P, Q, R (с соответствующими индексами) могут быть вычислены аналитически и рассчитываются заранее. Уравнения линейной системы формируются независимо друг от друга, поэтому процесс формирования матрицы системы и вектора правой части может быть распараллелен.

Введем следующую линейную нумерацию уравнений и неизвестных: объекту с индексом (p,i,j,k), где , , , , припишем номер

При такой нумерации базисных функций и неизвестных коэффициентов матрица системы будет ленточной с шириной ленты пропорциональной и практически не зависящей от . При этой нумерации матрица системы получается симметричной и положительно определенной.

Полученную линейную систему можно решать точными и приближенными методами. Существенная трудность решения системы на ЭВМ состоит в ее очень большой размерности. Так для сетки получается 9000000 элементов матрицы и 3000 неизвестных. Отметим, что среди элементов матрицы будет много нулевых; этот факт можно учитывать при хранении матрицы и решении системы уравнений. В качестве базового метода решения системы уравнений выбран метод Холесского (метод квадратного корня) [21, 22]. Как указывалось выше, для задачи с симметричными граничными условиями система базисных функций может быть выбрана симметричной, что влечет наличие некоторых - симметричных инволюций на пространстве приближенных решений. Тогда, согласно результатам параграфов 2 и 3, решение системы линейных уравнений можно свести к решению нескольких независимых подсистем. Симметрию матрицы системы можно использовать также для сокращения вычислений элементов матрицы и уменьшения объемa памяти, необходимой для их хранения. Но главный выигрыш получается благодаря тому, что, если, например, решение системы с примерно неизвестными сводится к решению 8 независимых подсистем примерно с неизвестными каждая, то матрицы и соответствующие фактор-матрицы этих подсистем, с учетом ленточной структуры, содержат примерно в 32 раза меньше ненулевых элементов каждая, чем матрица и соответствующая факторматрица исходный системы. Все вместе они содержат в 4 раза меньше ненулевых элементов.

Обратимся к процедурам нахождение вязкости и плотности. Подставим в (1.10), (1.11) представление искомых функций в виде сплайн-интерполянтов. Умножим обе части этого равенства на пробные функции

проинтегрируем обе части по области и получим систему линейных дифференциальных уравнений для нахождения неизвестных





где

Для нахождения вязкости соответствующая система линейных дифференциальных уравнений находится аналогично. Системы могут решаться любым методом прогноза и коррекции (например, методом Рунге - Кутта).

Возможны другие варианты расчета плотности и вязкости, основанные на методе обратного хода и позволяющие избежать образования при расчете так называемых ложных диапировых структур [24, 25]. Например, можно поступить следующим образом. Уравнения (1.3), (1.4) имеют характеристики, описываемые системой обыкновенных дифференциальных уравнений

где x(t) нужно рассматривать как вектор с компонентами . Вдоль характеристик плотность и вязкость сохраняют свои значения

Методом Эйлера расчет характеристик в обратном времени с шагом можно вести по формуле

Отсюда получаем

Таким образом, полученные формулы позволяют определять плотность и вязкость в момент времени t по известным распределениям плотности и вязкости на предыдущем шаге по времени и по известному полю скоростей, уже рассчитанному в момент времени t.

1.5. Вычисление прогиба поверхности. Погружение (прогиб) поверхности в каждый момент времени будем вычислять по формуле [11, 25]:

компонента рассчитывается по формуле

где давление p с точностью до константы можно определить с помощью интегрирования:

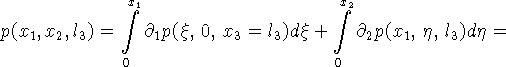
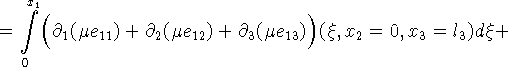
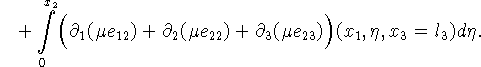
Легко заметить, что поверхность

отличается от реальной сдвигом на константу вдоль оси (профили этих поверхностей одинаковы). Реальная поверхность должна быть такова, чтобы выполнялся закон сохранения массы, и поэтому реальную поверхность можно рассчитать по формуле

где A - среднее значение , например,

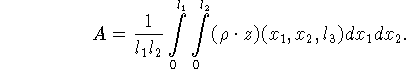
1.6. Тестирование решения задачи. Точность решения всей задачи определяется главным образом той точностью, с которой удается решить систему уравнений Стокса с помощью предложенной вычислительной схемы. Проще всего получить представление о величине погрешности используемой аппроксимации -- это решить приближенным методом задачу, для которой известно точное решение, и сравнить приближенное решение с точным. Это просто сделать, если ``идти в обратном направлении'': надо взять гладкую вектор-функцию, удовлетворяющую краевым условиям, объявить ее решением, подставить в оператор системы уравнений и получить требуемую правую часть.

Зададим функцию следующим образом:

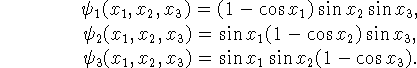
На границе области функция удовлетворяют условиям идеального скольжения с непроницаемостью.

Подставляя в формулу (1.16), получаем правую часть для тестового примера:





причем эти интегралы можно вычислить точно.

Тестовый пример аппроксимировался на сетке из узлов при постоянной вязкости. В этом случае задача обладает тремя пространственными симметриями относительно плоскостей , поэтому решение системы сводится к решению 8 независимых подсистем , размерность вектора неизвестных в которых в 8 раз меньше размерности вектора неизвестных для исходной системы. Полученное приближенное решение , , удовлетворяет точности

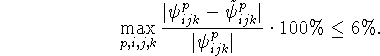
Другой способ оценки точности решения основан на законе сохранения массы. Общая масса жидкости в области должна оставаться постоянной во времени. Ее легко вычислить с помощью интегрирования плотности по области . Было установлено, что изменение массы не превышает 0.3% на каждом шаге по времени.

1.7. Расчеты. Численно моделировалось погружение тонкой эклогитовой линзы в поле силы тяжести в среде с постоянной вязкостью. Вычисления проводились при следующих значениях безразмерных параметров задачи.

Область представляла собой параллелепипед

Линза представляла собой часть эллиптического цилиндра

Вязкость , функция задавалась формулой

Аппроксимация исходной задачи производилась на сетке из узлов. Векторный потенциал аппроксимировался трикубическими сплайнами. В качестве граничных условий взяты условия идеального скольжения. Система линейных алгебраических уравнений решалась методом Холесского. Плотность аппроксимировалась на сетке из узлов с помощью трилинейных функций. Использование трилинейных функций позволило аппроксимировать разрывную функцию плотности лучше, чем при интерполяции трикубическими сплайнами. Шаг по времени, с которым проводились пересчеты плотности, выбирался по следующей формуле:

Вычисления проводились на IBM PC-486/66/8. Восемь фактор-матриц в методе Холесского формировалась 2.5 часа, один шаг по времени делался за 0.3 часа (сюда входило: решение системы линейных алгебраических уравнений с помощью фактор-матриц, расчет поля скоростей по векторному потенциалу на сетке , нахождение плотности на сетке ). Тот же самый пример был расчитан на многопроцессорном комплексе МВС-100. Расчет проводился на 8 процессорах, факторматрицы формировались за 19 минут, один шаг по времени делался за 4 минуты.

Результаты численных расчетов приводятся в виде плоских сечений ( и ) в различные моменты времени (t=0, t=64, t=96). Поля скоростей обозначаются стрелками (длина стрелки прямо пропорциональна величине скорости), включения более плотного тела обозначаются штриховкой. На последних рисунках изображены прогиб поверхности, линии и множества уровня. Масштаб по времени равен 0.5 млн. лет. По расчетам в средних сечениях средняя скорость погружения линзы на рассматриваемом промежутке времени примерно равна 0.92 км/млн.лет; поверхность опускается вслед за линзой примерно 10 млн. лет на глубину 2.8 км, а затем начинает медленно подниматся со средней скоростью примерно 9.73 м/млн.лет.