| Использование раз. способов и эффектов |
Кол. GIF-обр. |
Размер GIF-обр.(байт) |
| Все выр. - образ с "antialias"+"scalable fonts" |
6 |
10.335 |
| Все выр. - образ с "antialias" |
6 |
7.085 |
| Все выр. - образ с "noantialias" |
6 |
4.995 |
| Способ "Простая математика" с "antialias"+"scalable fonts"+"reuse=2" |
9 |
1.849 |
| Способ "Простая математика" с "antialias"+"reuse=2" |
9 |
1.394 |
| Способ "Простая математика" с "noantialias"+"reuse=2" |
9 |
1.022 |
| Способ "Простая математика" с "antialias"+"reuse=0" |
37 |
5.425 |
| Способ "Простая математика" с "noantialias"+"reuse=0" |
37 |
3.908 |
| Конвертор TTH |
0 |
0 |
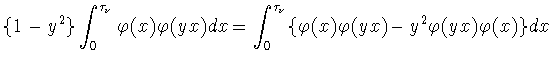
![$\displaystyle \int_0^{\tau_\nu}\Biggl[-\{\varphi''(x)-q(x)\varphi(x)\}\varphi(yx)+
\{\varphi''(yx)-q(x)\varphi(yx)\}\varphi(x)\Biggr]dx=$](NIimg4.gif)
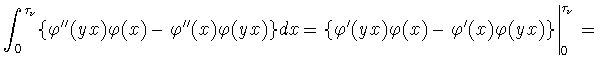
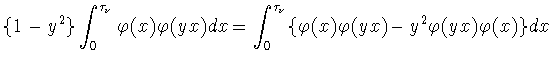
![$\displaystyle \int_0^{\tau_\nu}\Biggl[-\{\varphi''(x)-q(x)\varphi(x)\}\varphi(yx)+
\{\varphi''(yx)-q(x)\varphi(yx)\}\varphi(x)\Biggr]dx=$](NIimg4.gif)
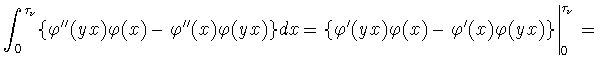
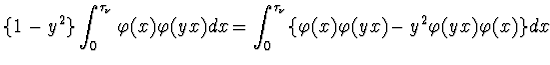
![$\displaystyle \int_0^{\tau_\nu}\Biggl[-\{\varphi''(x)-q(x)\varphi(x)\}\varphi(yx)+
\{\varphi''(yx)-q(x)\varphi(yx)\}\varphi(x)\Biggr]dx=$](Pimg4.gif)
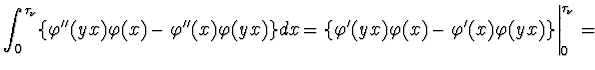
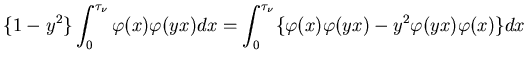
![$\displaystyle \int_0^{\tau_\nu}\Biggl[-\{\varphi''(x)-q(x)\varphi(x)\}\varphi(yx)+
\{\varphi''(yx)-q(x)\varphi(yx)\}\varphi(x)\Biggr]dx=$](SAIimg4.gif)