

Next: VI Задачи дизъюктивного программирования
Up: book
Previous: IV Двойственность для несобственных
Объектом рассмотрения будет задача
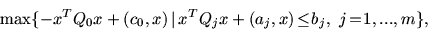 |
(1) |
в которой
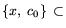 Rn,
{ Qk }k=0m
-- матрицы размерности n x n. Сквозным образом будем
предполагать матрицу Q0 положительно определенной (т.е.
Rn,
{ Qk }k=0m
-- матрицы размерности n x n. Сквозным образом будем
предполагать матрицу Q0 положительно определенной (т.е.
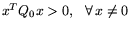 ), матрицы
{ Qj }j=1m --
неотрицательно определенными (т.е.
), матрицы
{ Qj }j=1m --
неотрицательно определенными (т.е.
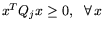 ).
Если все Qj,
).
Если все Qj, 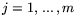 , -- нулевые матрицы, то (1) --
общая задача квадратичного программирования:
, -- нулевые матрицы, то (1) --
общая задача квадратичного программирования:
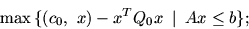 |
(2) |
здесь A -- матрица со строками aj, b -- вектор с
координатами bj, 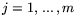 . Если в (2) вместо Q0
взять
. Если в (2) вместо Q0
взять
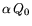 ,
,
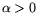 , то получим задачу
, то получим задачу
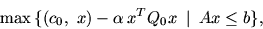 |
(3) |
выступающую в качестве регуляризирующей (по Тихонову) задачу
линейного программирования
Ниже будут рассмотрены некоторые вопросы, относящиеся к теории
задач вида (1), в первую очередь, вопросы двойственности,
регуляризации, несобственности.
1. Двойственность
Если
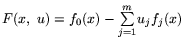 --
функция Лагранжа, поставленная в соответствие задаче математического
программирования
--
функция Лагранжа, поставленная в соответствие задаче математического
программирования
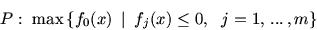 |
(4) |
с дифференцируемыми функциями
{fk(x)}k=0m, то
двойственной к P [1, § 23] является
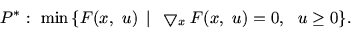 |
(5) |
Формирование такой двойственности основано на универсальной
схеме, в силу которой в качестве двойственной к P выступает задача
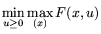 , что в случае
дифференцируемости функций fk(x),
, что в случае
дифференцируемости функций fk(x),
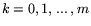 приводит к
выписанной задаче P*.
приводит к
выписанной задаче P*.
Если (4) -- задача выпуклого программирования (ВП), то
справедливо
Утверждение 1 (прямая теорема двойственности)
[1, теорема 24.3].
Пусть задача выпуклого программирования P удовлетворяет условиям:
- 10.
- P разрешима.
- 20.
- Функции
{fk(x)}k=0m дифференцируемы.
- 30.
- Существует допустимый для P вектор p такой, что
fj(p)<0 для нелинейных fj(x) (условие регулярности).
Тогда P* разрешима, при этом
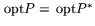 .
.
Далее функции
{fk(x)}k=0m будут иметь вид,
соответствующий задаче (1), т.е.
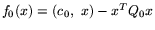 ,
,
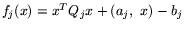 ,
, 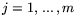 .
.
Лемма 1
Задача
P*, определенная согласно (
5) для
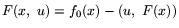
,
![$F(x) = [f_1(x),\,...\,,f_m(x)]$](img1128.gif)
, может быть
эквивалентно преобразована к виду
где
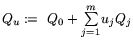
.
Д о к а з а т е л ь с т в о. Элементарные преобразования функции Лагранжа
![$F(x,\ u) =
(c_0,\ x) -x^T Q_0 x -\mbox{$\sum\limits_{j=1}^{m}$} u_j [x^T Q_j x +(a_j,\ x) -b_j]$](img1131.gif) дают
дают
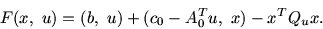 |
(6) |
Так как
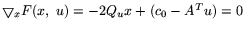
, то
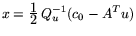
. Подставляя найденное
значение для
x в соотношение (
6), получаем тот вид
минимизируемой функции, который и фигурирует в двойственной
задаче (1)
*.
З а м е ч а н и е 1. Если в исходной задаче (1)
имеется требование 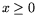 , то (1)* принимает вид
, то (1)* принимает вид
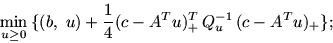 |
(7) |
здесь
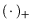
означает положительную срезку
вектора, стоящего внутри скобки.
З а м е ч а н и е 2. Если положить
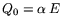 ,
,
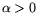 (E -- единичная матрица), Qj=0,
(E -- единичная матрица), Qj=0, 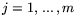 , то
задача (1) примет вид
, то
задача (1) примет вид
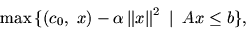 |
(8) |
а задача (1)
* -- вид
На самом деле, как в случае задач (8) и (8)*, так и в
более общей ситуации задач (1) и (1)*, справедлив и
обратный переход, связанный с формированием двойственных задач,
т.е. ((1)*)* и ((8)*)*. Здесь справедлива взаимная
двойственность, т.е.
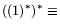 (1) и, в частности,
(1) и, в частности,
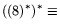 (8). Во избежание громоздких преобразований
ограничимся проверкой второго соотношения.
(8). Во избежание громоздких преобразований
ограничимся проверкой второго соотношения.
Лемма 2
Задача ((8)
*)
*, двойственная к (8)
*, совпадает с задачей (
8).
Д о к а з а т е л ь с т в о. Перепишем задачу (8)* в виде
и поставим ей в соответствие функцию Лагранжа
в которой
u и
y -- свободные переменные, а
x и
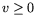
-- множители Лагранжа, соотнесенные ограничениям
y =
c0-
ATu и
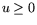
соответственно. Задача ((8)
*)
*,
двойственная к (8)
*, запишется в виде
Нужно показать, что она может быть преобразована в
задачу (
8).
Сделаем преобразования функции 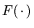 и уравнения
и уравнения
![$\bigtriangledown _{[u,y]} F(\,\cdot\,) =0$](img1147.gif) :
:
С учетом этих соотношений получаем
а сама задача ((8)
*)
* примет вид
т.е. вид задачи (
8). Лемма доказана.
Теорема 1 (двойственности)
Пусть в задаче (
1)
Q0 -- положительно определенная
матрица,
{Q
j}
j=1k -- неотрицательно определенные. Если
для ограничений задачи (
1) выполнено условие регулярности
(пусть в форме 3
0), то задачи (
1) и (1)
*
разрешимы, при этом
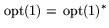
.
Д е й с т в и т е л ь н о, из совместности
системы ограничений задачи (1) и ограниченности лебеговых
множеств
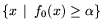 , где
f0(x) = (c0,
x) -xT Q0 x, вытекает разрешимость этой задачи. В силу общей
теоремы двойственности, сформулированной выше как
утверждение 1, разрешима и задача (5), соотнесенная
к (1), причем opt(1)=opt(5). Но так как
переход от задачи (5) к задаче (1)* был эквивалентным (хотя
и сопровождавшимся исключением из записи задачи переменной x), то
равенство opt(1)=opt(1)* соблюдается.
, где
f0(x) = (c0,
x) -xT Q0 x, вытекает разрешимость этой задачи. В силу общей
теоремы двойственности, сформулированной выше как
утверждение 1, разрешима и задача (5), соотнесенная
к (1), причем opt(1)=opt(5). Но так как
переход от задачи (5) к задаче (1)* был эквивалентным (хотя
и сопровождавшимся исключением из записи задачи переменной x), то
равенство opt(1)=opt(1)* соблюдается.
З а м е ч а н и е 3. Применительно к частной
ситуации (8)-(8)* сформулированной теореме можно
придать такую редакцию:
Если
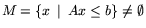 , то задачи
(8) и (8)* разрешимы, при этом opt(8)=opt(8)*.
, то задачи
(8) и (8)* разрешимы, при этом opt(8)=opt(8)*.
З а м е ч а н и е 4. Если в (8) есть
требование 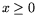 , то (8)* принимает вид
, то (8)* принимает вид
2. Взаимная сопряженность методов
регуляризации и квадратичных штрафных
функций для задач линейного
программирования
В этом пункте свяжем с задачей линейного программирования
(ЛП) вида
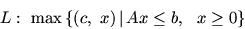 |
(9) |
задачу регуляризации (по Тихонову)
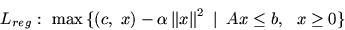 |
(10) |
и задачу, реализующую квадратичный метод штрафных функций,
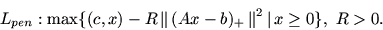 |
(11) |
Приведем хорошо известные факты (см., например, [3]):
Если v0 -- двойственная оценка неравенства
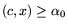 (:=optL) в задаче
(:=optL) в задаче
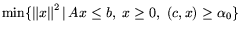 , то при
, то при
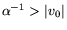 :
:
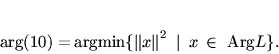 |
(12) |
Если L разрешима и
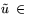 ArgL*, то
ArgL*, то
 |
(13) |
Запишем задачу, двойственную к (10), имея в виду схему
перехода от (1) к (1)*:
С другой стороны, запишем задачу, двойственная к которой
совпадала бы с Lpen. Такой задачей будет
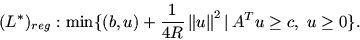 |
(14) |
Задача (10)*, полученная по схеме перехода (1)
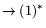 , как раз и дает задачу (11), что легко проверяется.
Обсуждаемые задачи свяжем схемой:
, как раз и дает задачу (11), что легко проверяется.
Обсуждаемые задачи свяжем схемой:
Приведенная схема фиксирует следующие факты:
- 1)
- Двойственная задача (10)* к задаче регуляризации Lreg
реализует квадратичный метод штрафных функций для L* --
двойственной к L (и обратно).
- 2)
- Двойственная к задаче (L*)reg, т.е. к задаче,
регуляризирующей L*, реализует квадратичный метод
штрафных функций для L (и обратно).
Приведенные факты как раз и выражают смысл того, что метод
регуляризации и квадратичный метод штрафных функций находятся в
соотношении взаимной сопряженности. Это обстоятельство было
вскрыто в работе автора [2] (см. формулы (8) и (9) этой
работы). С учетом соотношения (12) (также принадлежащего
автору) отсюда следует утверждение, смысл которого в следующем:
хотя квадратичный метод штрафных функций решает задачу L
приближенно, тем не менее двойственная к нему задача решает
задачу L* точно. Строгой формулировкой этого результата автор в
то время не располагал (о нем мне сообщил в 1995 г. А.И.Голиков).
Теперь приведем строгую формулировку этого факта, положив в
основу задачу
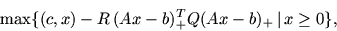 |
(15) |
соотнесенную задаче L в соответствии с квадратичным методом
штрафных функций; здесь R>0 -- штрафной параметр, Q --
положительно определенная матрица. В соответствии со схемой
двойственности (1)
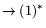 задача (15) будет
двойственной к
задача (15) будет
двойственной к
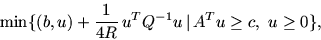 |
(16) |
т.е.
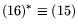 . Последняя выступает как задача
регуляризации (по Тихонову) задачи L* при стабилизаторе uT
Q-1 u. Теорема 1 в рассматриваемой ситуации принимает
следующую простую формулировку.
. Последняя выступает как задача
регуляризации (по Тихонову) задачи L* при стабилизаторе uT
Q-1 u. Теорема 1 в рассматриваемой ситуации принимает
следующую простую формулировку.
Утверждение 2
Если
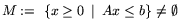
, то задачи
(
15) и (
16) разрешимы, при этом
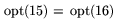
.
З а м е ч а н и е 5. В нашем случае соотношения
(12) и (13) принимают вид:
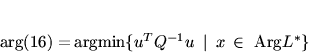 |
(17) |
при
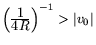
(т.е. при
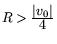
), где
v0 --
двойственная оценка неравенства
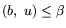
в задаче
где
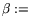
opt
L*.
Если задача L разрешима и
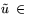 ArgL*, то
ArgL*, то
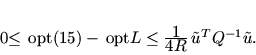 |
(18) |
Теорема 2
Если в квадратичном методе штрафных функций (
15)
параметр
R выбран в соответствии с замечанием 5, т.е.
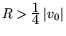
, то
где
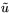
--
нормальное решение
(в смысле
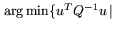
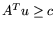
,
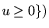
задачи
L*.
Д е й с т в и т е л ь н о, с одной стороны,
согласно (17):
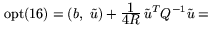 opt
opt
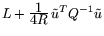 ; с
; с
другой -- в соответствии с
утверждением 2: opt(15)=opt(16), т.е.
что и требовалось.
3. Несобственные задачи квадратичного
программирования
Метод тихоновской регуляризации и метод квадратичных
штрафных функций допускают соединение в рамках одной задачи,
соотнесенной задаче L, пусть в постановке (9). Построим задачи
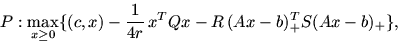 |
(19) |
![\begin{displaymath}
\begin{array}{c}
P^*: \min \{(b, u)
+\frac{\textstyle 1}{\t...
... +\\ [12pt]
+ r\,(c-A^Tu)_+^T Q^{-1} (c-A^Tu)_+ \};
\end{array}\end{displaymath}](img1189.gif) |
(20) |
здесь Q и S -- положительно определенные матрицы,
R и r -- положительные параметры. Задачи P и P*
являются взаимно двойственными в смысле того правила формирования
двойственности, которое было реализовано в ч. 1, в
частности, формирование задачи (1)* из (1) и (16)
из (15). Конечно, сказанное требует обоснования, хотя и носит
чисто выкладочный характер. В силу определенной громоздкости этих
выкладок обоснование опускаем.
Для анализа связей между задачами P и L, а также P*
и L*, выпишем отдельно задачи
| |
|
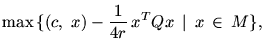 |
(21) |
| |
|
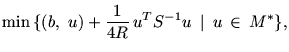 |
(22) |
где
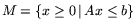 ,
,
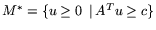 .
Двойственными к ним будут
.
Двойственными к ним будут
Переход от задач (21) и (22) к P и P* связан
с применением к первым техники квадратичного метода штрафных функций,
для которого имеют место оценки уклонения. А именно, если,
например, речь идет о задаче
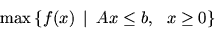 |
(23) |
и ее редукции к задаче
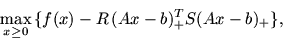 |
(24) |
то в ситуации разрешимости задачи (23) справедлива оценка
где
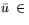 Arg(23)* [см., например, [3],
теорема 5.2]. Применительно к ситуации задачи (21) эта оценка
запишется так:
Arg(23)* [см., например, [3],
теорема 5.2]. Применительно к ситуации задачи (21) эта оценка
запишется так:
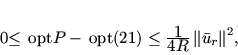 |
(25) |
где
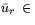 Arg(21)*. В соответствии
с (17) при достаточно большом r>0:
Arg(21)*. В соответствии
с (17) при достаточно большом r>0:
следовательно,
Используя это соотношение, получаем
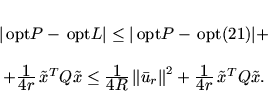 |
(26) |
Аналогично:
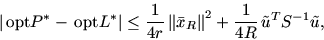 |
(27) |
где
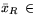 Arg(22)*,
Arg(22)*,
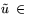 Arg
Arg
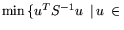 ArgL*}.
Подведем итоги (в форме теоремы) по совокупности свойств,
связывающих задачи (19) и (20).
ArgL*}.
Подведем итоги (в форме теоремы) по совокупности свойств,
связывающих задачи (19) и (20).
Теорема 3
Задачи
P и
P* (т.е. (
19) и (
20)) связывают
следующие утверждения:
- 10.
- P и P* взаимно двойственны, в частности,
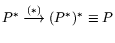 .
.
- 20.
- P и P* разрешимы независимо от разрешимости или
неразрешимости L.
- 30.
-
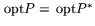 .
.
- 40.
- Если E -- общее значение левых частей в соотношениях
(26) и (27), то
(смысл 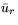 и
и 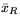 разъяснен выше).
разъяснен выше).
Сделаем пояснения к каждому пункту сформулированной выше теоремы.
- Чтобы получить вид задачи P* как двойственной к P, вначале
P следует переписать в виде
далее, построить для нее функцию Лагранжа
F(x,y;u,v,w) =
через которую и строится двойственная задача в форме:
Последняя же путем эквивалентных преобразований приводится к
виду P*. По аналогичной схеме проверяется и обратный переход,
а именно:
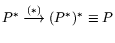 .
.
- Разрешимость задач P и P* будет следовать из проверки
хотя бы того факта, что каждое из лебеговых множеств
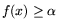 ,
,
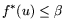 выпукло и ограничено (может быть и
пустым); здесь f(x) -- максимизируемая функция в
задаче P, f*(u) -- минимизируемая функция в задаче P*,
выпукло и ограничено (может быть и
пустым); здесь f(x) -- максимизируемая функция в
задаче P, f*(u) -- минимизируемая функция в задаче P*,
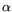 и
и
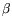 -- действительные числа.
-- действительные числа.
- Свойство 30 вытекает из утверждения 1.
- Оценка для E составляет содержание неравенств (26) и
(27).
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ
- Еремин И.И., Астафьев Н.Н. Введение в теорию линейного
и выпуклого программирования. -M.: Наука, 1976.
-190 с.
- Еремин И.И. Несобственные задачи квадратичного
программирования и вопросы регуляризации // Сб. `Параметрическая
оптимизация и методы аппроксимации несобственных задач
математического программирования''. -Свердловск: УНЦ АН СССР,
1985. -C. 47-53.
- Еремин И.И. Противоречивые модели оптимального
планирования.
-M.: Наука, 1988. -160 с.


Next: VI Задачи дизъюктивного программирования
Up: book
Previous: IV Двойственность для несобственных
Список научных трудов Еремина И.И.
e-mail: Еремин И.И.
![]() --
функция Лагранжа, поставленная в соответствие задаче математического
программирования
--
функция Лагранжа, поставленная в соответствие задаче математического
программирования
![]() ,
,
![]() ,
, ![]() .
.
![]() дают
дают
![]() , то (1)* принимает вид
, то (1)* принимает вид
![]() ,
,
![]() (E -- единичная матрица), Qj=0,
(E -- единичная матрица), Qj=0, ![]() , то
задача (1) примет вид
, то
задача (1) примет вид
![]() (1) и, в частности,
(1) и, в частности,
![]() (8). Во избежание громоздких преобразований
ограничимся проверкой второго соотношения.
(8). Во избежание громоздких преобразований
ограничимся проверкой второго соотношения.
![]() и уравнения
и уравнения
![]() :
:
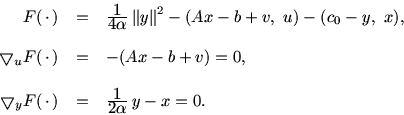
![]() , где
f0(x) = (c0,
x) -xT Q0 x, вытекает разрешимость этой задачи. В силу общей
теоремы двойственности, сформулированной выше как
утверждение 1, разрешима и задача (5), соотнесенная
к (1), причем opt(1)=opt(5). Но так как
переход от задачи (5) к задаче (1)* был эквивалентным (хотя
и сопровождавшимся исключением из записи задачи переменной x), то
равенство opt(1)=opt(1)* соблюдается.
, где
f0(x) = (c0,
x) -xT Q0 x, вытекает разрешимость этой задачи. В силу общей
теоремы двойственности, сформулированной выше как
утверждение 1, разрешима и задача (5), соотнесенная
к (1), причем opt(1)=opt(5). Но так как
переход от задачи (5) к задаче (1)* был эквивалентным (хотя
и сопровождавшимся исключением из записи задачи переменной x), то
равенство opt(1)=opt(1)* соблюдается.
![]() , то задачи
(8) и (8)* разрешимы, при этом opt(8)=opt(8)*.
, то задачи
(8) и (8)* разрешимы, при этом opt(8)=opt(8)*.
![]() , то (8)* принимает вид
, то (8)* принимает вид
![]() (:=optL) в задаче
(:=optL) в задаче
![]() , то при
, то при
![]() :
:
![\begin{picture}
% latex2html id marker 14021
(120,85)(0,0)
\put(30,25){\makebox(...
...6){\makebox(0,0)[c]{(pen)}}
\put(60,8){\makebox(0,0)[c]{Схема~1}}
\end{picture}](img1166.gif)
![]() ArgL*, то
ArgL*, то
![]() opt
opt
![]() ; с
; с
![]() и
и ![]() разъяснен выше).
разъяснен выше).