Продолжены исследования по симметричной двойственности для линейных задач последовательной и парето-последовательной оптимизации. В отличие от работ [1,2] здесь возможность неразрешимости исходных задач предполагается изначально. Намечены пути оптимальной аппроксимации несобственных задач отмеченных типов.
В работах [1,3] автор рассматривал вопросы двойственности для задач лексикографического (последовательного) и парето-последовательного программирования. Цель состояла в конструировании двойственности симметричной архитектуры, при этом исходная задача вместе с двойственной предполагались разрешимыми или, более общо, обладающими свойством собственности [1]. В работе [3] двойственность для несобственных задач линейной оптимизации рассматривалась через призму ее лексикографической интерпретации.
В данной работе рассматривается двойственность для задач паретовской и лексикографической оптимизации (Pareto-opt и lex-opt) без предположения их разрешимости, т.е. возможность неразрешимости (несобственности) исходной постановки предполагается изначально. Анализ ведется с позиций теории двойственности для несобственных задач математического программирования [2].
Выпишем три задачи:
Ниже рассматриваются вопросы симметричной двойственности (преимущественно) для задач (1) и (2) в случае их неразрешимости.
Для целей симметризации двойственности задачу (1)
поставим в параметризованном виде
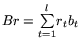 ,
r -- положительный l-мерный вектор-параметр. Наравне с
,
r -- положительный l-мерный вектор-параметр. Наравне с
Задачи (4) и (5) можно рассматривать как взаимно двойственные в смысле паретовской оптимизации. Задачи же (6) и (7) являются взаимно двойственными в классическом смысле.
Введенные множества Mr и ![]() являются
многогранниками в пространствах En и Em соответственно;
системы неравенств, их задающие, получаются путем исключения всех
переменных rt и Rj из систем
являются
многогранниками в пространствах En и Em соответственно;
системы неравенств, их задающие, получаются путем исключения всех
переменных rt и Rj из систем
![]() и
и
![]() методом Фурье-Черникова [4].
Введем также множества
методом Фурье-Черникова [4].
Введем также множества
Классификацию неразрешимых задач (4) можно провести по
альтернативным свойствам либо пары
![]() -- при
фиксированных r>0 и R>0, либо пары
-- при
фиксированных r>0 и R>0, либо пары
![]() . В
первом случае классификация такова:
. В
первом случае классификация такова:
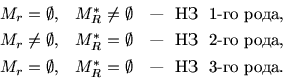
Классификацию задач (4) по свойствам пары
![]() назовем тотальной; выпишем эти
альтернативные свойства:
назовем тотальной; выпишем эти
альтернативные свойства:
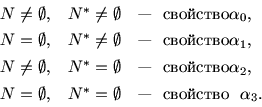
Задачи (4)-(7) свяжем естественной схемой
![\begin{displaymath}\begin{array}{rcl}
L_{\pi} & \stackrel {(1)}{\longrightarrow...
...pi,\,scal}^{\ast}\ .\\ [12pt]
& \mbox {Схема 1} &
\end{array}\end{displaymath}](img901.gif)
Требуют определенной расшифровки (интерпретации)
условия
![]() , i=0-3. Свойство
, i=0-3. Свойство
![]() означает, что
означает, что
![]() ,
,
![]() . Этот случай, как уже было
отмечено, соответствует разрешимости задач (4)-(7).
Условие
. Этот случай, как уже было
отмечено, соответствует разрешимости задач (4)-(7).
Условие ![]() означает, что при любом r>0 система
означает, что при любом r>0 система
Система ![]() несовместна тогда и только тогда, когда
совместна система
несовместна тогда и только тогда, когда
совместна система
Выделим утверждение, отвечающее разрешимости задач (4) и (5).
Теорема 1. Задачи ![]() и
и ![]() при
при
![]() одновременно разрешимы или неразрешимы; необходимым и достаточным
условием их разрешимости являются включения
одновременно разрешимы или неразрешимы; необходимым и достаточным
условием их разрешимости являются включения
![]() , при этом реализуется схема связей между ними и
задачами
, при этом реализуется схема связей между ними и
задачами
![]() :
:
![\begin{displaymath}\begin{array}{rcl}
L_{\pi} &
\stackrel {\mbox {\scriptsize\...
...\ast}_{\pi, scal}\ .\\ [12pt]
& \mbox {Схема 2} &
\end{array}\end{displaymath}](img922.gif)
Неразрешимость задачи (4), следовательно, и (5),
состоит в несовместности хотя бы одной из систем их ограничений при
r>0, R>0. Преодоление неразрешимости произвольной задачи
осуществляется путем ее аппроксимации (в том или ином смысле).
Неразрешимость систем ограничений в задаче оптимизации преодолевается
в соответствии с методом штрафных функций. Этот прием, примененный
одновременно к формально двойственной задаче, дает возможность
аппроксимации и исходной задачи в целом (т.е. не только ее системы
ограничений). Проблему аппроксимации и симметричной двойственности в
этом случае можно поставить в соответствии со схемой анализа
несобственных задач ЛП [2]. Рассмотрим вначале частный случай, а
именно. Задачам (4) и (5) поставим в соответствие
задачи по правилу (#) [2]:
Теорема 2. Задачи ![]() и
и ![]() тотально (т.е. при любых
реализациях всех их параметров) разрешимы, при этом
opt(12)=opt(13) и реализуется схема связей:
тотально (т.е. при любых
реализациях всех их параметров) разрешимы, при этом
opt(12)=opt(13) и реализуется схема связей:
![\begin{displaymath}\begin{array}{rcccc}
(4) & \stackrel {\scriptstyle {(\char93...
... & (13)_{\pi}\ ,\\ [12pt]
& & \mbox {Схема 3} & &
\end{array}\end{displaymath}](img932.gif)
Справедливость сформулированного утверждения следует из общей теоремы двойственности для НЗ ЛП ([2], теорема 6.2) и хорошо известной связи между паретовской задачей и ее скаляризующей.
Рассмотрим вариант двойственности, связанный с
отображением (4)
![]() из схемы 3 более общего
вида. С этой целью системы ограничений в задачах (4) и
(5) произвольным образом разобьем на подсистемы
из схемы 3 более общего
вида. С этой целью системы ограничений в задачах (4) и
(5) произвольным образом разобьем на подсистемы
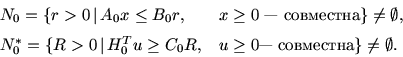
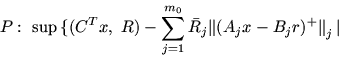
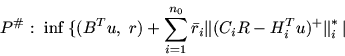
Теорема 3. Если параметры r, R и ![]() ,
, ![]() выбраны вышеуказанным образом, причем для P выполнено условие
регулярности (например, условие Слейтера), то в задачах
P и P#
выбраны вышеуказанным образом, причем для P выполнено условие
регулярности (например, условие Слейтера), то в задачах
P и P# ![]() и
и ![]() конечны, при
этом optP=optP# и реализуется схема
связей:
конечны, при
этом optP=optP# и реализуется схема
связей:
![\begin{displaymath}\begin{array}{rcccc}
L_{\pi} & \stackrel {\scriptstyle {(\ch...
...i}^{\char93 }\ ,\\ [12pt]
& & \mbox {Схема 4} & &
\end{array}\end{displaymath}](img947.gif)
Разрешимость задачи (4) связана, как было сказано, с
совместностью ограничений в задачах (4) и (5). Если эти
условия нарушаются, то коррекцию (или оптимальную коррекцию) можно
осуществить либо за счет коррекции параметров r и R,
либо за счет коррекции матриц B и C. Рассмотрим
конструкцию оптимальной коррекции (аппроксимации) матриц B и
C для обеспечения совместности систем ограничений в
задачах (4), (5), т.е. разрешимости этих задач. Пусть
![]() и
и
![]() -- приращения для матриц B и
C, рассматриваемых как векторы пространств Rn x l и
Rm x k соответственно, т.е.
-- приращения для матриц B и
C, рассматриваемых как векторы пространств Rn x l и
Rm x k соответственно, т.е.
![]() Rn x
l,
Rn x
l,
![]() Rm x k. Если ввести функцию ``качества''
этих приращений
Rm x k. Если ввести функцию ``качества''
этих приращений
![]() , то можно поставить
задачу коррекции в форме: найти
, то можно поставить
задачу коррекции в форме: найти
Рассмотрим задачу (2) в ее более общем параметрическом
варианте:
Заметим, что задачи (22) и (24) в своей исходной
постановке независимы по выбору параметров ![]() и упорядочений
и упорядочений
![]() . С Llex и
. С Llex и
![]() свяжем перекрестно скаляризующие их задачи:
свяжем перекрестно скаляризующие их задачи:
здесь
![]() .
.
Из условий разрешимости задачи ЛП следуют условия разрешимости
задач Llex и
![]() в следующих формах.
в следующих формах.
Пусть
J ={ aj, -ei }1, 1m, n, {aj}1m --
строчки матрицы A, {ei}1n -- единичные орты пространства
Rn;
![]() ,
,
![]() -- единичные орты пространства Rm. Выпишем
две группы соотношений:
-- единичные орты пространства Rm. Выпишем
две группы соотношений:
В связи с этой теоремой представляет интерес то обстоятельство,
что значения параметров r и R, обеспечивающих
справедливость сформулированной теоремы, обеспечивают ее
справедливость и в ситуации ``урезанных'' совокупностей
функций {cjTx} и {biTu}, а именно. Рассмотрим
``урезанные'' задачи
Теорема 4. Пусть системы неравенств ![]() ,
, ![]() и
и
![]() ,
, ![]() совместны для всех
совместны для всех
![]() ,
,
![]() и выполнены условия
и выполнены условия ![]() ,
, ![]() .
Тогда существует непустая область значений параметров r>0
и R > 0 -- единых для всех
.
Тогда существует непустая область значений параметров r>0
и R > 0 -- единых для всех
![]() и
и
![]() и таких, что
и таких, что
| (33) |
Дадим пояснения к обоснованию сформулированной
теоремы. Обоснование для случая задач (22), (24) и
(25), (26) в соответствии с работой [2,
теорема 2.1] состоит в последовательном назначении констант:
![]() -- для обеспечения эквивалентности (по Arg)
задач (23)k-1 и
-- для обеспечения эквивалентности (по Arg)
задач (23)k-1 и
![]() , затем
, затем ![]() -- для
обеспечения эквивалентности задач (23)k-2 и
-- для
обеспечения эквивалентности задач (23)k-2 и
![]() и т.д., наконец,
и т.д., наконец, ![]() --
для обеспечения эквивалентности задач (23)0 и
--
для обеспечения эквивалентности задач (23)0 и
![]() .
При этом назначение констант не зависит от r [2,
лемма 2.1]. Значения параметров Rj, фигурирующих в
формулировке теоремы 4, получаются в силу соотношений
.
При этом назначение констант не зависит от r [2,
лемма 2.1]. Значения параметров Rj, фигурирующих в
формулировке теоремы 4, получаются в силу соотношений
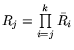 . Так же дело обстоит и с
назначениями параметров ri. Из описанной схемы формирования
Rj и ri видно, что эти же константы обслуживают
схему эквивалентной сводимости задач (29), (31) к
задачам (30), (32), что и является смыслом
теоремы 4.
. Так же дело обстоит и с
назначениями параметров ri. Из описанной схемы формирования
Rj и ri видно, что эти же константы обслуживают
схему эквивалентной сводимости задач (29), (31) к
задачам (30), (32), что и является смыслом
теоремы 4.
Неразрешимость задачи (22) состоит либо в несовместности системы ее ограничений (при заданном r), либо в невыполнимости одного из включений (27). Так же дело обстоит и с неразрешимостью задачи (24): либо ее система ограничений несовместна (при заданном k), либо не выполняется одно из включений (28). Включения (27) и (28) могут быть эквивалентно записаны в форме последовательностей систем линейных неравенств:
Рассмотрим первую систему из (34), т.е. ![]() ,
,
![]() . Нарушение первого включения из (27) означает
несовместность последней. Вектором невязки для нее будет
(ck -
ATu)+, где ``+'' над вектором означает замену его отрицательных
координат нулями (положительная срезка). Если в силу некоторой нормы
. Нарушение первого включения из (27) означает
несовместность последней. Вектором невязки для нее будет
(ck -
ATu)+, где ``+'' над вектором означает замену его отрицательных
координат нулями (положительная срезка). Если в силу некоторой нормы
![]() определить уклонение
определить уклонение
![]() и
и
![]() , то вектор
, то вектор
![]() будет минимальной (по критерию введенной нормы
будет минимальной (по критерию введенной нормы
![]() )
коррекцией вектора ck, обеспечивающей совместность системы
)
коррекцией вектора ck, обеспечивающей совместность системы
![]() , или (что одно и то же) выполнение
включения
, или (что одно и то же) выполнение
включения
![]() cone
cone![]() при
при
![]() . Подставив во вторую систему из (34)
. Подставив во вторую систему из (34) ![]() вместо ck, аналогично подсчитаем
вместо ck, аналогично подсчитаем ![]() путем
введения для вектора-невязки своей нормы
путем
введения для вектора-невязки своей нормы
![]() и
т.д.
и
т.д.
Если в качестве вводимых выше норм брать монотонные кусочно-линейные нормы, то все задачи коррекции преобразуются в задачи линейного программирования.
Сделаем еще одно замечание: выполнимость соотношений (27),
(28) эквивалентна
тому, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() в приведенной схеме
оптимальной коррекции.
в приведенной схеме
оптимальной коррекции.
Соотношения (27), (28), как необходимые условия
разрешимости задач Llex и
![]() при
рассмотрении двойственности, будем считать выполненными. Как
показано, выполнимость их решается процедурой последовательной
оптимальной коррекции.
при
рассмотрении двойственности, будем считать выполненными. Как
показано, выполнимость их решается процедурой последовательной
оптимальной коррекции.
Вопрос о преодолении несовместности систем ограничений в
(22) и (24) (при всех или некоторых r>0 и
R>0) может быть решен в рамках схемы двойственности для
несобственных задач оптимизации. Системы
![]() и
и
![]() разобьем произвольным
образом на подсистемы:
разобьем произвольным
образом на подсистемы:
По исходным задачам (22) и (24), а также разбиениям
(36) и (37), сконструируем следующие задачи
лексикографической оптимизации:
Задачи (39) и (40) синтезируют смысл последовательной аппроксимации несовместных ограничений задач (22), (24) и исходной последовательной оптимизации упорядоченных систем линейных функций {ciTx}1k и {bjTu}1l.
Следующий шаг состоит в двойной перекрестной скаляризации этих
задач, а именно:
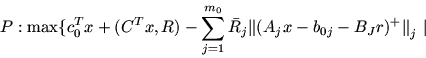
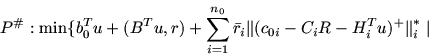
Сразу же отметим, что основная нацеленность в изучении задач
(34), (40) и (43), (44) состоит в обеспечении
реализации схемы:
![\begin{displaymath}\begin{array}{rcc}
(39) & \stackrel {\mbox {\scriptsize\mbox...
...ightarrow }}
& (44),\\ [12pt]
& \mbox {Схема 5} &
\end{array}\end{displaymath}](img1076.gif)
Сформулируем ряд утверждений, подготовляющих доказательство теоремы 5. Для полноты приводится лемма из работы [1, лемма 2.2].
Лемма 1. Для разрешимой задачи
![\begin{displaymath}\max\nolimits_p\left\{ \left [
\begin{array}{c}c_0^Tx\\ [4pt] c_1^Tx \end{array} \right ]\ \Bigg \vert\ x\,\in\,M \right\}\end{displaymath}](img1077.gif)
Обобщением ее служит
Лемма 2. Пусть в разрешимой задаче
Д о к а з а т е л ь с т в о этой леммы
состоит в детализации доказательства леммы 1 с использованием
универсального представления кусочно-линейной нормы
![]() в виде
в виде
![]() , при этом r{cj}=k -- размерность пространства переменной
, при этом r{cj}=k -- размерность пространства переменной
![]() .
.
Эквивалентный переход от (45) к (46) состоит в применении
метода точных штрафных функций, предполагающий выполнимость условия
регулярности, которое выполняется автоматически для линейных
ситуаций. Внутри постановки (45) содержится задача
Задачу (47) можно переписать в форме линейной программы
Пусть система ![]() разбита произвольным образом на
подсистемы
разбита произвольным образом на
подсистемы
![]() , при этом подсистема
, при этом подсистема
![]() -- совместна. Выпишем задачи
-- совместна. Выпишем задачи
Лемма 3. Если нормы
![]() кусочно-линейны и
кусочно-линейны и
![]() разрешима, то выбор параметров
разрешима, то выбор параметров
![]() ,
реализующих эквивалентный переход от
,
реализующих эквивалентный переход от ![]() к
к ![]() , может
быть осуществлен независимо от реализации вектора b.
, может
быть осуществлен независимо от реализации вектора b.
Д о к а з а т е л ь с т в о проводится путем последовательного применения леммы 2.
З а м е ч а н и е. Обозначения в леммах 1-3 мы не связываем прямым образом с обозначениями в задачах (39), (40), (43) и (44), хотя сформулированные леммы подготавливают анализ перечисленных задач.
Выделим некоторые условия, необходимые для формулировки теоремы:
10. Выполняются необходимые условия (27), (28) разрешимости задач (22), (24);
20. Все нормы в (43), (44) кусочно-линейны и монотонны;
30. Подсистемы
![]() и
и
![]() совместны при любых
совместны при любых ![]() и
и ![]() .
.
Теорема 5.
1. Пусть при произвольных R>0 и r>0 выполняются
условия ![]() и
и ![]() выбраны в соответствии
выбраны в соответствии
![]() .
Тогда задачи P и P# разрешимы и их оптимальные
значения совпадают.
.
Тогда задачи P и P# разрешимы и их оптимальные
значения совпадают.
2. Если выполняются условия 10-30, то существует
непустая область значений параметров R>0 и r>0,
![]() ,
,
![]() таких, что
реализуется схема 5.
таких, что
реализуется схема 5.
Д о к а з а т е л ь с т в о.
1. Сделав в задачах (43), (44) переобозначения: b0+Br=: b, c0+Cr=: c, Bjr+b0j=: bj, c0i+CiR=: ci, Hi=: Bi, мы получим формально задачи C и C# из [3, стр. 49], для которых справедлива теорема 6.12 [3, стр. 60], что эквивалентно утверждению п. 1 сформулированной выше теоремы 5.1. Что касается условий упомянутой теоремы 6.12, то они выполняются в силу условий п. 1 теоремы 5.1.
2. Схема 5 оперирует lex-задачами (39), (40)
и (43), (44), которым присвоены символы P и
P#. После переобозначений, приведенных в начале п. 1,
последние принимают вид задач P и P# из [1, стр. 179], а
исходные задачи (39), (40) -- вид задач Pp(r),
Pq#(R). Разница между Pp(r), Pq#(R) и
(39), (40) состоит в том, что в последних lex-оптимизация осуществляется по расширительному списку функций
(41), (42) с расширительным смыслом упорядочений p и
q, соответствующим (41) и (42). Приведенные
сопоставления приводят к редукции п. 2 теоремы 5.1 к
теореме 4.1 [1, стр. 188], в нашем случае выраженной схемой 5.
Здесь уместно следующее замечание относительно сказанной редукции.
При скаляризации задач (39), (40), т.е. при реализации
переходов (39)
![]() и (40)
и (40)
![]() , выбор значений
, выбор значений
![]() и
и
![]() не зависит от
параметров r и R, в силу чего их выбор, обеспечивающий
упорядочение функций {ci}0k и {bj}0l в общем
списке упорядочений (41), (42), может осуществляться после
выбора параметров
не зависит от
параметров r и R, в силу чего их выбор, обеспечивающий
упорядочение функций {ci}0k и {bj}0l в общем
списке упорядочений (41), (42), может осуществляться после
выбора параметров
![]() и
и
![]() . В этом состоит эффект применения лемм 1 и 2.
. В этом состоит эффект применения лемм 1 и 2.
З а к л ю ч е н и е. Данную работу в определенном
смысле можно считать замыкающей в ряду тех, которые посвящены
симметричной двойственности для некоторых классов задач линейной
оптимизации, а именно, для лексикографической, паретовской и
парето-лексикографической
оптимизации в вариантах их разрешимости
(собственности) и неразрешимости (несобственности). В ней не косвенно
(как в работах [1,2]), а прямым образом допускается свойство
несобственности для исходных задач. В целом, в работах [1,2] и
данной определены основные схемы двойственности, сформулированы
теоремы двойственности, затронуты вопросы аппроксимации в случае
неразрешимости задач. Конечно, возможности обобщений
результатов здесь широкие, в частности, возможности переноса на
случай произвольного пространства и числа критериев произвольной
мощности. Для конечномерной ситуации представляет интерес дальнейшая
разработка введенной автором ![]() '-оптимизации [2, § 7],
связанной
с полиэдральной оптимизацией вообще. Под последней понимаются задачи
оптимизации кусочно-линейных
функций при ограничениях в форме систем
кусочно-линейных
неравенств без предположений выпуклости, что и
определяет их трудность. Требует нетривиальных усилий и создание
методов, обеспечивающих решение таких задач. Их теоретический анализ
наталкивается на необходимость дальнейшего развития полиэдральной
алгебры.
'-оптимизации [2, § 7],
связанной
с полиэдральной оптимизацией вообще. Под последней понимаются задачи
оптимизации кусочно-линейных
функций при ограничениях в форме систем
кусочно-линейных
неравенств без предположений выпуклости, что и
определяет их трудность. Требует нетривиальных усилий и создание
методов, обеспечивающих решение таких задач. Их теоретический анализ
наталкивается на необходимость дальнейшего развития полиэдральной
алгебры.
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ
90С25
Eremin, I.I. Duality for improper problems of Pareto
and lexicographical linear optimization. (Russian)
Trudy Inst. Mat. i Mekh. (Ekaterinburg) 4 (1996),
322-336.
Recent advances on symmetric duality for sequential and Pareto-sequential linear optimization problems are proceeded. Unlike to earlier author's works this problems may be improper (unsolvable in the usual sense). Some ways to optimal approximation of the problems are indicated.