кусочно-линейного программирования
Изучение вопросов кусочно-линейного программирования
естественным образом приводит к постановке задачи дизъюнктивного программирования. Произвольная непрерывная
кусочно-линейная функция (k-линейная функция или просто k-функция), заданная на Rn, допускает стандартное представление в
форме [1]
В схеме общей постановки пусть {Mj}1m -- произвольные
множества из Rn и f(x) -- произвольная функция, заданная
на Rn. Запишем задачи
Первую из них назовем задачей в конъюнктивной
постановке, вторую -- в дизъюнктивной. Форма (1.3)
является обычной для задач математического программирования. Вторая
из них отражает ситуацию кусочно-линейной задачи (1.2). Пусть
в (1.4):
![]() , Fj: R
, Fj: R![]() R
R
![]() ,
, ![]() . Для
задачи
. Для
задачи ![]() функцией Лагранжа является
функцией Лагранжа является
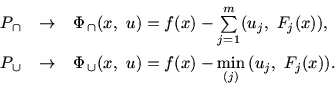
Хотя кусочно-линейные функции и соответствующий им аппарат имеют важное значение, тем не менее число работ, посвященных этим вопросам, незначительно. Отметим работы [1-6].
Пусть F0 -- некоторое линейное функциональное
пространство с вещественным пространством X значений аргумента
функций из F0. Если
![]() F0, то
функция дискретного максимума
F0, то
функция дискретного максимума
![]() может как принадлежать F0, так и не принадлежать.
Способ образования функции f(x) назовем
может как принадлежать F0, так и не принадлежать.
Способ образования функции f(x) назовем
![]() -операцией.
-операцией.
Речь пойдет о минимальном расширении пространства F0 до
линейного пространства F, обеспечивающего свойство
![]() -замкнутости:
-замкнутости:
Минимальное
![]() -замкнутое расширение назовем
-замкнутое расширение назовем
![]() -расширением. Из смысла такого расширения
видно, что
-расширением. Из смысла такого расширения
видно, что
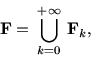
На самом деле все функции из F могут быть преобразованы к
некоторому стандартному виду. В основе такого преобразования лежит
ряд тождеств, справедливых для произвольного набора функций:
здесь
![]() ,
,
![]() ;
;
Наравне с F введем пространство
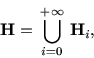
Операция взятия положительной срезки ``+'' является частным
случаем
![]() -операции, однако она потенциально (т.е. многократно
примененная) дает тот же класс функций F. Имеет место
-операции, однако она потенциально (т.е. многократно
примененная) дает тот же класс функций F. Имеет место
2) Классы ![]() и
и
![]() совпадают.
совпадают.
Д о к а з а т е л ь с т в о. 1) Соотношение ![]() означает совпадение Fk
с F1 при k>1. На самом деле достаточно доказать F2
=F1. В силу (2.4) можно ограничиться преобразованием
функции
означает совпадение Fk
с F1 при k>1. На самом деле достаточно доказать F2
=F1. В силу (2.4) можно ограничиться преобразованием
функции
![]() при
при
![]() F1 к виду (2.9). Пусть
F1 к виду (2.9). Пусть
![]() .
Доказательство можно вести индукцией по n. Если n=1, то
f(x) =
f1(x) удовлетворяет требуемому свойству представления (2.9).
Пусть n>1. Так как
.
Доказательство можно вести индукцией по n. Если n=1, то
f(x) =
f1(x) удовлетворяет требуемому свойству представления (2.9).
Пусть n>1. Так как ![]() F1, то эти функции можно
представить в виде
F1, то эти функции можно
представить в виде
Представимость функций из F в виде (2.10) или (2.11) следует из тождества (2.8).
2) Докажем вначале включение H![]() F1,
т.е. H
F1,
т.е. H![]() F1,
F1, ![]() . Если
. Если ![]() H1, то в силу (2.4):
H1, то в силу (2.4): ![]() F1. Следовательно,
H
F1. Следовательно,
H![]() F1. Пусть H
F1. Пусть H![]() F1,
докажем H
F1,
докажем H
![]() F1. Произвольная функция из Hk+1 имеет вид
F1. Произвольная функция из Hk+1 имеет вид
Обратно, если ![]() F, т.е. f имеет вид (2.9),
то, показав, что функция дискретного максимума при образующих
из F0 принадлежит H, т.е. некоторому Hk, мы тем
самым покажем и
F, т.е. f имеет вид (2.9),
то, показав, что функция дискретного максимума при образующих
из F0 принадлежит H, т.е. некоторому Hk, мы тем
самым покажем и ![]() H. Итак, пусть
H. Итак, пусть
Представления (2.9)-(2.11) функций класса F, таким образом, эквивалентны. Конструктивное доказательство этого опирается на тождества (2.3)-(2.8).
Мы уже отметили, что представление функции в форме (2.9)
может быть переписано в форме (2.10) при
fji = fj -gi
(см. (2.8)). Нужно убедиться в обратном. Итак, пусть f
вида (2.10), т.е.
![]() . Если
. Если
![]() и n=1, то
и n=1, то
![]() F1. При n>1
доказательство, как это и делалось выше, можно провести индукцией
по n. По (2.6):
F1. При n>1
доказательство, как это и делалось выше, можно провести индукцией
по n. По (2.6):
Эквивалентность представлений (2.11) и (2.9) доказывается аналогично. Теорема доказана полностью.
Функции f из F будем называть
![]() -функциями,
или
-функциями,
или
![]() -кусочными функциями. Если F0 -- пространство
линейных функций, то F -- пространство кусочно-линейных функций.
-кусочными функциями. Если F0 -- пространство
линейных функций, то F -- пространство кусочно-линейных функций.
Рассмотрим задачи (1.3) и (1.4) с их
функциями Лагранжа соответственно (1.5) и (1.6).
Задачу (1.4), в которой
![]() ,
,
![]() , можно переписать в виде
, можно переписать в виде
Если
![]() - седло функции
Лагранжа
- седло функции
Лагранжа
![]() , поставленной в
соответствие задаче
, поставленной в
соответствие задаче ![]() , то
, то
![]() ,
,
![]() и
и
![]() Arg(1.3).
Arg(1.3).
Для задачи (3.1) и ее дизъюнктивной функции
Лагранжа
![]() имеет место аналогичное
утверждение.
имеет место аналогичное
утверждение.
Д о к а з а т е л ь с т в о. В соответствии с определением седловой точки
Необходимо доказать оптимальность вектора ![]() для (3.1), т.е.
для (3.1), т.е.
![]() ,
,
![]() . Обратимся к соотношению (3.3), которое можно теперь
пареписать в виде
. Обратимся к соотношению (3.3), которое можно теперь
пареписать в виде
В математическом программировании (МП) более важной является обратная теорема, формулирующая условия, гарантирующие существование седловой точки для соответствующей функции Лагранжа. Такие теоремы имеют место для разрешимых задач линейного программирования (ЛП), выпуклого программирования (ВП) с условиями регулярности и некоторых других классов задач МП. Для дизъюнктивных постановок задач МП ситуация усложняется. В частности, усиливаются требования типа регулярности.
Задачу (3.1) назовем вполне регулярной, если каждая
из задач
Пусть
![]() --
функция Лагранжа для (3.7), здесь
--
функция Лагранжа для (3.7), здесь
![]() ,
,
![]() .
.
Несколько модифицируем функцию
![]() , а
именно, положим
, а
именно, положим
Д о к а з а т е л ь с т в о. Что касается утверждений из формулировки 1), то они
проверяются так же, как и теоремы 1 и 2.
Рассмотрим утверждение 2). Требуется доказать
З а м е ч а н и е к формулировкам теорем
1-3.
Доказанные теоремы носят довольно общий характер.
В них не уточняется, например, постановка задач (3.7). Но если,
скажем, (3.7) -- задача выпуклого программирования, то вместо
постулирования существования седла для их функций Лагранжа (в
теореме 2) можно было бы предположить разрешимость
задач (3.7) и выполнимость условия:
![]() ,
Fj(p) <0 (условие регулярности). Этим бы и гарантировалось
существование седла для
,
Fj(p) <0 (условие регулярности). Этим бы и гарантировалось
существование седла для
![]() ,
, ![]() . Что
касается случая линейной постановки задачи (3.1), то ниже дается
уточнение соответствующих теорем. Заметим, что линейный случай имеет
самостоятельный интерес в связи с актуальностью задач
кусочно-линейного программирования.
. Что
касается случая линейной постановки задачи (3.1), то ниже дается
уточнение соответствующих теорем. Заметим, что линейный случай имеет
самостоятельный интерес в связи с актуальностью задач
кусочно-линейного программирования.
Если
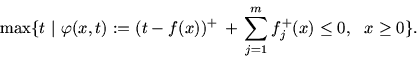
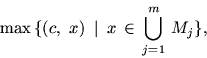
Итак, далее речь идет о задаче (3.10) и ее функции Лагранжа в
форме
Д о к а з а т е л ь с т в о. Если показать, что
![]() , то в силу теоремы 2
левое неравенство в определении седла для
, то в силу теоремы 2
левое неравенство в определении седла для
![]() будет
выполнено. Так как вектор
будет
выполнено. Так как вектор
![]() удовлетворяет одной из
систем
удовлетворяет одной из
систем ![]() , то
, то
![]() . Покажем
. Покажем
![]() . Имеем:
. Имеем:
Остается показать выполнимость правого неравенства в определении
седловой точки для
![]() , т.е.
, т.е.
Отсюда и теоремы 1 вытекает
Кусочно-линейные функции -- это
![]() -функции в
ситуации, когда F0 -- пространство линейных
функций. К определению кусочно-линейных функций
можно подойти двояко: либо так, как это только что сделано
в п. 2, либо исходя из некоторой аксиоматики, идентифицирующей
такие функции. Остановимся на втором подходе.
-функции в
ситуации, когда F0 -- пространство линейных
функций. К определению кусочно-линейных функций
можно подойти двояко: либо так, как это только что сделано
в п. 2, либо исходя из некоторой аксиоматики, идентифицирующей
такие функции. Остановимся на втором подходе.
Пусть имеются конечные совокупности многогранников { Mj }J
и собственных линейных функций
{ lj(x) }J. Будем говорить,
что система
![]() задает однозначную кусочно-линейную функцию l(x), заданную на X, если:
задает однозначную кусочно-линейную функцию l(x), заданную на X, если:
Будем использовать обозначения: L0 -- пространство линейных функций, L -- пространство k-линейных функций, определенных внешним образом в силу свойств 1) и 2). На самом деле класс функций L совпадает с классом F из предыдущего параграфа, который строится из F0 =L0, т.е. L -- это минимальное расширение пространства линейных функций, замкнутое относительно операций дискретного максимума (см. п. 2). Следовательно, представление (2.9), а также каждое из (2.10) и (2.11), являются универсальным представлением кусочно-линейных функций (далее будем говорить короче: k-функций).
Для унификации и упрощения записи k-функций, систем неравенств
из k-функций, задач кусочно-линейного программирования и т.д.
будем в дальнейшем полагать: X=Rn, тогда
Пусть
Конечная система неравенств из кусочно-линейных
функций (k-функций) может быть записана в виде
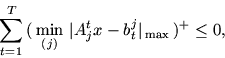
Рассмотрим представление системы в виде (4.5).
Положим
![]() . Тогда
множеством решений неравенства (4.5) будет
. Тогда
множеством решений неравенства (4.5) будет
![]() . С другой стороны, если M --
произвольное полиэдральное множество, пусть из Rn, т.е.
. С другой стороны, если M --
произвольное полиэдральное множество, пусть из Rn, т.е.
![]() и { Mj } -- многогранники:
и { Mj } -- многогранники:
![]() , то M является множеством
решений неравенства (4.5).
, то M является множеством
решений неравенства (4.5).
С этой же точки зрения посмотрим на неравенство (4.6).
Пусть
Наконец, рассмотрим систему кусочно-линейных неравенств в
форме (4.4), формально более сложную, чем (4.5) или
(4.6). Положим
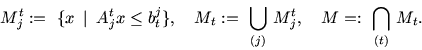
Материал, изложенный в п. 2 и п. 4, устанавливает способы конструктивного соответствия между полиэдральными множествами и их аналитическим заданием. Хотя сопутствующая этому алгебра преобразований может быть достаточно громоздкой, тем не менее логика этих преобразований проста и может быть в реальных прикладных ситуациях поручена компьютеру.
Итак, объектом рассмотрения примем задачу (5.1). Введем
частичную задачу (подзадачу)
Для k-задач выполняется ряд свойств и теорем, формулируемых в рамках теории линейного программирования. Некоторые из них являются следствиями теорем из ЛП, некоторые же требуют своих доказательств, по крайней мере, уточнений. Не требует самостоятельного доказательства
Выпишем задачу, двойственную к Lj:
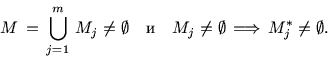
Д о к а з а т е л ь с т в о. Поскольку условия
![]() и
и
![]() являются необходимыми и достаточными для разрешимости задачи Lj,
то
являются необходимыми и достаточными для разрешимости задачи Lj,
то
![]() конечен и является значением optP. Обратно, если задача P
разрешима, то все задачи Lj c
конечен и является значением optP. Обратно, если задача P
разрешима, то все задачи Lj c
![]() разрешимы
(т.е. ситуации opt
разрешимы
(т.е. ситуации opt
![]() исключаются), а тогда
в соответствии с теоремой двойственности в ЛП:
исключаются), а тогда
в соответствии с теоремой двойственности в ЛП:
![]() ,
что и требовалось.
,
что и требовалось.
З а м е ч а н и е 5.1. Другой вариант формулировки теоремы 2 состоит в
эквивалентности
Исходную k-задачу возьмем в форме (5.1), дополнив
ее предположением (впрочем, несущественным): размерность векторов
Aj x -bj одинакова, т.е. число неравенств в каждой из систем
![]() одно и то же. Введенное условие позволяет
двойственную переменную для Lj, т.е. переменную uj в
задаче (5.4), обозначать одним символом u. В соответствии со
сказанным задачу (5.4) перепишем в виде:
одно и то же. Введенное условие позволяет
двойственную переменную для Lj, т.е. переменную uj в
задаче (5.4), обозначать одним символом u. В соответствии со
сказанным задачу (5.4) перепишем в виде:
В отношении задачи (5.6) справедлива
Д о к а з а т е л ь с т в о. Действительно, если
![]() ,
,
![]() , то для
, то для
![]() , поэтому в (5.6) максимум
можно брать только по
, поэтому в (5.6) максимум
можно брать только по ![]() . Этим и обеспечивается разрешимость
задачи P*. Необходимость условий (5.7) очевидна: если P*
разрешима, то хотя бы для одного j' задача Lj* разрешима, что
и эквивалентно (5.7).
. Этим и обеспечивается разрешимость
задачи P*. Необходимость условий (5.7) очевидна: если P*
разрешима, то хотя бы для одного j' задача Lj* разрешима, что
и эквивалентно (5.7).
Из теорем 2 и 3, а также теоремы двойственности в ЛП, вытекает
В ситуации задач P и P* свойство одновременной их
разрешимости или неразрешимости, в отличие от ЛП, теряется.
Принимая во внимание возможность несобственных оптимальных значений,
запишем эти задачи в виде
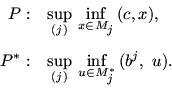
Конструкция двойственной задачи P* в
форме (5.6) подсказывается понятными соображениями,
исходящими из двойственного перехода
![]() и необходимости выполнения главного
свойства теорем двойственности в МП, а именно:
optP=optP*. Для обеспечения последнего соотношения
в P* и введена операция
и необходимости выполнения главного
свойства теорем двойственности в МП, а именно:
optP=optP*. Для обеспечения последнего соотношения
в P* и введена операция
![]() , хотя соображения симметрии требуют в двойственной
задаче иметь общую операцию
, хотя соображения симметрии требуют в двойственной
задаче иметь общую операцию ![]() (как в исходной
(как в исходной
![]() ). В этом смысле конструкция задачи P* выглядит несколько
искусственной. Здесь возможен несколько другой подход. Он связан с
известным генеральным положением относительно двойственности, когда
исходная задача записывается через свой эквивалент в форме максимина
функции Лагранжа, а тогда минимакс этой функции объявляется
объектом, двойственным к исходному. Для задач линейного
программирования это и приводит к классической двойственности. Для
пояснения можно привести схему:
). В этом смысле конструкция задачи P* выглядит несколько
искусственной. Здесь возможен несколько другой подход. Он связан с
известным генеральным положением относительно двойственности, когда
исходная задача записывается через свой эквивалент в форме максимина
функции Лагранжа, а тогда минимакс этой функции объявляется
объектом, двойственным к исходному. Для задач линейного
программирования это и приводит к классической двойственности. Для
пояснения можно привести схему:
Оказывается, что, как и в классическом случае,
максимин
дизъюнктивной функции Лагранжа, т.е.
![]() , эквивалентен исходной
задаче, которой для нас является (5.1) (она обозначена символом
P), а минимакс этой функции, т.е.
, эквивалентен исходной
задаче, которой для нас является (5.1) (она обозначена символом
P), а минимакс этой функции, т.е.
![]() , эквивалентен как раз
задаче (5.6), что будет показано ниже. Задачи (5.1) и
(5.6) допускают эквивалентную перезапись:
, эквивалентен как раз
задаче (5.6), что будет показано ниже. Задачи (5.1) и
(5.6) допускают эквивалентную перезапись:
Д о к а з а т е л ь с т в о. Пусть ![]() optLj
(=optLj*),
optLj
(=optLj*),
![]() . Очевидно,
. Очевидно, ![]() opt(5.9).
Задачу (5.12) можно переписать в эквивалентном виде
opt(5.9).
Задачу (5.12) можно переписать в эквивалентном виде
Д о к а з а т е л ь с т в о. 1. Рассмотрим внутреннюю операцию в левой
части (5.14):
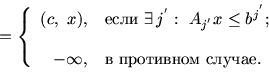
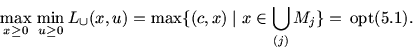
2. Выпишем внутреннюю операцию в левой части
(5.15), преобразовав очевидным образом функцию
![]() :
:
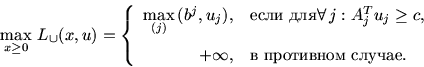
![\begin{displaymath}= \min_{u \ge 0}\, \{ \max_{(j)}\, (b^j,\ u_j)\ \mbox{$\,\mid...
... = [\,
u_1,\,...\,,u_m \,] \,\subset \, \prod_{(j)}\, M_j^* \}.\end{displaymath}](img1516.gif)
З а м е ч а н и е 5.2. На самом деле равенство из п. 1 теоремы 5 имеет место для общей постановки задачи дизъюнктивного программирования (1.4) и ее дизъюнктивной функции Лагранжа (1.6). Проверка этого аналогична предыдущему обоснованию.
Задача (5.1), к которой сводится любая задача
кусочно-линейного программирования, распадается на конечное число
параллельных задач
В аналогичных соотношениях двойственности находится и пара
задач, которая соответствует тому, что в (5.16) вместо
![]() берется
берется
![]() :
:
Отметим, что при рассмотрении двойственности в
кусочно-линейном программировании в качестве
самостоятельной выступает операция
![\begin{displaymath}\max\, \{ \min_{(j)}\,(\max) \, f_j(x_j)\ \mbox{$\,\mid\,$}\ x=[\, x_1,
\ldots\,] \,\in\,\prod_{(j)}\, M_j \},\end{displaymath}](img1531.gif)
Заметим также, что отмеченное свойство
![]() для допустимых x и u позволяет решение задач (5.1) и
(5.6) редуцировать к решению системы кусочно-линейных
неравенств
для допустимых x и u позволяет решение задач (5.1) и
(5.6) редуцировать к решению системы кусочно-линейных
неравенств
Запишем обобщения задач (5.1) и (5.6)
в форме (5.16) и (5.17), несколько изменив обозначения
нумерующих индексов, а именно: пусть
Рассмотрим ситуацию несобственности (неразрешимости) задач L
и
![]() с позиций построения двойственности. Поскольку
формально эти задачи распадаются на совокупности задач {Lk} и
{Lk*}, то к парам взаимно двойственных задач
{Lk,
Lk*}, независимо от их разрешимости или неразрешимости, можно
применить схему двойственности для несобственных задач ЛП
(см. [9, §25]):
с позиций построения двойственности. Поскольку
формально эти задачи распадаются на совокупности задач {Lk} и
{Lk*}, то к парам взаимно двойственных задач
{Lk,
Lk*}, независимо от их разрешимости или неразрешимости, можно
применить схему двойственности для несобственных задач ЛП
(см. [9, §25]):
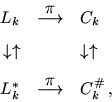
в силу которой задачи Ck и Ck# разрешимы,
при этом optCk=optCk#. Задачи Ck и
Ck# в полном соответствии с [8, § 6] имеют вид:
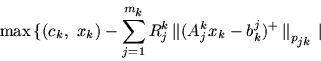
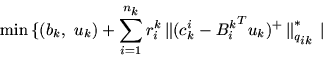
В основу двойственности для L и
![]() может быть
положена схема:
может быть
положена схема:
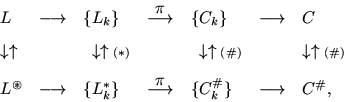
при этом формирование задач C и C# в данной схеме производится по логике формирования задач (6.1) и (6.2) из задач {Lk} и {Lk*}.
Пусть gk(xk) и gk#(uk) -- целевые функции в
задачах (6.3) и (6.4), Nk и Nk# --
допустимые множества этих задач;
![]() ,
,
![]() .
Сформируем задачи:
.
Сформируем задачи:
![\begin{displaymath}\begin{array}{rl}
C: & \sup\,\{ g(x)\ \mbox{$\,\mid\,$}\ x=[...
...,] \,\in\,
N^{\char93 }:=\ \prod\,N_k^{\char93 }\}.
\end{array}\end{displaymath}](img1567.gif)
1. Параметры rik и Rjk выбраны так, что системы
ограничений в ![]() и
и ![]() совместны при строгих
неравенствах
совместны при строгих
неравенствах
![]()
![]() и
и
![]()
![]() .
.
2. Все нормы, участвующие в формировании задач {Ck} и {Ck#}, монотонны.
3. Операция ![]() в C достижима (ее конечность
следует из условия 1 в силу свойства
в C достижима (ее конечность
следует из условия 1 в силу свойства
![]() ,
,
![]() .
.
Тогда задача C# разрешима, при этом
![]() .
.
Справедливость данного утверждения следует из основной теоремы двойственности для несобственных задач ЛП, на которую уже была ссылка выше, и тех соображений, которые легли в основу обоснования теоремы 4.
З а м е ч а н и е 6.1. Теорема 1 соотнесена к задаче довольно общего вида, содержит много параметров с широким диапозоном их выбора (разбиения систем ограничений на подсистемы, выбор норм, назначение числовых параметров Rjk и rik). Поэтому она допускает много частных формулировок, имеющих и самостоятельный интерес. Этот вопрос здесь детально не рассматривается, так как несколько уводит от основных акцентов данной статьи.
Рассмотрим общую задачу кусочно-линейного
программирования в канонической постановке (5.1), т.е.
Как и в предыдущем параграфе, будем использовать следующие
обозначения: Lj -- это задача
![]()
![]() ,
, ![]() , Lj* -- двойственная к
ней,
, Lj* -- двойственная к
ней, ![]() argLj*,
argLj*,
![]() ,
,
![]()
![]() .
.
Д о к а з а т е л ь с т в о. Обозначим целевую функцию в (7.2)
через
![]() , а вычитаемую из
, а вычитаемую из ![]() часть -- через
часть -- через
![]() . Докажем вначале равенство (7.3). Для
. Докажем вначале равенство (7.3). Для
![]() Arg(7.1) получаем
Arg(7.1) получаем
![]() opt(7.1), следовательно,
opt(7.2)
opt(7.1), следовательно,
opt(7.2)
![]() opt(7.1).
opt(7.1).
Докажем обратное неравенство. По теореме 2:
Конструкция доказательства может быть повторена для более общей
ситуации, а именно для задачи (3.1) и эквивалентной редукции ее
к задаче
Действительно, в соответствии с теоремой 2 можно
выписать неравенство
Задача разделимости непересекающихся множеств M и
N из некоторого пространства X с помощью функции f(x) из
фиксированного класса ![]() называется задачей
дискриминации множеств. Функция f(x) в этом случае называется
дискриминантной. Разделимость состоит в выполнимости
неравенств
называется задачей
дискриминации множеств. Функция f(x) в этом случае называется
дискриминантной. Разделимость состоит в выполнимости
неравенств
Если M и N -- выпуклые многогранники, а ![]() -- класс аффинных функций, то говорят о задаче линейной
дискриминации. Задача линейной дискриминации является одной из
важнейших задач в распознавании образов (РО). В качестве одной из
базовых формальных моделей РО является система строгих линейных
однородных неравенств. Убедимся в этом.
-- класс аффинных функций, то говорят о задаче линейной
дискриминации. Задача линейной дискриминации является одной из
важнейших задач в распознавании образов (РО). В качестве одной из
базовых формальных моделей РО является система строгих линейных
однородных неравенств. Убедимся в этом.
Пусть ![]() и
и ![]() -- некоторые образы,
-- некоторые образы,
![]() Rn и
Rn и
![]() Rn --
формализованные конечные выборки представителей этих образов. Если
{fs(x)}1k -- некоторый базовый набор функций (вообще говоря,
произвольный), то разделяющую функцию можно искать в виде
Rn --
формализованные конечные выборки представителей этих образов. Если
{fs(x)}1k -- некоторый базовый набор функций (вообще говоря,
произвольный), то разделяющую функцию можно искать в виде
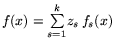 , где {zs} -- числовые
коэффициенты. Свойство разделимости состоит в выполнимости системы
неравенств:
, где {zs} -- числовые
коэффициенты. Свойство разделимости состоит в выполнимости системы
неравенств:
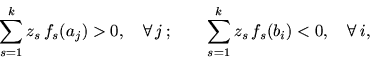
Если
![]() --
некоторое решение системы (8.2), то функция
--
некоторое решение системы (8.2), то функция
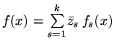 будет строго разделяющей множества A и
B. Дискриминантная функция f(x) реализует правило соотнесения
(по свойству принадлежности одному из образов
будет строго разделяющей множества A и
B. Дискриминантная функция f(x) реализует правило соотнесения
(по свойству принадлежности одному из образов ![]() и
и
![]() ) предъявляемого для распознавания вектора y по правилу:
) предъявляемого для распознавания вектора y по правилу:
Функция f(x) реализует решающее правило.
Система (8.2) может быть как совместной, так и несовместной.
На случай несовместности имеется обобщение понятия решения как
конечной совокупности векторов
![]() Rn
(именуемой комитетным решением), такой, что любое из
неравенств системы (8.2) удовлетворяется более чем половиной
векторов этой совокупности. Комитетная технология и ее использование
в задачах распознавания составляют важное и хорошо разработанное
направление в распознавании образов [10].
Rn
(именуемой комитетным решением), такой, что любое из
неравенств системы (8.2) удовлетворяется более чем половиной
векторов этой совокупности. Комитетная технология и ее использование
в задачах распознавания составляют важное и хорошо разработанное
направление в распознавании образов [10].
Если M и N -- многогранники, причем
![]() , то эти множества строго разделяются аффинной функцией.
Ниже речь пойдет о разделимости произвольных непересекающихся
полиэдральных множеств кусочно-линейной функцией (k-функцией).
, то эти множества строго разделяются аффинной функцией.
Ниже речь пойдет о разделимости произвольных непересекающихся
полиэдральных множеств кусочно-линейной функцией (k-функцией).
Итак, пусть
![]() ,
,
![]() , {Mj} и {Ni} --
конечные совокупности выпуклых многогранников, причем
, {Mj} и {Ni} --
конечные совокупности выпуклых многогранников, причем
![]() . Имеет место
. Имеет место
Д о к а з а т е л ь с т в о. Полиэдральное множество может быть задано одним
k-неравенством: если
![]() и
и
![]() , то
, то
Д е й с т в и т е л ь н о,
поскольку точка из Rn может быть задана конечной системой
линейных неравенств (если
![]() , то
, то
![]() ), сформулированное следствие
превращается в частный случай теоремы 1.
), сформулированное следствие
превращается в частный случай теоремы 1.
На самом деле, в данном следствии пространство, из
которого берутся точки, может быть произвольным. Сведение к
конечномерному арифметическому
пространству тривиально: достаточно взять
подпространство Ek исходного пространства, натянутое
на
совокупность
![]() ,
выделить его некоторый базис, в котором векторы aj и bi
будут представлены точками конечномерного
арифметического пространства. Если взять прямое разложение
X=Ek+H, то k-функция f(x),
разделяющая указанные совокупности точек в Ek, может быть
продолжена до k-функции
,
выделить его некоторый базис, в котором векторы aj и bi
будут представлены точками конечномерного
арифметического пространства. Если взять прямое разложение
X=Ek+H, то k-функция f(x),
разделяющая указанные совокупности точек в Ek, может быть
продолжена до k-функции ![]() , определенной на всем
пространстве X, по правилу: если
, определенной на всем
пространстве X, по правилу: если ![]() X и
X и
![]() ,
,
![]() Ek,
Ek, ![]() H,
то
H,
то
![]() .
.
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ