В статье рассматривается линейная задача оптимизации, синтезирующая оптимизацию по Парето и последовательную (лексикографическую) оптимизацию при акценте на проблему двойственности и получение соответствующих математически содержательных теорем.
Под паретовской задачей линейного программирования будем
понимать задачу характеризации (теоретической или
алгоритмической) оптимального множества Arg![]() задачи
задачи
| (1.1) |
Под задачей последовательного (лексикографического)
программирования понимается заключительная из задач
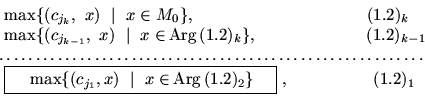
| (1.2) |
В дальнейшем вектор b будет задаваться параметрически
b=b(r), в частности, одним из следующих способов:
![]() , где
матрицы
, где
матрицы ![]() и векторы
и векторы
![]() согласованных
размеров. Этого требует обеспечение симметричной
двойственности для соответствующих задач.
согласованных
размеров. Этого требует обеспечение симметричной
двойственности для соответствующих задач.
Синтез постановок (1.1) и (1.2) реализуется в форме:
![\begin{displaymath}
\max\nolimits_{p,\pi} \left \{ \left [ \begin{array}{c}
C_...
...\end{array}\right ] \ \mid \ Ax\leq b ,\ \ x\geq0 \right \} .
\end{displaymath}](img609.gif) |
(1.3) |

![\begin{displaymath}
\max\nolimits_{p,\pi} \left \{ \left [ \begin{array}{c}
C_...
...ight ]\ \mid \ Ax\leq \sum_{i=1}^l B_i r^i,
x\geq0 \right \},
\end{displaymath}](img615.gif) |
(1.4) |
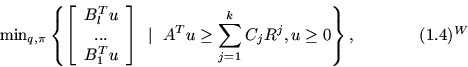
Содержательные теоремы двойственности будут
формулироваться через связь задач (1.3) и (1.3)W с
задачами, скаляризующими последние:
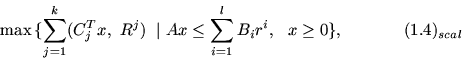
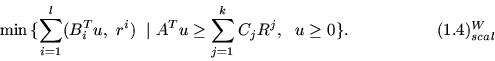
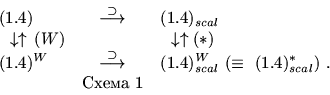
Отметим, что ![]() -задача (1.4) (
-задача (1.4) (
![]() )
)![]() трудная задача как в смысле идентификации
трудная задача как в смысле идентификации
![]() (1.4), так и (тем более!) в смысле реализации
cхемы 1. Здесь трудности принципиального свойства. Поэтому нами
будут рассматриваться отдельные типы задач названного класса.
(1.4), так и (тем более!) в смысле реализации
cхемы 1. Здесь трудности принципиального свойства. Поэтому нами
будут рассматриваться отдельные типы задач названного класса.
Задачу (1.4) назовем задачей (k, l)-типа, (1.4)W
будет иметь (l, k)-тип. Обычная задача ЛП
![]() ,
, ![]() и двойственная к ней
и двойственная к ней
![]() будут иметь (0, 0)-тип.
будут иметь (0, 0)-тип.
Выделим частный случай задач (1.4), (1.4)W, а именно:
| (1.5) |
Под многогранником M (выпуклым) будем понимать
множество решений совместной конечной системы линейных
неравенств
| (2.1) |
Множество решений (если оно не пусто) k-граничной системы [1]
| (2.2) |
Неравенство
| (2.3) |
1) неравенство (2.3)![]() следствие 1-го рода, если
существует
следствие 1-го рода, если
существует
![]() такое, что
такое, что ![]()
![]() следствие системы (2.1);
следствие системы (2.1);
2) в противном случае (2.3)![]() следствие 2-го рода.
следствие 2-го рода.
Отметим [1,2] некоторые элементарные сведения по алгебре многогранников и факты, из них вытекающие.
10. Для любого k=1,..., r, где ![]() ранг
системы
{ aj }mj=1, существует по крайней мере одна
k-грань. Если r=n, то n-грань
ранг
системы
{ aj }mj=1, существует по крайней мере одна
k-грань. Если r=n, то n-грань![]() это вершина
многогранника M.
это вершина
многогранника M.
20. Если (2.3)![]() следствие 2-го рода системы
(2.1), то
следствие 2-го рода системы
(2.1), то
![]() , где
, где
![]() . В этом
случае
. В этом
случае
![]() .
.
30. Оптимальное множество задачи ЛП является некоторой k-гранью многогранника ограничений.
40. Если
![]() ,
,
![]() ,
{ a js }s=1k линейно независимы,
то оптимальным множеством задачи
,
{ a js }s=1k линейно независимы,
то оптимальным множеством задачи
![]() является k-грань, задаваемая системой (2.2).
является k-грань, задаваемая системой (2.2).
50. Пусть
![]() конечная
совокупность
конечная
совокупность
многогранников и N =co
![]() . Если
. Если
![]() следствие 2-го рода
следствие 2-го рода
множества N (т.е.
![]() ,
,
![]() ;
;
![]() ,
,
![]() , то
, то
![]() . Это аналог
свойства 20 на случай, когда в роли исходного множества
выступает объединение конечного числа многогранников. Здесь
же отметим, что
. Это аналог
свойства 20 на случай, когда в роли исходного множества
выступает объединение конечного числа многогранников. Здесь
же отметим, что ![]() многогранник.
многогранник.
Для задачи
| (3.1) |
![\begin{picture}(60.0,40.0)(-8,0)
\put(10,10){\makebox(0,0)[r]{$(3.1)^W\hspace*{-...
...0,0)[c]{$\scriptstyle(W)$}}
\put(28,-5){\makebox(0,0)[c]{Схема~2}}
\end{picture}](img656.gif)
Эта схема реализуется при любом r>0, обеспечивающим
разрешимость задачи (3.1), что эквивалентно условиям:
1) система ![]() ,
, ![]() совместна;
2)
совместна;
2) ![]() cone{ aj}.
cone{ aj}.
Заметим, что задача (1, 0)-типа рассматривается аналогично.
Для задач
| (3.2) |
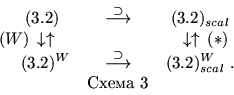
Выпишем задачи
![\begin{displaymath}
\max\nolimits_{\omega} \left \{ \left [ \begin{array}{c}
C...
...x
\end{array}\right ] \ \vert \ Ax\leq b,\ x\geq0 \right \},
\end{displaymath}](img663.gif) |
(4.1) |
Лемма 4.1 [3]. Имеет место эквивалентность (в
смысле совпадения оптимальных множеств) задач:
В этой лемме речь идет об известном факте о двухэтапной задаче последовательного программирования.
Лемма 4.2. Пусть задача (1.1) разрешима. Тогда
существует конечный набор векторов
![]() инвариантный
относительно вектора b, при котором
инвариантный
относительно вектора b, при котором
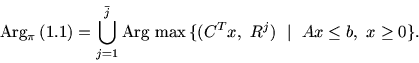
Для полноты приведем о б о с н о в а н и е
леммы. Множество
![]() (1.1) совпадает с
(1.1) совпадает с
 |
(4.2) |
Теорема 4.1. Если задача (4.1) разрешима,
то при некоторых R1>0, R2>0 имеет место включение
| (4.3) |
Д о к а з а т е л ь с т в о. В силу
леммы 4.2 и 30 из п. 2 имеем: Arg
![]() Гj, {Г
Гj, {Г![]() некоторая совокупность
некоторая совокупность
граней многогранника M0. Образуем
![]() ,
т.е. замыкание выпуклой оболочки выписанной совокупности
граней, и рассмотрим задачу
,
т.е. замыкание выпуклой оболочки выписанной совокупности
граней, и рассмотрим задачу
| (4.4) |
1) Гj выступает в качестве оптимального множества задачи
2)
![]() является оптимальным множеством
задачи
является оптимальным множеством
задачи
a) Arg
![]() Гj,
Гj,
b) Arg
![]() Гj } =Гji,
Гj } =Гji,
при этом Г![]()
![]() (4.1).
По лемме 4.1 существует
(4.1).
По лемме 4.1 существует ![]() такое, что при любом
такое, что при любом ![]()
Рассмотрим теперь задачу (2, 1)-типа:
![\begin{displaymath}
\max\nolimits_{\omega}\, \left \{ \left [ \begin{array}{c}
...
...1^Tx
\end{array}\right ]\ \mid\ Ax\leq Br,\ x\geq0 \right \}
\end{displaymath}](img701.gif) |
(4.5) |
Теорема 4.2. При любом ![]() ,
обеспечивающим совместность системы ограничений в (4.5),
из разрешимости задачи (4.5) вытекает существование R1>0
и R2>0 таких, что реализуется схема:
,
обеспечивающим совместность системы ограничений в (4.5),
из разрешимости задачи (4.5) вытекает существование R1>0
и R2>0 таких, что реализуется схема:
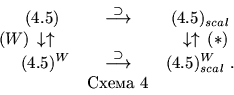
Понятно, что скаляризация задачи (4.5) осуществляется с
помощью векторных параметров R1 и R2, а скаляризация
задачи (4.5)![]() с помощью r. Верхнее включение в
схеме 4 выполняется в силу доказанной теоремы 4.1. Нижнее
включение является тривиальным.
с помощью r. Верхнее включение в
схеме 4 выполняется в силу доказанной теоремы 4.1. Нижнее
включение является тривиальным.
Еще раз подчеркнем, что правые задачи в cхеме 4 являются взаимно двойственными в классическом смысле.
Естественно, может быть сформулирован аналог теоремы 4.2
для симметричной постановки задачи, а именно, для
задачи (1, 2)-типа:
![\begin{displaymath}\min\nolimits_{\omega}\, \left \{ \left [
\begin{array}{c}B_...
...^Tu \end{array} \right ]\ \mid\ A^Tu\geq CR,\ u\geq0 \right \}.\end{displaymath}](img706.gif)
Теорема двойственности для задач (1.5) и (1.5)W будет
формулироваться через связь с задачами, скаляризующими
последние:
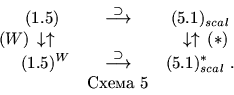
Множество {j1,..., jk } из определения k-граничной системы (2.2) назовем индексным идентификатором этой системы. Определение индексного идентификатора не зависит от реализации правых частей системы ограничений.
Применительно к внутренним задачам для (1.5) и
(1.5)W, а именно:
| (5.2) |
 |
(5.3) |
 |
(5.4) |
В силу свойства 40 из п. 2 выписанные идентификаторы
определяют те грани многогранников
![]() ,
,
![]() ,
которые выступают в качестве оптимальных множеств задач
,
которые выступают в качестве оптимальных множеств задач
| (5.5) |
| (5.6) |
В дальнейшем будут оговариваться условия,
при которых
![]() ,
,
![]() . В предположении выполнимости (5.3)
и (5.4) положим Гji:=Arg(5.5)
. В предположении выполнимости (5.3)
и (5.4) положим Гji:=Arg(5.5)
![]() ,
Г
,
Г
![]() :=Arg(5.6)
:=Arg(5.6)
![]() ,
т.е. {Гji} и {Г
,
т.е. {Гji} и {Г
![]() те совокупности граней многогранников M(ri) и
те совокупности граней многогранников M(ri) и
![]() , которые являются оптимальными множествами задач
, которые являются оптимальными множествами задач
В силу леммы 4.1 для каждого i существует j=j(i),
при котором
Характеристические множества {Rj} и {ri} назовем
равновесными, если
| (5.7) |
Теорема 5.1. Пусть задачи
![]() ,
, ![]() , i=0,1,..., k;
j=0, 1,..., l разрешимы. Для существования R>0, r>0,
реализующих схему 5, необходимо и достаточно существование
равновесных характеристических множеств.
, i=0,1,..., k;
j=0, 1,..., l разрешимы. Для существования R>0, r>0,
реализующих схему 5, необходимо и достаточно существование
равновесных характеристических множеств.
Д о к а з а т е л ь с т в о. Положим
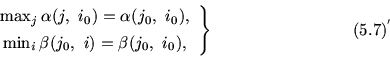
Условия (5.7) и необходимы. Действительно, если при
некоторых
![]() и
и
![]() реализуется схема 5, то положим
реализуется схема 5, то положим
![]() ,
,
![]() . Дополним эти векторы до полных
характеристических множеств { Rj }, { ri }. Тогда
по смыслу включений в схеме 5 получаем соотношения (5.7) (или
(5.7)', что одно и то же).
. Дополним эти векторы до полных
характеристических множеств { Rj }, { ri }. Тогда
по смыслу включений в схеме 5 получаем соотношения (5.7) (или
(5.7)', что одно и то же).
Далее будет рассмотрен вариант теоремы 5.1, относящийся к
ситуации неразрешимости (несобственности) задачи линейного
программирования:
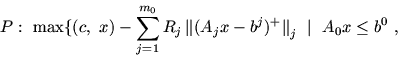
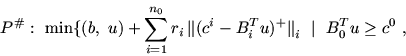
![\begin{displaymath}
A=\left [ \begin{array}{c}
A_0\\ .\ .\ .\ \\ A_{m_0}
\end{array}\right ] =[B_0\ .\ .\ .\ B_{n_0} ];
\end{displaymath}](img760.gif) |
(6.1) |
Заметим, что в задачах P и P# подсистемы
![]() ,
, ![]() и
и
![]() ,
, ![]() предполагаются совместными (выбор таких совместных подсистем
из систем
предполагаются совместными (выбор таких совместных подсистем
из систем ![]() ,
, ![]() и
и ![]() ,
, ![]() всегда можно обеспечить; например, в содержательном плане:
эти подсистемы
всегда можно обеспечить; например, в содержательном плане:
эти подсистемы![]() набор согласованных директивных
требований).
набор согласованных директивных
требований).
Для более компактной записи последующих задач введем
обозначения:
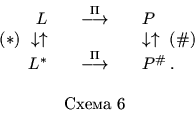
Сформулируем задачи
В описанной ситуации схема 5 принимает вид:

Теорема 6.1. Пусть в задачах P и
P# все нормы
![]() кусочно-линейны и монотонны. Тогда
кусочно-линейны и монотонны. Тогда
1) При любом ![]() , обеспечивающем совместность
системы ограничений в задаче P, существует
, обеспечивающем совместность
системы ограничений в задаче P, существует
![]() такое, что имеет место верхнее включение в схеме 7.
такое, что имеет место верхнее включение в схеме 7.
2) При любом ![]() , обеспечивающем совместность
системы ограничений в задаче P#, существует
, обеспечивающем совместность
системы ограничений в задаче P#, существует
![]() такое, что имеет место нижнее включение в схеме 7.
такое, что имеет место нижнее включение в схеме 7.
3) Схема 7 реализуется при некоторых ![]() и
и
![]() тогда и только тогда, когда для задач
тогда и только тогда, когда для задач ![]() и
и
![]() существует равновесное характеристическое
множество.
существует равновесное характеристическое
множество.
П о я с н е н и я к д о к а з а т
е л ь с т в у. Ситуация с задачами из схемы 7
отличается от ситуации схемы 5 тем, что в схеме 7 задачи
формируются из выпуклых кусочно-линейных функций, в схеме 5
![]() из линейных. Но, в принципе, первый случай сводим
ко второму (т.е. ранее рассмотренному). Эту редукцию мы и
опишем. Заметим, что произвольная выпуклая кусочно-линейная
функция имеет универсальное представление в виде
из линейных. Но, в принципе, первый случай сводим
ко второму (т.е. ранее рассмотренному). Эту редукцию мы и
опишем. Заметим, что произвольная выпуклая кусочно-линейная
функция имеет универсальное представление в виде
![]() при линейных lj(x). Зафиксируем необходимые
представления:
при линейных lj(x). Зафиксируем необходимые
представления:
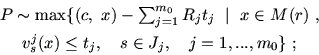 |
(6.2) |
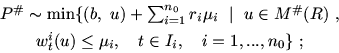 |
(6.3) |
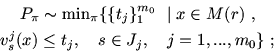 |
(6.4) |
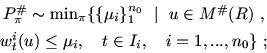 |
(6.5) |
| (6.6) |
| (6.7) |
Выписанные эквивалентности имеют ясный смысл, поэтому
пояснения мы опускаем. Задачи (6.2)-(6.7) линейные. К
ним применима схема доказательства теоремы 5.1. Следует
только обратить внимание на необходимость (и возможность) при
выборе параметров R и r обеспечить непустоту множеств
M(r) и M#(R). Это достигается тем, что при выборе
R=R0Rj0 и r=r0ri0 по схеме доказательства
теоремы 4.1 (а она и лежит в основе обоснования теоремы 5.1)
R0 можно взять как угодно
большим, т.е. если годится
![]() , то годится и любое
, то годится и любое
![]() . Этим и
обеспечивается совместность систем
. Этим и
обеспечивается совместность систем ![]() ,
, ![]() ,
,
![]() , i=1,..., n0 и
, i=1,..., n0 и
![]() ,
, ![]() ,
,
![]() , j=1,..., m0, т.е.
, j=1,..., m0, т.е.
![]() и
и
![]() .
.
З а м е ч а н и е. В теоремах 5.1 и 6.1
фигурирует условие существования равновесного
характеристического множества. Естественно, представляют
интерес достаточные для этого условия или выделение случаев,
когда условие существования равновесного характеристического
множества вообще можно снять. Приведем пример такого рода.
Частной реализацией задач P и P# для случая, когда
![]() несобственная задача 1-го рода, является [5]
несобственная задача 1-го рода, является [5]
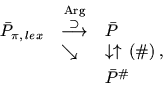
Аналогичная ситуация возникает и для случая, когда ![]() несобственная задача 2-го рода [5].
несобственная задача 2-го рода [5].
Принципиальная трудность анализа общей постановки задачи
(1.3), тем более (1.4) и (1.4)W, состоит в сложном и
плохо описываемом строении последовательности тех множеств,
на которых определяется операция ![]() в задачах
(1.3)k-(1.3)1. Эти множества в общем случае не
являются ни выпуклыми, ни замкнутыми, хотя и со свойством
полиэдральности. Напрашивается мысль о некотором сужении
в задачах
(1.3)k-(1.3)1. Эти множества в общем случае не
являются ни выпуклыми, ни замкнутыми, хотя и со свойством
полиэдральности. Напрашивается мысль о некотором сужении
![]() -оптимизации, позволяющей идентифицировать
отмеченную последовательность допустимых множеств и вносить
определенный конструктивизм в их описание.
-оптимизации, позволяющей идентифицировать
отмеченную последовательность допустимых множеств и вносить
определенный конструктивизм в их описание.
В сущности, конструкция такого сужения была продемонстрирована в доказательстве теоремы 4.1.
Формализуем эту конструкцию.
Пусть
![]() полиэдральное множество,
являющееся объединением конечного числа многогранников Mj,
j=1,..., m.
полиэдральное множество,
являющееся объединением конечного числа многогранников Mj,
j=1,..., m.
Выпишем задачу
| (7.1) |
| (7.2) |
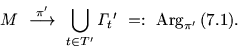
Таким образом, мы приходим к новой постановке задачи
паретовской оптимизации, а именно, ![]() -оптимизации:
-оптимизации:
З а м е ч а н и е. Если множество M является
выпуклым многогранником
![]() , то задачи (7.1) и (7.1)' совпадают.
, то задачи (7.1) и (7.1)' совпадают.
Действительно,
![]() ,
Arg
,
Arg![]() (7.1)' =
(7.1)' =
![]() Arg
Arg
![]() при M=M0, где
при M=M0, где
![]() грани многогранника M0, объединение которых
составляет паретовское множество задачи (7.1) при M=M0.
грани многогранника M0, объединение которых
составляет паретовское множество задачи (7.1) при M=M0.
Новое понятие ![]() -оптимизации может быть перенесено
и на общую постановку (1.3) в записи:
-оптимизации может быть перенесено
и на общую постановку (1.3) в записи:
![\begin{displaymath}
\max\nolimits_{\omega '}\, \left \{ \left [ \begin{array}{c...
...x
\end{array}\right ] \ \mid\ Ax\leq b,\ \ x\geq0 \right \},
\end{displaymath}](img837.gif) |
(7.3) |
Скаляризующая задача будет иметь вид:
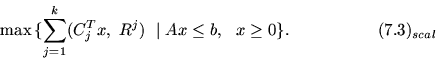
Как уже отмечалось, попытка сужения ![]() -оптимизации
связана с желанием сделать допустимые множества последовательности
задач (1.3)s идентифицируемыми посредством определенных понятий. В
этом смысле допустимые множества задач (1.3)s допускают ясную
характеристику. Имеет место
-оптимизации
связана с желанием сделать допустимые множества последовательности
задач (1.3)s идентифицируемыми посредством определенных понятий. В
этом смысле допустимые множества задач (1.3)s допускают ясную
характеристику. Имеет место
Лемма 7.1. Множество Arg
![]() является объединением некоторой совокупности
граней многогранника
является объединением некоторой совокупности
граней многогранника
![]()
![]() .
.
Д о к а з а т е л ь с т в о. Доказательство будем вести индукцией по числу компонент CTjx в целевом векторе задачи (7.3). При k=1 справедливость доказываемой леммы вытекает из леммы 4.2.
Выпишем задачу
![\begin{displaymath}
\max\nolimits_{\omega '} \left \{ \left [ \begin{array}{c}
...
... ...\\ C_2^Tx
\end{array}\right ]\ \mid\ x\in M_0 \right \}.
\end{displaymath}](img843.gif) |
(7.4) |
Теорема 7.1. Пусть задача (7.3)
разрешима. Тогда существует непустое множество
значений векторных параметров Rj>0, при которых
| (7.5) |
Д о к а з а т е л ь с т в о будем вести
индукцией по числу компонент CTjx в целевом векторе
задачи (7.3). Поскольку задача (7.1)' совпадает, как было
отмечено, с (7.1), то при k=1 включение (7.5) справедливо
при любом R>0, при этом его левая часть является одной из
граней многогранника M0. Пусть утверждение справедливо
для задачи
![\begin{displaymath}
\max\nolimits_{\omega '} \left \{ \left [ \begin{array}{c}
...
......\\ C_2^Tx
\end{array}\right ]\ \mid \ x\in M_0 \right \},
\end{displaymath}](img857.gif) |
(7.6) |
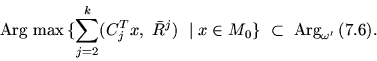 |
(7.7) |
Множество M:=Arg![]() (7.6) состоит (по лемме
7.1) из граней многогранника M0, и максимизируемый
функционал f(x) из (7.7) определяет одну из них, пусть
Г = Arg(7.7). Так как
(7.6) состоит (по лемме
7.1) из граней многогранника M0, и максимизируемый
функционал f(x) из (7.7) определяет одну из них, пусть
Г = Arg(7.7). Так как
З а м е ч а н и е. Из доказательства теоремы видно, что на самом деле ее можно формулировать в следующем виде:
Существует конечный набор скаляризующих задачу (7.3)
векторных параметров
![]() ,
таких, что объединение граней
многогранника M0, определяемых функционалами
,
таких, что объединение граней
многогранника M0, определяемых функционалами
![]() , совпадает с
Arg
, совпадает с
Arg![]() (7.3).
(7.3).
При обосновании теоремы в такой формулировке необходимо
было бы сделать аналогичное индуктивное предположение
относительно задачи (7.6), а в последующем вместо граней
Г и Г![]() рассмотреть всю
совокупность граней Гs и Г
рассмотреть всю
совокупность граней Гs и Г![]() с непустым пересечением Г
с непустым пересечением Г![]() Г
Г![]() ,
и для каждой такой ситуации определить
параметр Rst, функцию fst(x) и определяемую ею
грань. Объединение последних дает Arg
,
и для каждой такой ситуации определить
параметр Rst, функцию fst(x) и определяемую ею
грань. Объединение последних дает Arg![]() (7.3).
(7.3).
СПИСОК ЦИТИРОВАННОЙ ЛИТЕРАТУРЫ
90С25
Eremin, I.I.
The duality for Pareto-successive linear
optimization problems. (Russian)
Trudy Inst. Mat. i Mekh. (Ekaterinburg) 3 (1994),
245-260.
The linear optimization problem is regarded which is the synthesis of the Pareto optimization and lexicographical optimization formulations.
The main article point is the theory of duality and corresponding mathematical theorems.