2. Синтез управления

При синтезе управления используем рассмотренный в работе $[3]$ алгоритм построения гарантированного управления с учетом специфики свойства стабильности $(1.11)$.

Обозначим через $\varepsilon (t,z)$ нижнюю грань чисел $\varepsilon \geq 0$, для которых выполнено включение

$$e\in W(t, z-\varepsilon u+\varepsilon U(t,z)+\varepsilon S), \quad при u\in U(t,z).$$ (2.1)

Если это включение не выполнено при любом $\varepsilon \geq 0$, то полагаем $\varepsilon (t,z)=+\infty$. Если $\varepsilon (t,z)<+\infty$, то из условий $1$ и $5$ следует, что включение $(2.1)$ выполнено при $\varepsilon = \varepsilon (t,z)$.

Обозначим $U_{0}(t,z)=U(t,z)$ при $\varepsilon (t,z)=+\infty$. В противном случае, обозначим через $U_{0}(t,z)$ множество тех точек $u\in U(t,z)$, для каждой из которых выполнено включение $(2.1)$. Возьмем любое управление

$$u(t,z)\in U_{0}(t,z).$$ (2.2)

Зафиксируем разбиение $(1.4)$ и для управления $(2.2)$ построим ломаную $(1.6)$. Обозначим $z_{\omega }(t_{i})=z_{i}, \, \varepsilon_{i}=\varepsilon (t_{i},z_{i}), \, a_{i... ...epsilon_{i}), \, N_{i}=N(t_{i+1},t_{i},\varepsilon_{i})\, u_{i}=u(t_{i},z_{i})$.

Теорема 2.1. Пусть начальное состояние таково, что $\varepsilon _{0}<+\infty$. Тогда управление $(2.2)$ обеспечивает для любой ломаной $(1.6)$ выполнение включения

$$e \in W(t_{i},z_{i}+\varepsilon _{i}U_{\ast }(t_{i},\varepsilon _{i})+\varepsilon _{i}S).$$ (2.3)

Причем

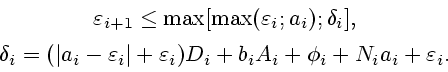$$\begin{array}{c} \varepsilon _{i+1} \leq \max [\max(\varepsi... ...+b_{i}A_{i}+\phi _{i}+N_{i}a_{i} + \varepsilon_{i}. \end{array}$$ (2.4)

Д о к а з а т е л ь с т в о. Пусть $\varepsilon _{i}<+\infty$ при $i\geq 0$. Тогда из $(2.1)$ следует, что существуют точки $u\in U(t_{i},z_{i}), \, s\in S$ такие, что

$$e\in W(t_{i},z_{\ast }), \quad z_{\ast }=z_{i}+\varepsilon _{i}(u - u_{i}+s).$$ (2.5)

Из включения $(1.13)$ следует, что помеха $v_{i}\in V(t_{i+1},t_{i},z_{i})$ представима в следующем виде:

$$v_{i}=v+A_{i}s_{i}, \quad v\in V(t_{i+1},t_{i},z_{\ast }), \, s_{i}\in S.$$ (2.6)

Из включения $(2.5)$ и из условия стабильности $(1.11)$ следует, что существуют точки

$$u_{\ast }=P(t_{i+1},t_{i},z_{\ast }), \quad s_{\ast }\in S,$$ (2.7)

такие, что $e\in W(t_{i+1},z_{\ast }-a_{i}u_{\ast }+b_{i}v+\phi _{i}s_{\ast })$. Используя равенство $z_{i+1}=z_{i}-a_{i}u_{i}+b_{i}v_{i}$, получим

$$e\in W(t_{i+1},z_{i+1}+(a_{i}-\varepsilon _{i})u_{i}+\vareps... ...\ast } +\varepsilon _{i}s-b_{i}A_{i}s_{i}+\phi _{i}s_{\ast }).$$ (2.8)

Из включений $(1.14)$ и $(2.7)$ следует, что $u_{\ast }\in U(t_{i+1},z_{i+1})+N_{i}S$. Далее, как следует из включения $(1.12)$, точки $u_{i}$ и $u$ принадлежат множеству $U(t_{i+1},z_{i+1})+D_{i}S$. Поэтому

$$(a_{i}-\varepsilon _{i})u_{i}+\varepsilon _{i}u-a_{i}u_{\ast... ...}+\varepsilon _{i}u^{(0)}-a_{i}u^{\ast }+\delta _{i}s^{\ast };$$

$$u^{(i)}, u^{(0)}, u^{\ast }\in U(t_{i+1},z_{i+1}).$$

Таким образом, включение $(2.8)$ примет вид

$$e\in W(t_{i+1},z_{i+1}+(a_{i}-\varepsilon _{i})u^{(i)}+\varepsilon _{i}u^{(0)} -a_{i}u^{\ast }+\delta _{i}s^{\ast }).$$ (2.9)

Определим $m_{i}=\max(\varepsilon _{i};a_{i})$ и покажем, что

$$e\in W(t_{i+1},z_{i+1}+m_{i}u_{+}-m_{i}u^{+}+\delta _{i}s^{\ast }); \quad u_{+},u^{+}\in U(t_{i+1},z_{i+1}).$$ (2.10)

Пусть $a_{i}\geq \varepsilon _{i}$. Тогда включение $(2.10)$ следует из включения $(2.9)$ при

$$u_{+}=a_{i}^{-1}(a_{i}-\varepsilon _{i})u^{(i)}+a_{i}^{-1}\varepsilon _{i}u^{(0)}, \quad u^{+}=u^{\ast }.$$

Пусть $a_{i}<\varepsilon _{i}$. Тогда включение $(2.10)$ выполнено при

$$u_{+}=u^{0}, \quad u^{+}=\varepsilon _{i}^{-1}(\varepsilon _{i}-a_{i})u^{(i)}+ \varepsilon ^{-1}_{i}a_{i}u^{\ast }.$$

Отметим, что в обоих случаях точки $u_{+}$ и $u^{+}$ принадлежат выпуклому множеству $U(t_{i+1},z_{i+1})$.

Рассмотрим включение $(2.10)$. Пусть $m_{i}\leq \delta _{i}$. Тогда

$$m_{i}u_{+}-m_{i}u^{+}=\delta _{i}u_{+}-\delta _{i}u, \quad u ... ...a _{i}^{-1}(\delta _{i}-m_{i})u_{+}+\delta _{i}^{-1}m_{i}u^{+}.$$

Отсюда, используя определение числа $\varepsilon _{i+1}$, получим неравенство $\varepsilon _{i+1}\leq \delta _{i}$.

Пусть $m_{i}>\delta _{i}$. Тогда $\delta _{i}s^{\ast }=m_{i}s, \, s=m_{i}^{-1}\delta _{i}s^{\ast }\in S$. Отсюда и из определения числа $\varepsilon _{i+1}$ получим неравенство $\varepsilon _{i+1}\leq m_{i}$.

Таким образом, $\varepsilon _{i+1}\leq \max(m_{i};\delta _{i})$. Подставляя сюда значение $m_{i}$, получим требуемое неравенство $(2.4)$.

Рассмотрим случай, когда существуют функции $L(\tau ,t)\geq 0$ и $C(\tau ,t)\geq 0$ при $t<\tau \leq p$ такие, что

$$A(\tau ,t,\varepsilon )\leq L(\tau , t)\varepsilon , \quad N(\tau ,t,\varepsilon )\leq L(\tau ,t)\varepsilon + C(\tau, t).$$ (2.11)

Тогда из формул $(2.4)$ получим оценку

$$\varepsilon _{i+1}\leq (1+\psi (t_{i+1},t_{i}))\max (\varepsilon _{i};a(t_{i+1},t_{i}))+\phi (t_{i+1},t_{i}).$$ (2.12)

Здесь обозначено

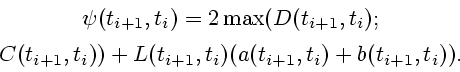$$\begin{array}{c} \psi (t_{i+1},t_{i}) = 2\max (D(t_{i+1},t_{... ...(t_{i+1},t_{i})(a(t_{i+1},t_{i})+b(t_{i+1},t_{i})). \end{array}$$ (2.13)

Определим

$$\begin{array}{c} a(\omega )=\max\limits_{0\leq i\leq k}a(t_{... ...a ) = \sum\limits_{i = 0}^{k} \psi (t_{i+1},t_{i}). \end{array}$$

Тогда из $(2.12)$ следует $[3]$ оценка

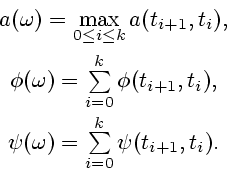
$$\varepsilon (p, z_{\omega }(p)) = \varepsilon _{k+1}\leq \Bi... ... _{0}, a(\omega ))+\phi (\omega )\Bigr] \exp (\psi (\omega )).$$ (2.14)

Следствие 2.1. Пусть $a(\omega )\rightarrow 0$ и $\phi (\omega )\rightarrow 0$ при $d(\omega )\rightarrow 0$ и существуют числа $\delta >0$ и $\psi _{\ast }> 0$ такие, что $\psi (\omega )\leq \psi _{\ast }$ для всех разбиений $\omega$ с $d(\omega ) \leq \delta$. Тогда управление $(2.2)$ гарантирует окончание $(1.7)$ из любого начального положения $e\in W(t_{0}, z_{0})$.

В самом деле, положим в $(2.14)$ $\varepsilon _{0} = 0$ и устремим $d(\omega )\rightarrow 0$. Тогда $\varepsilon (p, z_{\omega }(p))\rightarrow 0$.