В линейном нормированном пространстве ![]() происходит движение вектора
происходит движение вектора ![]() по правилу
по правилу
| (1.1) |
| (1.2) |
Считаем, что управление и помеха удовлетворяют ограничениям
| (1.3) |
Движение формализуем с помощью ломаных Эйлера. Зафиксируем начальное состояние ![]() и
рассмотрим разбиение
и
рассмотрим разбиение
| (1.4) |
Допустимым управлением является любая функция
| (1.5) |
Зафиксируем управление ![]() . Построим ломаную Эйлера
. Построим ломаную Эйлера
| (1.6) |
Сформулируем цель синтеза управления. Задано второе линейное нормированное пространство ![]() , точка
, точка ![]() и
многозначная функция
и
многозначная функция
![]() . Цель синтеза управления заключается в осуществлении
включения
. Цель синтеза управления заключается в осуществлении
включения
| (1.7) |
Мы не налагаем на множества ![]() условий, которые давали бы возможность определить
реализовавшееся в момент времени
условий, которые давали бы возможность определить
реализовавшееся в момент времени ![]() состояние
состояние ![]() , как предельную точку конечных состояний
, как предельную точку конечных состояний
![]() последовательности ломаных
последовательности ломаных ![]() при диаметре разбиения, стремящемся к нулю. Поэтому формализуем условие того,
что какое-то управление
при диаметре разбиения, стремящемся к нулю. Поэтому формализуем условие того,
что какое-то управление ![]() гарантирует в момент времени
гарантирует в момент времени ![]() включение
включение ![]() ,
не прибегая к определению предельных движений.
,
не прибегая к определению предельных движений.
Обозначим через ![]() единичный шар в
единичный шар в ![]() и через
и через
![]() алгебраическую сумму множеств
алгебраическую сумму множеств ![]() и
и ![]()
| (1.8) |
О п р е д е л е н и е 1.1. Управление ![]() гарантирует включение
гарантирует включение ![]() из начального состояния
из начального состояния ![]() , если
для любого числа
, если
для любого числа ![]() найдется число
найдется число ![]() такое, что для любой ломаной
такое, что для любой ломаной ![]() с диаметром разбиения
с диаметром разбиения
![]() выполнено включение
выполнено включение
| (1.9) |
Синтез управления будем осуществлять, опираясь на конструкцию
стабильного моста ![]() , который в
рассматриваемом случае будет
являться многозначной функцией
, который в
рассматриваемом случае будет
являться многозначной функцией
![]() , при
, при
![]() ,
удовлетворяющей граничному условию
,
удовлетворяющей граничному условию
| (1.10) |
В монографии [1, стр. 294] отмечалось, что при построении стабильных мостов можно использовать различные аппроксимационные аналоги уравнения движения.
Рассмотрим случай, когда условие стабильности записывается с помощью некоторой многозначной функции
![]() следующим образом:
следующим образом:
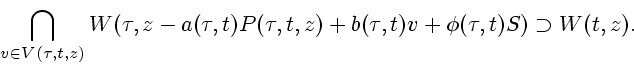 |
(1.11) |
Сформулируем условия, при которых мы будем проводить синтез управления.
Условие 1. Каждое из множеств ![]() является выпуклым компактом.
является выпуклым компактом.
Условие 2. При ![]() определена функция
определена функция
![]() такая, что для любых
такая, что для любых
![]() выполнено включение
выполнено включение
![\begin{displaymath}
U(t,z)\subset \bigcap_{u,v}\Bigl[U(\tau ,z-a(\tau ,t)u+b(\tau ,t)v)+D(\tau ,t)S\Bigl].
\end{displaymath}](img46.gif) |
(1.12) |
Условие 3. При
![]() определена функция
определена функция
![]() такая, что
при всех
такая, что
при всех
![]() выполнено включение
выполнено включение
![\begin{displaymath}
V(\tau ,t,z)\subset \bigcap_{u,v}\Bigl[ V(\tau ,t,z+\varepsilon u+\varepsilon s)+A(\tau ,t,\varepsilon )S\Bigl].
\end{displaymath}](img51.gif) |
(1.13) |
Условие 4. При
![]() определена функция
определена функция
![]() такая, что при всех
такая, что при всех
![]() выполнено включение
выполнено включение
![\begin{displaymath}
P(\tau ,t,z+\varepsilon U_{\ast }(t,z)+\varepsilon S)\subset...
...u ,z
-a(\tau ,t)u+b(\tau ,t)v)+N(\tau ,t,\varepsilon )S\Bigl].
\end{displaymath}](img54.gif) |
(1.14) |
Условие 5. Стабильный мост удовлетворяет следующему
условию замкнутости по
![]() .
.