Рассмотрим в ![]() управляемый процесс
управляемый процесс
| (3.1) |
| (3.2) |
Предполагаем, что существует число ![]() такое, что
такое, что
| (3.3) |
Считаем, что каждое из множеств
![]() при
при
![]() является компактом и содержится в шаре радиуса
является компактом и содержится в шаре радиуса
![]() , где
, где ![]() - скалярная функция, интегрируемая
на каждом отрезке; отображение
- скалярная функция, интегрируемая
на каждом отрезке; отображение
![]() измеримо по Лебегу.
измеримо по Лебегу.
Движения системы ![]() с начальным условием
с начальным условием ![]() реализуем с помощью ломаных Эйлера
реализуем с помощью ломаных Эйлера
![\begin{displaymath}
\begin{array}{c}
z_{\omega }(t)=z_{\omega }(t_{i})-(t-t_{i})...
...{\omega }(t_{i})),\\ [2ex]
t_{i}\leq t\leq t_{i+1},
\end{array}\end{displaymath}](img156.gif) |
(3.4) |
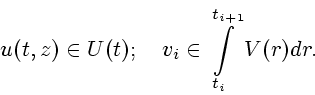 |
(3.5) |
На отрезке
![]() ломаные
ломаные ![]() удовлетворяют
условиям теоремы Арцела
удовлетворяют
условиям теоремы Арцела ![]() . Следовательно, на отрезке
. Следовательно, на отрезке
![]() определена функция
определена функция ![]() , которая
является равномерным пределом подпоследовательности ломаных
при диаметре разбиения
, которая
является равномерным пределом подпоследовательности ломаных
при диаметре разбиения
![]() . Такую
функцию будем называть движением, порожденным управлением
. Такую
функцию будем называть движением, порожденным управлением
![]() .
.
Считаем, что при ![]() построен стабильный мост, удовлетворяющий условию стабильности
построен стабильный мост, удовлетворяющий условию стабильности
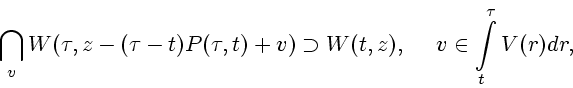 |
(3.6) |
| (3.7) |
Теорема 3.1. Для любой ломаной ![]() выполнено включение
выполнено включение
| (3.8) |
| (3.9) |
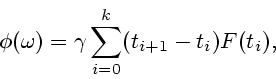
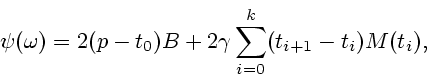
Д о к а з а т е л ь с т в о. Определим
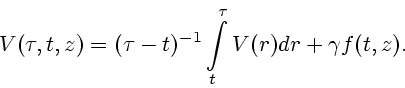 |
(3.10) |
Тогда включение ![]() примет следующий вид:
примет следующий вид:
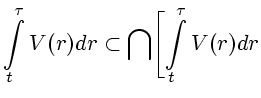 |
![$\displaystyle (\tau -t)\gamma \Bigl\{ f(t, z +\varepsilon \left[u_{1}-
u_{2}+s\right]) - f(t,z)\Bigr\} +$](img175.gif) |
||
![$\displaystyle + (\tau -t)A(\tau ,t,\varepsilon )S\Biggr].$](img176.gif) |
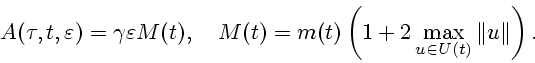 |
(3.11) |
Найдем функцию
![]() такую, чтобы выполнялось
условие стабильности
такую, чтобы выполнялось
условие стабильности ![]() для многозначной функции
для многозначной функции ![]() .
Из условия
.
Из условия ![]() следует, что включение
следует, что включение ![]() будет
выполнено, если
будет
выполнено, если
![]() .
Отсюда и из условия ограниченности
.
Отсюда и из условия ограниченности ![]() получим
получим
| (3.12) |
Подставив соотношения
Допустим, что функции ![]() и
и ![]() интегрируемы по Риману
на отрезке
интегрируемы по Риману
на отрезке
![]() .
Тогда при
.
Тогда при
![]() правая часть в
правая часть в ![]() стремится к следующей величине:
стремится к следующей величине:
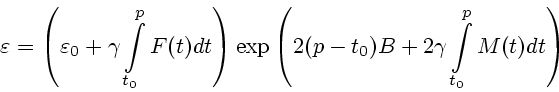
З а м е ч а н и е 3.1. В ряде случаев при построении стабильного
моста удобно брать
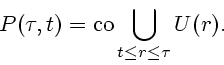
Рассмотрим задачу, в которой надо осуществить
включение ![]() , где
, где ![]() - замкнутое множество в
- замкнутое множество в ![]() .
Полагая
.
Полагая ![]() , ищем соотношение для моста в следующем виде:
, ищем соотношение для моста в следующем виде:
| (3.13) |
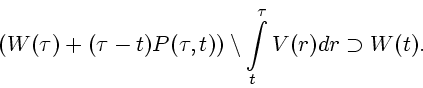
Для рассматриваемого случая алгоритм построения управления ![]() примет следующий вид:
примет следующий вид:
Поступила 10.10.99