5 Renormalization group method of Kohmoto-Kadanoff-Tang (KKT)

Being quasiperiodic structures of an intermediate state between the completely periodic crystals and the disordered amorphous solids, it is natural to associate them with quasicrystals. As is well known, the theoretical understanding of quasicrystals is based on the nonperiodic tiling of the plane due to Penrose. The one-dimensional version of these quasiperiodic structures, the Fibonacci lattices, was treated by Kohmoto, Kadanoff, and Tang in 1983 [8], and their method is called the ``KKT method." We are going to present this method applied to the analysis of the behavior of a particle subject to a potential $V(x), x \in {\Bbb R}.$

In quantum mechanics, this behavior is described by the one-dimensional Schrodinger equation (5.1)

$$\frac{{d^2 \Psi}}{{dx^2 }} + (E - V)\Psi = 0,$$ (5.1)

where $\Psi(x)$ is the wave function and $E$ is the total energy of the system. In this equation, $\Psi$ has no physical sense but it is the quantity $\vert\Psi\vert^2 dx$ that measures the probability of the particle being at point $x,$ or inside a box of amplitude $dx$ centered at $x.$

As is known, the mathematical normalization of the eigenfunctions

$$\int {\left\vert {\Psi (x)} \right\vert}^2 dx=1$$

admits a probabilistic interpretation: there is certainty of finding the particle in some point of the line.

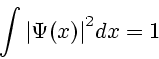
It is not possible to solve exactly equation (5.1), so the discretized version of it is the following

$$\Psi_{n + 1}-2\Psi_n + \Psi_{n - 1} =- (E - V_n)\Psi_n$$ (5.2)

where $\Psi_n$ denotes the wave function at the $n$th site and the potential $V_n$ takes two values $A$ and $B,$ arranged in the Fibonacci way:

$$S_0 =\{ B \};\quad S_1=\{ A \}; \ldots; \quad S_{j+1}=\{S_{j-1}, S_j\} \mbox{for} j \ge 1.$$

Equation (5.1) may be written as

$$\left( {\begin{array}{c} {\Psi _{n + 1} } \\ {\Psi _n } \... ...c} {\Psi _n } \\ {\Psi _{n - 1} } \\ \end{array}} \right),$$ (5.3)

where $M(n)$ is the ``transfer matrix"

$$M(n) = \left( {\begin{array}{cc} {-E + V_n+2 } & { - 1} \\ 1 & 0 \\ \end{array}} \right).$$ (5.4)

Successive applications of the transfer matrices give

$$\left( {\begin{array}{c} {\Psi _{N + 1} } \\ {\Psi _N } ... ...ray}{c} {\Psi _1 } \\ {\Psi _0 } \\ \end{array}} \right)$$

$$= \Omega (N)\left( {\begin{array}{*{20}c} {\Psi _1 } \\ {\Psi _0 } \\ \end{array}} \right) \\$$ (5.5)

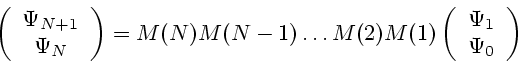
In order to get the energy spectrum, we look for solutions $\Psi_n$ that do not grow exponentially. Since each $\Psi(N)$ is a $2\times 2$ matrix with determinant equal to 1 (unimodular), the condition for $E$ to be in the spectrum i.e. to be an allowed energy is

$$\left\vert {\mbox{trace} \Omega (N)} \right\vert\le 2,$$

where the ``trace" of the matrix is the sum of the elements that appear in the main diagonal. Obviously, if this absolute value is greater than 2, the value of the energy is forbidden.

Summarizing, the KKT method applied to the study of the electronic properties of a one-dimensional quasicrystal is equivalent to calculating products of transfer matrices. The results indicate that the wave functions are either fractal or chaotic, and show a ``critical" behavior. The energy spectrum is a Cantor set with zero Lebesgue measure and the density of states at energy $E$ is concentrated with an index $\alpha_E$ (of the $\alpha - f(\alpha))$ multifractal Procaccia decomposition [9], which takes values in a range $[\alpha_E^{\min}, \alpha_E^{\max}].$ The fractal dimensions $f(\alpha_E)$ of these singularities in the Cantor set are also calculated, and the numerical values are all functions of powers of the Golden Mean $\phi!$

Let us quote some curious results about the continued fraction expansion of powers of the Golden Mean $\phi$

$$\begin{array}{l} \phi = \overline {\left[ 1 \right]}, \; \... ... {1,121} } \right], \; ........................... \end{array}$$

In general case, we prove that

$$\phi^{2n+1}=[\overline {L(2n+1)}],$$ (5.6)

$$\phi^{2n}=[L(2n)-1,\overline {1,L(2n)-2}],$$ (5.7)

where $L(n)$ are the Lucas numbers mentioned above. It is well known that Fibonacci numbers have the representation

$$F(n)=\frac{1}{\sqrt{5}}\left(\phi^{n+1}- \frac{(-1)^{n+1}}{\phi^{n+1}}\right).$$

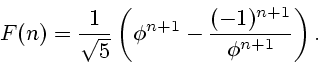
Also, it is easily to deduce by induction the following formula for Lucas numbers [31]:

$$L(n)=\phi^n+ \frac{(-1)^{n}}{\phi^{n}}.$$ (5.8)

Indeed, we have

$$L(n+1)=L(n)+L(n-1)=\phi^n+\frac{(-1)^{n}}{\phi^{n}}+ \phi^{n-1}+ \frac{(-1)^{n-1}}{\phi^{n-1}}$$

$$= \phi^{n+1}+ \frac{(-1)^{n}}{\phi^{n}}(1-\phi)= \phi^{n+1}+\frac{(-1)^{n}}{\phi^{n}}\left(-\frac{1}{\phi}\right)$$

$$= \phi^{n+1}+\frac{(-1)^{n+1}}{\phi^{n+1}}.$$

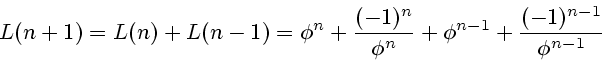
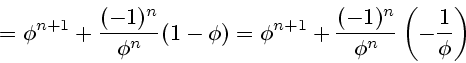
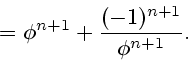
Now we obtain (5.6):

$$\phi^{2n+1}=L(2n+1)+\frac{1}{\phi^{2n+1}}=L(2n+1)+\frac{1} {\displaystyle L(2n+1)+ \frac{1}{\ddots}}=[\overline {L(2n+1)}].$$

Let us prove (5.7). Using (5.8) gives

$$(\phi^{2n})^2-L(2n)\phi^{2n}+ 1=0.$$

Setting $L'(2n)=L(2n)-2,$ we have

$$(\phi^{2n}-1)\phi^{2n}-(\phi^{2n}-1)=L'(2n)\phi^{2n},$$

$$\phi^{2n}-1=L'(2n)+\frac{1}{\displaystyle 1+ \frac{1}{\phi^{2n}-1}}= [\overline {L'(2n),1}],$$

$$\phi^{2n}=[L'(2n)+1,\overline {1,L'(2n)}]=[L(2n)-1,\overline {1,L(2n)-2}].$$

Thus, in the case of even powers, the continued fraction is periodic, being the first coefficient of the sum of the two forming the period, while in the case of uneven powers, the continued fraction is purely periodic. Let us add that this behavior is found only when integer powers of $\phi$ are considered. If instead we develop an irrational power of $\phi$ like

$$\phi^\phi = \left[ {2,5,1,1,1,1,10,1,1,2,8,7643,4,1,51,2,2,8,5,2, \ldots } \right],$$

no period is found.

This subject needs much more research: the question of explaining this fascinating behavior remains open.