4 Pisot and Salem numbers

Let us consider the set $U$ of real algebraic numbers greater than 1 whose remaining conjugates have a modulus at most equal to 1. This set is divided into two disjoint sets, $S$ and $T.$ The set $S$ of Pisot numbers (introduced by Charles Pisot, 1910-1984, in his famous thesis published in 1938) or else Pisot - Vijayaraghavan numbers (PV numbers), is the set of real algebraic numbers $\theta > 1$ whose other conjugates have a modulus strictly smaller than 1. The set $T$ of Salem numbers (discovered by Raphael Salem, 1898-1963) is the set of real algebraic numbers $\tau > 1$ whose other conjugates have a modulus at most equal to 1, one at least having a modulus equal to 1 [3].

The sets $S$ and $T$ define a partition of $U.$ All rational numbers greater than 1 belong to $S.$ The quadratic numbers in $S$ are zeros of second degree polynomials with integer coefficients. It is easy to prove that $S$ is a closed set on the real line. The set of limit points of $S$ is called the ``derived set of $S$" and is denoted by $S'.$ Furthermore, if $\theta$ is a PV number, then $\theta^m\in S'$ for every integer $m\ge 2.$ This implies that all PV numbers of degree $2\in S',$ the Golden Mean being the smallest of them and also the least element of $S'.$

Quite recently, it has been discovered ([4], [5], [6]) that PV numbers are natural candidates for coordinating quasicrystalline nodes in 1, 2 or 3 dimensions, and also the Bragg peaks in related diffraction patterns. In the observed cases, the following Pisot numbers appear as self-similarity ratios in quasicrystalline structures:

$$\begin{array}{l} x^2 - x - 1 = 0 \Rightarrow \phi = \frac{... ...- 4x + 1 = 0 \Rightarrow \delta = 2 + \sqrt 3 \\ \end{array}$$

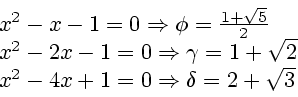
The first figure (the well-known Golden Mean) corresponds to penta- or decagonal quasilattices. The second one (the Silver Mean) corresponds to the octagonal case, and the third one, to the dodecagonal case. Certainly, the Metallic Means whose expansion in continued fractions is purely periodic are quadratic PV numbers because they are the positive solutions of quadratic equations of the form $x^2 - px - 1 = 0, p$ natural number.

In addition, the positive solutions of quadratic equations of the type $x^2-px+1=0,$ where $p \ge 3,$ are also quadratic PV numbers with purely periodic continued fraction expansions, where the condition that the terms of the continued fraction have to be positive has been relaxed [7]. For example,

$$x^2-3x+1=0 \Rightarrow x=3-\frac{1}{{3-\frac{1}{{3-\ddots}}}} = [{\overline{3 - }}].$$

(At the same time, $x=[2,\overline {1}]$.)

On the contrary, there are no examples of Salem numbers as simple as the ones given for PV numbers because there exist no Salem numbers of degree less than 4. Notwithstanding, both sets of PV numbers and of Salem numbers have many important applications not only in the quasicrystalline context, where they could play the same role as ordinary integers do in crystallography, but also in the formal study of power series and harmonic analysis.