This is the set of positive irrational numbers obtained by taking
![]()
![]()
![]()
![]() in equation (1.3) and considering
different values for the parameters
in equation (1.3) and considering
different values for the parameters ![]() and
and ![]() .
.
D e f i n i t i o n. The metallic means family (MMF) is the set of
positive eigenvalues of the matrix (1.6) for different
values of natural number ![]() and integer
and integer ![]() with
with ![]()
All the members of this family are positive quadratic irrational numbers that are the positive solutions of quadratic equation (1.4).
Let us begin with
![]() . Then it is very easy to
find the members of the MMF that satisfy this equation, expanding
them in continued fractions. In fact, if
. Then it is very easy to
find the members of the MMF that satisfy this equation, expanding
them in continued fractions. In fact, if ![]() then
then ![]() , which can be written
, which can be written
![]() . Replacing
iteratively the value of
. Replacing
iteratively the value of ![]() of the second term, we have
of the second term, we have
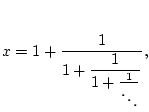 that is,
that is,
![]() , a purely periodic continued fraction that defines
the Golden Mean,
, a purely periodic continued fraction that defines
the Golden Mean,
Analogously, if ![]() and
and ![]() we obtain the Silver Mean:
we obtain the Silver Mean:
For
![]() , the metallic mean
, the metallic mean ![]() is
is
![]() a striking
result related to the continued fraction expansion of odd powers
of the Golden Mean. It is interesting to mention that odd powers
as well as even powers of the Golden Mean have interesting and
different continued fraction expansions in terms of Lucas numbers
a striking
result related to the continued fraction expansion of odd powers
of the Golden Mean. It is interesting to mention that odd powers
as well as even powers of the Golden Mean have interesting and
different continued fraction expansions in terms of Lucas numbers
![]() (
(
![]() , as for
, as for ![]() but
but
![]() )
[1]. The remaining metallic means are
)
[1]. The remaining metallic means are
![\begin{displaymath}
\sigma_p^1=[\overline{p}]=\frac{p+\sqrt{p^2+4}}{2},\;p=5,6,7,\ldots,
\end{displaymath}](img74.gif)
The Golden Mean ![]() is the most irrational of all irrational numbers.
is the most irrational of all irrational numbers.
If, instead, we consider equation
![\begin{displaymath}
\begin{array}{l}
\sigma_1^4=[2,\overline{1,1,3}];\quad\sigma...
...{1,5}];\quad \sigma_1^{12}=4=
[4,\overline 0 ] \\
\end{array}\end{displaymath}](img81.gif)
Precisely,
Indeed, we have
![]() , whence
, whence
![]() , which proves the first
assertion. The second is obvious. Let
, which proves the first
assertion. The second is obvious. Let ![]() . Then set
. Then set
![]() From (2.4) we obtain
From (2.4) we obtain
![]() and
and
![]()
![]()
![]() Finally, let
Finally, let ![]() . Then set again
. Then set again
![]() and
obtain
and
obtain
![]() and
and
![]()
![$y= 1+\frac{1}{(2n-1)y}=
1+\frac{1}{\displaystyle 2n-1+\frac{1}{\displaystyle y}} =
[\overline {1,2n-1}],$](img99.gif)
![]()