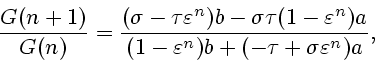A Fibonacci sequence is a sequence of integers where every number
is the sum of the two previous ones. Such sequences are called
``secondary Fibonacci sequences" to distinguish them from
the tertiary Fibonacci sequences, where every term is the sum of
the three previous terms. Beginning with
![]() we get
we get
The following assertion holds:
If the limit
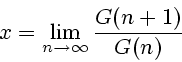
Indeed, from (1.3) we get
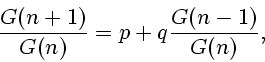
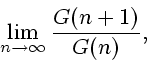
Proof. To find an expression for the ![]() th term of the GSFS,
let us write a matrix equation equivalent to (1.3)
th term of the GSFS,
let us write a matrix equation equivalent to (1.3)
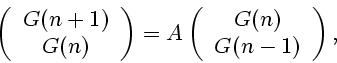
It is easily seen that
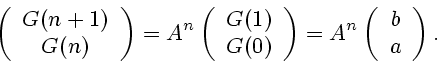
Thus, the problem is reduced to finding the ![]() th power of the
matrix
th power of the
matrix ![]() . The characteristic equation of
. The characteristic equation of ![]() is
is
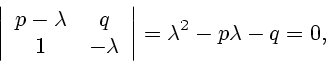
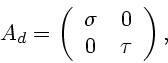
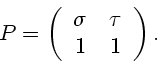
Set
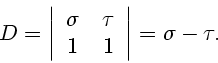
It is easy to check that
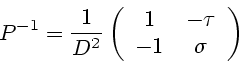
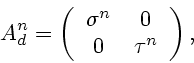
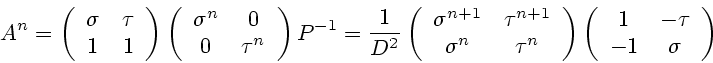
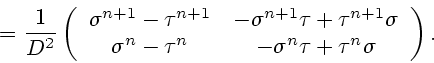
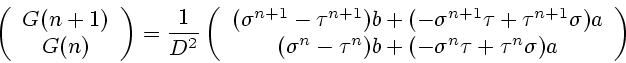
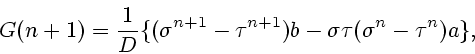
It follows that
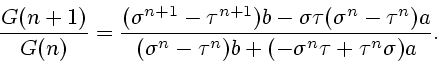
Setting
![]() and taking into account that
and taking into account that
![]() , we obtain
, we obtain