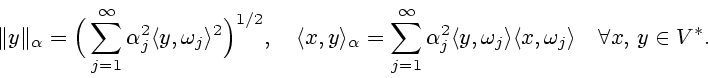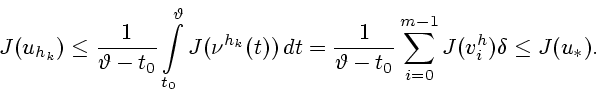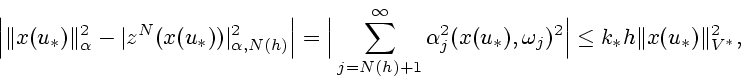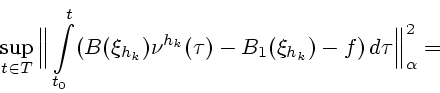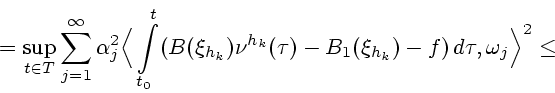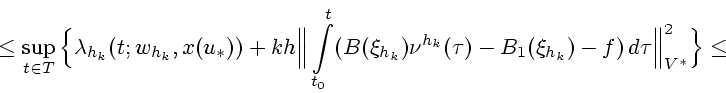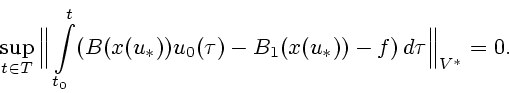

Next: 3 Пример
Up: MAKSIMOV
Previous: 1 Постановка задачи
Перейдем к описанию алгоритма решения задачи.
Рассмотрим две последовательности:
таких, что множество линейных комбинаций 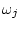 плотно в
плотно в 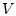 .
Пусть номер
.
Пусть номер 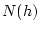 таков, что
таков, что
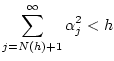 .
Введем искусственное время
.
Введем искусственное время
![$t\in T=[t_0,\vartheta ]$](img52.gif) ,
,
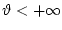 .
На промежутке
.
На промежутке 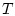 выберем семейство равномерных сеток
выберем семейство равномерных сеток
с диаметрами 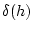 .
Рассмотрим вспомогательную управляемую систему, описываемую
конечномерной системой обыкновенных дифференциальных уравнений
.
Рассмотрим вспомогательную управляемую систему, описываемую
конечномерной системой обыкновенных дифференциальных уравнений
с управлением 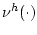 . Фазовую траекторию системы обозначим
. Фазовую траекторию системы обозначим
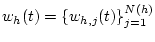 ,
, 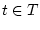 .
Управлять моделью будем по принципу обратной связи,
разбив весь процесс на
.
Управлять моделью будем по принципу обратной связи,
разбив весь процесс на 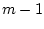 однотипных шагов.
В течение
однотипных шагов.
В течение 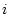 -го шага, осуществляемого на отрезке времени
-го шага, осуществляемого на отрезке времени
![$[\tau_i,\tau_{i+1}]$](img63.gif) , выполним следующие операции.
Сначала, в момент
, выполним следующие операции.
Сначала, в момент 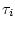 ,
,  , вычислим управление
, вычислим управление
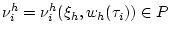 :
:
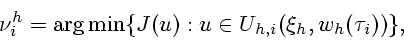 |
(5) |
где
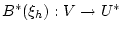 - оператор, сопряженный к оператору
- оператор, сопряженный к оператору
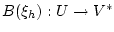 ,
символ
,
символ
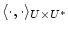 означает двойственность
между пространствами
означает двойственность
между пространствами 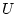 и
и 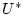 .
После этого, действуя на модель в течение промежутка времени
.
После этого, действуя на модель в течение промежутка времени
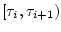 постоянным управлением
постоянным управлением
переведем фазовую траекторию из состояния
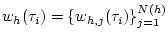 в состояние
в состояние
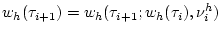 .
Процедуру закончим в момент
.
Процедуру закончим в момент 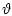 .
.
Заметим, что
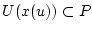 , множество всех
, множество всех
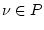 , порождающих решение
, порождающих решение 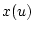 ,
выпукло, ограничено и замкнуто.
Пусть
,
выпукло, ограничено и замкнуто.
Пусть
Будем говорить [11], что 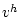 сходится к
сходится к 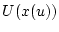 слабо, если
предел любой слабо сходящейся последовательности
слабо, если
предел любой слабо сходящейся последовательности
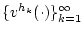 ,
(
,
(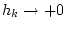 при
при 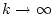 )
принадлежит
)
принадлежит 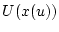 . (Так как
. (Так как 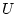 - рефлексивно, то такие
последовательности существуют).
- рефлексивно, то такие
последовательности существуют).
Теорема 2.1. Пусть
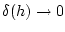 при
при 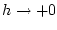 .
Тогда
.
Тогда
Если функционал 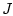 строго выпуклый, то
строго выпуклый, то 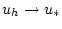 в
в 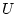 .
.
Прежде, чем переходить к доказательству теоремы, приведем
одно вспомогательное утверждение.
Обозначим
Лемма 2.1. Справедливы неравенства
Здесь
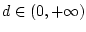 - постоянная, выписываемая в явном виде и
не зависящая от
- постоянная, выписываемая в явном виде и
не зависящая от 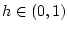 ,
, 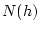 ,
, 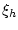 ,
,
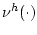 и
и 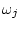 .
.
Д о к а з а т е л ь с т в о. Для доказательства леммы оценим изменение величины 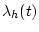 при
при
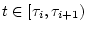 .
Имеем
.
Имеем
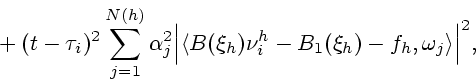 |
(6) |
где
В силу условия 1.1.2 и неравенств (2)
![\begin{displaymath}% -----------------------------------------------------------...
...,d\tau\le k_1, \quad
t\in T,\quad j\in [1,\ldots,N(h)],
%(7)
\end{displaymath}](img106.gif) |
(7) |
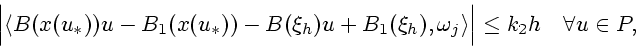 |
(8) |
Далее имеем
Отсюда и из (8) выводим
Значит,
Поэтому
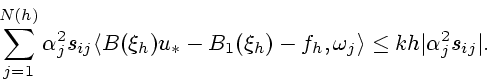 |
(9) |
Тогда в силу правила выбора 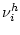 (см. (5)) и
(9) имеем
(см. (5)) и
(9) имеем
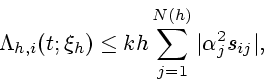 |
(10) |
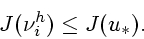 |
(11) |
Кроме того,
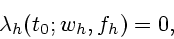 |
(12) |
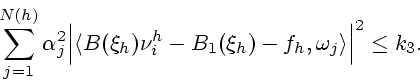 |
(13) |
Заметим, что в оценках (7)-(13) постоянные 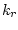 ,
,
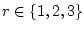 не зависят от
не зависят от 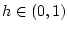 ,
, 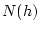 ,
, 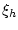 ,
, 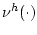 и
и 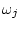 .
Из (6), (10), (13) следует при
.
Из (6), (10), (13) следует при
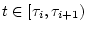 неравенство
неравенство
Значит
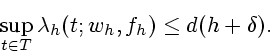 |
(14) |
Справедливость леммы следует из (11), (14). Лемма доказана.
Д о к а з а т е л ь с т в о т е о р е м ы 2.1. Предполагая противное, заключаем, что
найдется слабо сходящаяся последовательность
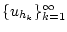 такая, что
такая, что
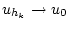 слабо в
слабо в 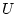 , но
, но
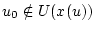 .
Символами
.
Символами
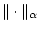 и
и
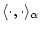 обозначим
обозначим 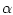 -норму
в пространстве
-норму
в пространстве 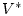 и отвечающее ей скалярное произведение
и отвечающее ей скалярное произведение
Заметим, что на ограниченных множествах сходимость в 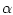 -норме
эквивалентна слабой сходимости.
-норме
эквивалентна слабой сходимости.
Пусть
![$U_x^0[\gamma]$](img131.gif) (
(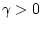 ) - множество всех элементов
) - множество всех элементов 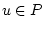 таких, что
таких, что
Здесь величина 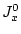 определена согласно (3).
В силу выпуклости функционала
определена согласно (3).
В силу выпуклости функционала 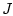
Нетрудно видеть, что справедливо неравенство
где 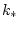 не зависит от
не зависит от 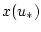 . Отсюда и из леммы 1 выводим
. Отсюда и из леммы 1 выводим
т. е.
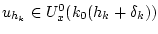 .
Учитывая условие 1.1.2 и неравенства (2), из последнего неравенства
получаем
.
Учитывая условие 1.1.2 и неравенства (2), из последнего неравенства
получаем
Отсюда и следует справедливость теоремы.


Next: 3 Пример
Up: MAKSIMOV
Previous: 1 Постановка задачи
2003-05-08
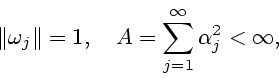
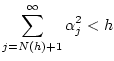 .
Введем искусственное время
.
Введем искусственное время
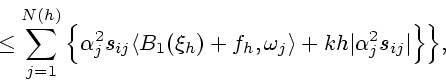
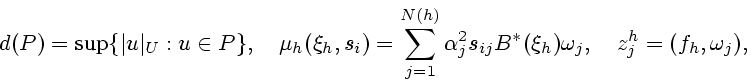
![]() , множество всех
, множество всех
![]() , порождающих решение
, порождающих решение ![]() ,
выпукло, ограничено и замкнуто.
Пусть
,
выпукло, ограничено и замкнуто.
Пусть
![]() при
при ![]() .
Тогда
.
Тогда
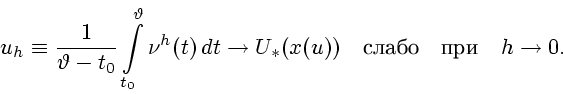
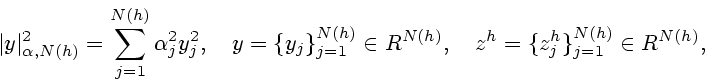
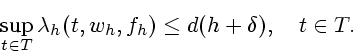
![]() при
при
![]() .
Имеем
.
Имеем
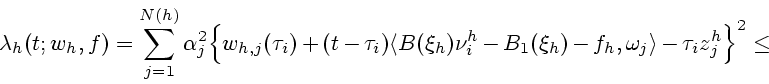
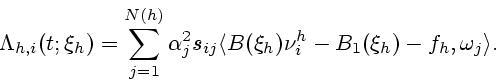
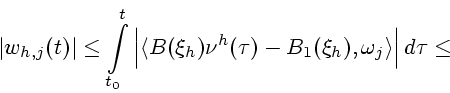
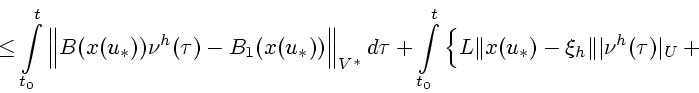
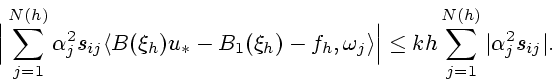
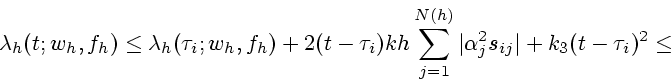
![]() такая, что
такая, что
![]() слабо в
слабо в ![]() , но
, но
![]() .
Символами
.
Символами
![]() и
и
![]() обозначим
обозначим ![]() -норму
в пространстве
-норму
в пространстве ![]() и отвечающее ей скалярное произведение
и отвечающее ей скалярное произведение