

Next: 2 Алгоритм решения
Up: MAKSIMOV
Previous: MAKSIMOV
Пусть
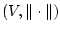 - сепарабельное и рефлексивное банахово
пространство,
- сепарабельное и рефлексивное банахово
пространство,
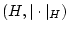 - гильбертово пространство,
отождествляемое с его сопряженным:
- гильбертово пространство,
отождествляемое с его сопряженным: 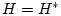 .
Предполагается, что
.
Предполагается, что 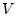 вложено в
вложено в 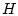 плотно и непрерывно.
Заданы равномерно выпуклое банахово пространство
плотно и непрерывно.
Заданы равномерно выпуклое банахово пространство
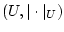 , выпуклое ограниченное и замкнутое множество
, выпуклое ограниченное и замкнутое множество 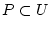 ,
а также семейство операторов
,
а также семейство операторов 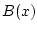 , удовлетворяющих условию:
, удовлетворяющих условию:
Условие 1.1.
1) Oтображение
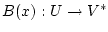 линейно
линейно
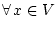 ;
;
2)
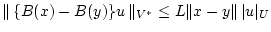
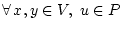 ;
; 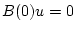 ;
;
3)
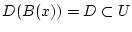
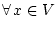 ,
,
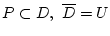 .
.
Здесь 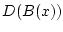 - область определения оператора
- область определения оператора
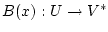 ,
символ
,
символ 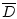 означает замыкание множества
означает замыкание множества 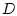 в норме пространства
в норме пространства 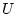 .
Пусть также задан оператор
.
Пусть также задан оператор
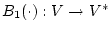 со свойствами:
со свойствами:
Рассмотрим операторное уравнение
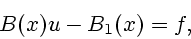 |
(1) |
где 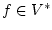 - фиксированный элемент.
Обсуждаемая задача состоит в следующем.
Параметр
- фиксированный элемент.
Обсуждаемая задача состоит в следующем.
Параметр 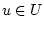 , а также элемент
, а также элемент 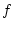 неизвестны.
Известен параметр
неизвестны.
Известен параметр 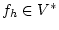 - приближение
- приближение 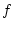 :
:
Кроме того, известно, что 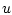 принадлежит множеству
принадлежит множеству
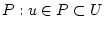 .
Требуется указать алгоритм, позволяющий по неточным измерениям решения
.
Требуется указать алгоритм, позволяющий по неточным измерениям решения
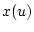 уравнения (1) и правой части
уравнения (1) и правой части 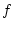 вычислить (приближенно)
параметр
вычислить (приближенно)
параметр 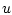 .
Результат измерения
.
Результат измерения 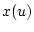 - величина
- величина 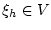 -
удовлетворяет неравенству
-
удовлетворяет неравенству
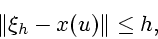 |
(2) |
где 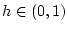 - параметр точности измерения.
В дальнейшем предполагается, что неизвестному параметру
- параметр точности измерения.
В дальнейшем предполагается, что неизвестному параметру 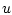 отвечает единственное
решение
отвечает единственное
решение 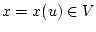 уравнения (1), т. е. единственный
элемент
уравнения (1), т. е. единственный
элемент 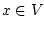 такой, что
такой, что
Здесь символ
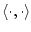 означает двойственность между
пространствами
означает двойственность между
пространствами 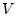 и
и 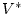 .
Сам же элемент
.
Сам же элемент 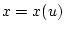 может порождаться различными реализациями
параметра
может порождаться различными реализациями
параметра 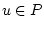 . Именно, множество
. Именно, множество
может быть не одноэлементным.
В этом случае будем предполагать, что нас интересуют не все параметры
из этого множества, а лишь некоторые - те, которые выделены с помощью
того или иного принципа выбора.
В теории некорректных задач за принцип выбора часто принимается
принцип минимума некоторого функционала.
Следуя этому подходу, будем считать, что на множестве 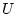 определен
функционал
определен
функционал 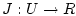 .
.
Итак, обсуждаемая задача состоит в построении алгоритма приближенного
вычисления экстремального значения
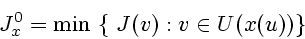 |
(3) |
и экстремального входа
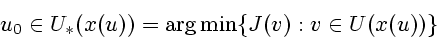 |
(4) |
по измерению с ошибкой решения уравнения (1) 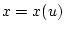 и неточно известной правой части
и неточно известной правой части 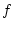 .
.
В дальнейшем полагаем, что 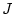 - выпуклый собственный
слабо полунепрерывный снизу функционал.
В этом случае задача (3), (4) имеет решение, ибо,
как легко видеть, множество
- выпуклый собственный
слабо полунепрерывный снизу функционал.
В этом случае задача (3), (4) имеет решение, ибо,
как легко видеть, множество 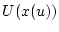 выпукло, ограничено и замкнуто.
выпукло, ограничено и замкнуто.
Рассматриваемая задача по своей сути является стационарной.
Для ее решения, однако, предлагается регуляризованный динамический алгоритм.
Алгоритм является пошаговым: он работает на фиксированном временном промежутке.
В основу построения предлагаемого алгоритма положена идея стабилизации
(удержания движения вблизи нуля) с помощью подходящей скалярной функции
Ляпунова. Процесс стабилизации этой функции (выбора управления в модели)
осуществляется по закону обратной связи и опирается на принцип
экстремального сдвига Н. Н. Красовского в сочетании с методом невязки.


Next: 2 Алгоритм решения
Up: MAKSIMOV
Previous: MAKSIMOV
2003-05-08
![]() линейно
линейно
![]() ;
; ![]()
![]() ;
; ![]() ;
;
![]()
![]() ,
,
![]() .
.
![]() - область определения оператора
- область определения оператора
![]() ,
символ
,
символ ![]() означает замыкание множества
означает замыкание множества ![]() в норме пространства
в норме пространства ![]() .
Пусть также задан оператор
.
Пусть также задан оператор
![]() со свойствами:
со свойствами:
![]() - выпуклый собственный
слабо полунепрерывный снизу функционал.
В этом случае задача (3), (4) имеет решение, ибо,
как легко видеть, множество
- выпуклый собственный
слабо полунепрерывный снизу функционал.
В этом случае задача (3), (4) имеет решение, ибо,
как легко видеть, множество ![]() выпукло, ограничено и замкнуто.
выпукло, ограничено и замкнуто.