| (15) |
Рассмотрим нелинейное эллиптическое уравнение
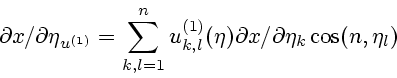
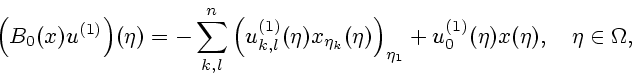
Положим
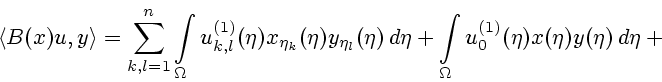
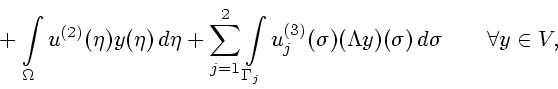
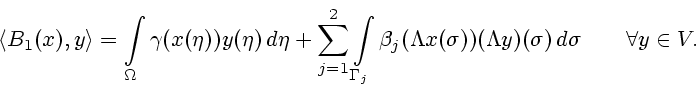
Под решением уравнения (15), отвечающим элементу
![]() ,
будем понимать элемент
,
будем понимать элемент ![]() , удовлетворяющий соотношению
, удовлетворяющий соотношению
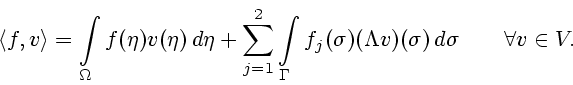
Задача восстановления коэффициентов ![]() эллиптического оператора
эллиптического оператора
![]() , распределенного управления
, распределенного управления ![]() и граничных управлений
и граничных управлений
![]() ,
, ![]() , по неточным измерениям решения
, по неточным измерениям решения ![]() уравнения (15) может быть рассмотрена как частный случай описанной выше
задачи. Это следует из приведенного ниже утверждения 3.1.
уравнения (15) может быть рассмотрена как частный случай описанной выше
задачи. Это следует из приведенного ниже утверждения 3.1.
Действительно, пусть
![]() ,
,
![]() ,
,
![]() - выпуклое, ограниченное
и замкнутое множество в
- выпуклое, ограниченное
и замкнутое множество в
![]() ,
,
![]() - гильбертово пространство такое, что
- гильбертово пространство такое, что
Утверждение 3.1 [14]. Выражение
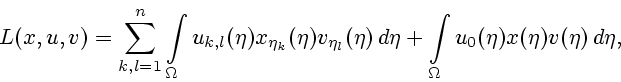
Поступила 16.07.99