| (1.1) |
Рассмотрим линейную управляемую систему
Введем дискретные аналоги квазистратегий первого игрока (см. [4]).
Пусть
![]() - разбиение отрезка
- разбиение отрезка
![]() (
(
![]() )
и
)
и ![]() - (малый) положительный параметр. Далее
- (малый) положительный параметр. Далее
![]() .
Фиксируем конечное семейство точек из
.
Фиксируем конечное семейство точек из ![]() таких, что их выпуклая
оболочка
таких, что их выпуклая
оболочка ![]() отклоняется от
отклоняется от ![]() не более, чем на
не более, чем на ![]() в метрике Хаусдорфа. Также фиксируем
конечное семейство точек из
в метрике Хаусдорфа. Также фиксируем
конечное семейство точек из ![]() таких, что их выпуклая оболочка
отклоняется от
таких, что их выпуклая оболочка
отклоняется от ![]() не более, чем на
не более, чем на ![]() в метрике Хаусдорфа;
множество всех точек указанного семейства обозначим
в метрике Хаусдорфа;
множество всех точек указанного семейства обозначим ![]() .
Всякую функцию
.
Всякую функцию
![]() ,
постоянную на каждом полуинтервале
,
постоянную на каждом полуинтервале
![]() (
(
![]() ), будем называть
), будем называть
![]() -управлением первого игрока и отождествлять
с вектором
-управлением первого игрока и отождествлять
с вектором
![]() ,
где
,
где
![]() (
(![]() ). Таким образом, множество
всех
). Таким образом, множество
всех
![]() -управлений первого игрока есть
-управлений первого игрока есть
![]() ;
далее будем его также обозначать как
;
далее будем его также обозначать как
![]() . Всякую
функцию
. Всякую
функцию
![]() ,
постоянную на каждом полуинтервале
,
постоянную на каждом полуинтервале
![]() (
(
![]() ), будем называть
), будем называть
![]() -управлением второго игрока и отождествлять
с вектором
-управлением второго игрока и отождествлять
с вектором
![]() , где
, где
![]() (
(![]() ; таким образом, множество всех
; таким образом, множество всех
![]() -управлений второго игрока есть
-управлений второго игрока есть
![]() ;
далее будем для него также использовать обозначение
;
далее будем для него также использовать обозначение
![]() .
.
З а м е ч а н и е 1. Множество
![]() конечно.
конечно.
Движение, порождаемое
![]() -управлением
-управлением ![]() первого
игрока и
первого
игрока и
![]() -управлением
-управлением ![]() второго игрока,
определим как решение
второго игрока,
определим как решение ![]() дифференциального уравнения (1.1)
c
дифференциального уравнения (1.1)
c ![]() ,
, ![]() для
для
![]() (
(![]() )
и с начальным условием
)
и с начальным условием ![]() ; конечную точку
; конечную точку ![]() этого решения обозначим через
этого решения обозначим через ![]() . Заметим, что
. Заметим, что
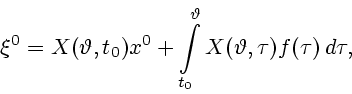
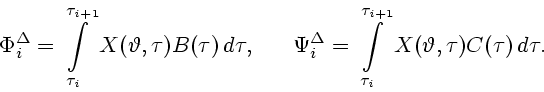
Отображение ![]() множества
множества
![]() всех
всех
![]() -управлений второго
-управлений второго
игрока в множество
![]() всех
всех
![]() -управлений первого игрока будем называть
-управлений первого игрока будем называть
![]() -квазистратегией первого игрока, если
оно удовлетворяет следующему условию неупреждаемости:
для любых
-квазистратегией первого игрока, если
оно удовлетворяет следующему условию неупреждаемости:
для любых
![]() ,
, ![]() ,
,
![]() таких, что
таких, что ![]() при всех
при всех ![]() , выполняется
, выполняется
![]() при всех
при всех ![]() . Будем говорить, что
. Будем говорить, что
![]() -квазистратегия
-квазистратегия ![]() первого игрока
первого игрока ![]() -наводящая, если
-наводящая, если
![]() для любого
для любого
![]() .
.
(i) если существует ![]() -наводящая позиционная стратегия первого
-наводящая позиционная стратегия первого
игрока, то существует
![]() -наводящая
-наводящая
![]() -квазистратегия первого игрока,
-квазистратегия первого игрока,
(ii) если существует ![]() -наводящая
-наводящая
![]() -квазистратегия
первого игрока, то существует
-квазистратегия
первого игрока, то существует
![]() -наводящая
позиционная стратегия первого игрока.
-наводящая
позиционная стратегия первого игрока.
З а м е ч а н и е 2. Числа ![]() и
и ![]() могут быть выражены явно через модули
непрерывности матриц-функций
могут быть выражены явно через модули
непрерывности матриц-функций
![]() ,
,
![]() ,
,
![]() ,
константы, равномерно ограничивающие нормы их значений, и константы,
равномерно ограничивающие нормы элементов из множеств
,
константы, равномерно ограничивающие нормы их значений, и константы,
равномерно ограничивающие нормы элементов из множеств ![]() и
и ![]() .
.
Доказательство леммы 1 опускаем.
Пусть
![]() - точная нижняя грань всех
- точная нижняя грань всех
![]() , для которых существует
, для которых существует ![]() -наводящая
-наводящая
![]() -квазистратегия первого игрока. Из леммы 1 легко получается
-квазистратегия первого игрока. Из леммы 1 легко получается
З а м е ч а н и е 3. Согласно замечанию ![]() , числа
, числа ![]() и
и ![]() могут быть выписаны
явно.
могут быть выписаны
явно.
Итак, при достаточно малых
![]() и
и ![]() задача об
аппроксимации цены
задача об
аппроксимации цены ![]() сводится к задаче о нахождении величины
сводится к задаче о нахождении величины
![]() . Последняя задача, в свою очередь,
может быть представлена как задача конечномерного выпуклого
программирования. Опишем это представление. Пусть
. Последняя задача, в свою очередь,
может быть представлена как задача конечномерного выпуклого
программирования. Опишем это представление. Пусть
![]() -
линейное пространство всех функций
-
линейное пространство всех функций
![]() (напомним, что
(напомним, что ![]() - размерность управляющего воздействия
первого игрока).
Вследствие конечности множества
- размерность управляющего воздействия
первого игрока).
Вследствие конечности множества
![]() пространство
пространство
![]() конечномерно. Превратим
конечномерно. Превратим
![]() в
евклидово пространство, вводя для каждых
в
евклидово пространство, вводя для каждых ![]() ,
,
![]() их скалярное произведение по формуле
их скалярное произведение по формуле
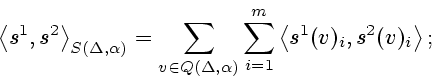
Пространство
![]() будем далее считать евклидовым;
скалярное произведение элементов
будем далее считать евклидовым;
скалярное произведение элементов ![]() ,
,
![]() зададим по формуле
зададим по формуле
Задача (1.7), (1.3), (1.4) есть,
очевидно, задача конечномерного выпуклого программирования.
Для решения этой задачи, в принципе, применимы стандартные
итерационные методы оптимизации. Однако, негладкость минимизируемой
функции, возникающая за счет входящей в нее операции максимизации
(см. (1.7)), и большая, вообще говоря, размерность задачи
создают серьезные трудности на пути конструктивной реализации
стандартных методов. Наша цель - указать конструктивный,
по возможности готовый для программирования, специализированный
алгоритм, позволяющий проверить неравенство
![]() при заданном
при заданном ![]() .
.
От задачи (1.7), (1.3), (1.4) перейдем
к задаче на минимум
Имея в виду этот факт, сосредоточимся на методе решения задачи (1.8), (1.3), (1.4).