2 Метод решения

За основу примем описанный в [7] итерационный метод решения оптимизационной задачи

$$J(z)\to\min,$$ (2.1)

$$z\in Z,$$ (2.2)

$$Fz=0.$$ (2.3)

Здесь $Z$ - выпуклый компакт в ${R}^{k_1}$, $J(\cdot)$ - выпуклая функция на $Z$, $F$ - линейный оператор из ${R}^{k_1}$ в ${R}^{k_2}$. Ниже через $\mathop{\rm Argmin}\nolimits \{ g(y): y\in Y\}$ обозначается множество всех точек минимума функции $g: Y\longmapsto {R}^1$.

Теорема 1   [7, теорема 8.2]. Пусть задача (2.1)-(2.3) имеет решение.
Пусть

$$t_0=0,\quad \lim_{k\to\infty} t_k=\infty,$$ (2.4)

$$\delta_k=t_{k+1}-t_k>0,\quad \mu_k=\sum_{i=0}^{k-1} \delta_i^2,\quad (k=0,1,\ldots),$$ (2.5)

$$\lim_{k\to\infty} \frac{\mu_k}{t_k}=0$$ (2.6)

и последовательности $(y^k)_{k=0}^{\infty}$ и $(\zeta^k)_{k=0}^{\infty}$ из ${R}^{k_1}$ заданы условиями

$$y^0=0,\quad y^{k+1}=y^k+\zeta^k\delta_k,$$ (2.7)

$$\zeta^k\in\mathop{\rm Argmin}\nolimits \left\{ \left< Fy^k,F\zeta\right>+\beta J(\zeta): \zeta\in Z\right\},$$

где $\beta$ - положительный параметр. Тогда последовательность
$(y^k/t^k)_{k=1}^{\infty}$ сходится к множеству $Z^0$ всех решений задачи (2.1)-(2.3)
$(\lim\limits_{k\to\infty} \mathop{\rm dist}\nolimits (y^k/t^k, Z^0)=0)$, а последовательность $\left( J(y^k/t^k) \right)_{k=1}^{\infty}$ сходится к оптимальному значению $J^0$ задачи (2.1)-(2.3). При этом существуют $K_1$, $K_2>0$ такие, что для всех $k=1, 2,\ldots$

$$\left\vert F\frac{y^k}{t^k} \right\vert^2\le K_1\frac{1}{t_k... ...ad J\left(\frac{y^k}{t_k}\right)\le J^0+ K_2\frac{\mu_k}{t_k}.$$

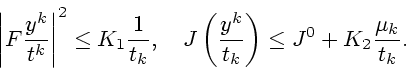
З а м е ч а н и е 4. Условия (2.4), (2.5) выполняются, например, при $\delta_k=1/k$ $(k=1,2,\ldots)$.

Переходя от $y^k$ (2.7) к $z^k=y^k/t^k$, заметим, что

$$z^1\in\mathop{\rm Argmin}\nolimits \left\{ J(z): z\in Z \right\},\quad z^{k+1}=(1-\nu_k)z^k+\nu_k \zeta^k,$$ (2.8)

$$\zeta^k\in \mathop{\rm Argmin}\nolimits \left\{ \left< Fz^k,F\zeta\right>+\beta_k J(\zeta): \zeta\in Z \right\},$$ (2.9)

где

$$\nu_k=\frac{\delta_k}{t_k+\delta_k},\quad \beta_k=\frac{\beta}{t_k}\quad (k=1,2,\dots).$$ (2.10)

Перефразируем теорему 1:

Теорема 2   Пусть задача (2.1)-(2.3) имеет решение, $\beta>0$, выполняются условия (2.4)-(2.6), (2.10), и последовательности $(z^k)_{k=1}^{\infty}$ и $(\zeta^k)_{k=1}^{\infty}$ из ${R}^{k_1}$ заданы условиями (2.8) и (2.9). Тогда

$$\lim_{k\to\infty} \mathop{\rm dist}\nolimits (z^k,Z^0)=0,\quad \lim_{k\to\infty} J(z^k)=J^0,$$

где $Z^0$ и $J^0$ - множество всех решений и оптимальное значение задачи (1.8)-(2.2) соответственно. При этом существуют $K_1$, $K_2>0$ такие, что при всех $k=1, 2,\ldots$

$$\vert F z^k\vert^2\le K_1\frac{1}{t_k},\quad J(z^k)\le J^0+K_2\frac{\mu_k}{t_k}.$$

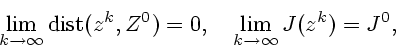
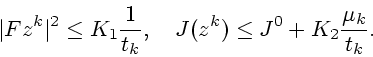
Задача (1.8), (1.3), (1.4) есть частный случай задачи (2.1)-(2.3); роль ограничений (2.2) и (2.3) играют, соответственно (1.3) и (1.4). Конкретизируем решающий алгоритм, описанный в теореме 2, для задачи (1.8), (1.3), (1.4). Фиксируем $\beta>0$ и зададим $t_k$, $\delta_k$, $\mu_k$, $\nu_k$, $\beta_k$ по (2.4)-(2.6), (2.10). Последовательности $(z^k)$ и $(\zeta^k)$ (2.8), (2.9), обозначаемые применительно к задаче (1.8), (1.3), (1.4) как $(s^k)$ и $(\sigma^k)$, суть последовательности из $S(\Delta,\alpha)$ такие, что

$$s^1\in\mathop{\rm Argmin}\nolimits \left\{ \sum_{v\in Q(\Del... ...a)} \mathop{\rm dist}\nolimits (x(s(v),v),M^{\gamma}): \right.$$ (2.11)

$$\left. \vphantom{\sum_{v\in Q(\Delta,\alpha)}} s(v)\in P(\Delta,\alpha)\quad (v\in Q(\Delta,\alpha)) \right\},$$

$$s^{k+1}=(1-\nu_k)s^k+\nu_k\sigma^k,$$ (2.12)

$$\sigma^k\in\mathop{\rm Argmin}\nolimits \{ \left< F_{\Delta,... ...\alpha)} \mathop{\rm dist}\nolimits (x(\eta(v),v),M^{\gamma}):$$ (2.13)

$$\eta(v)\in P(\Delta,\alpha)\quad (v\in Q(\Delta,\alpha))\}.$$

Преобразуем (2.11) и (2.13). Условие (2.11), очевидно, эквивалентно следующему семейству независимых условий:

$$s^1(v)\in \mathop{\rm Argmin}\nolimits \left\{ \mathop{\rm d... ...): u\in P(\Delta,\alpha)\right\}\quad (v\in Q(\Delta,\alpha));$$ (2.14)

$$\mathop{\rm dist}\nolimits (x(u,v),M^{\gamma})= \mathop{\rm ... ...i_i^{\Delta}u_i+\Psi_i^{\Delta}v_i\right),M^{\gamma}\right)={}$$

$${}=\max_{l\in L} \left[\left< l,\xi^0+\sum_{i=1}^m \left(\Ph... ...t>-\left(\rho^+(l\vert M)+ \gamma{\vert l\vert}\right)\right];$$ (2.15)

здесь и далее $\vert\cdot\vert$ - евклидова норма, $L$ - единичный шар в ${R}^n$, $\rho^+(\cdot\vert M)$ - опорная функция множества $M$ (тогда $l\longmapsto \rho^+(\cdot\vert M)+\gamma{\vert l\vert}$ - опорная функция $M^{\gamma}$). Пусть для $l\in {R}^n$

$$\rho^-(l\vert P_{\alpha})=\min_{u\in P_{\alpha}} \left< l,u\right>,\quad (l\in {R}^n)$$

$$u_{\Delta,\alpha}(l)_i\in\mathop{\rm Argmin}\nolimits \left\{ \left< (\Phi_i^{\Delta})'l,u\right>: u\in P_{\alpha}\right\};$$ (2.16)

здесь и далее $'$ - знак транспонирования. Введем обозначение для минимума по всем $u\in P(\Delta,\alpha)$ выражения, записанного в (2.15) в квадратных скобках:

$$\kappa_{\gamma}(l,v\vert\Delta,\alpha)=\left< l,\xi^0+\sum_{... ...>+ \sum_{i=1}^m \rho^-((\Phi_i^{\Delta})'l\vert P_{\alpha})-{}$$

$${}- (\rho^+(l\vert M)+\gamma{\vert l\vert})\quad (l\in {R}^n, v\in Q(\Delta,\alpha)).$$ (2.17)

Положим

$$l_{\gamma}^0(v\vert\Delta,\alpha)\in\mathop{\rm Argmax}\noli... ...l,v\vert\Delta,\alpha): l\in L\}\quad (v\in Q(\Delta,\alpha)).$$ (2.18)

Из (2.14), (2.15) следует, что

$$s^1(v)_i=u_{\Delta,\alpha}(l_{\gamma}^0(v\vert\Delta,\alpha))_i\quad (i=1,\ldots,m,\ v\in Q(\Delta,\alpha)).$$ (2.19)

Итак, (2.19) есть реализация условия (2.11).

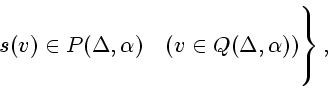
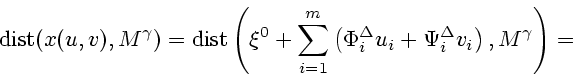
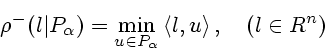
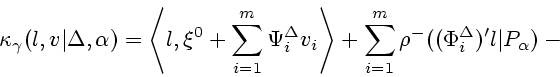
Рассмотрим условие (2.13). Согласно (1.5) и (1.6) имеем

$$\left< F_{\Delta,\alpha} s^k, F_{\Delta,\alpha}\eta\right>_{R(\Delta,\alpha)}={}$$

$${}= \sum_{v\in Q(\Delta,\alpha)} \sum_{w\in Q(\Delta,\alpha)... ...t)(v,w)_i, \left(F_{\Delta,\alpha}\eta\right)(v,w)_i\right>={}$$

$${}= \sum_{v\in Q(\Delta,\alpha)} \sum_{i=1}^m \sum_{w\in Q_i... ...)} \left< s^k(v)_i- s^k(w)_i,\quad \eta(v)_i-\eta(w)_i\right>,$$ (2.20)

где

$$Q_i(v\vert\Delta,\alpha)=\{ w\in Q(\Delta,\alpha): w_1=v_1,\ldots, w_i=v_i\}\quad (v\in Q(\Delta,\alpha)).$$ (2.21)

Вводя суммы

$$\lambda_i(s,v\vert\Delta,\alpha)=\sum_{w\in Q_i(v\vert\Delta,\alpha)} (s(v)_i-s(w)_i)$$ (2.22)

$$(i=1,\ldots,m,\ s\in S(\Delta,\alpha),\ v\in Q(\Delta,\alpha)),$$

запишем равенство (2.20) следующим образом:

$$\left< F_{\Delta,\alpha} s^k, F_{\Delta,\alpha} \eta\right>_{R(\Delta,\alpha)}= \omega_1-\omega_2,$$ (2.23)

где

$$\omega_1=\sum_{v\in Q(\Delta,\alpha)} \sum_{i=1}^m \left< \lambda_i(s^k,v\vert\Delta,\alpha),\eta(v)_i\right>,$$

$$\omega_2=\sum_{v\in Q(\Delta,\alpha)} \sum_{i=1}^m \sum_{w\i... ...t\Delta,\alpha)} \left< s^k(v)_i- s^k(w)_i,\eta(w)_i\right>={}$$

$${}= \sum_{w\in Q(\Delta,\alpha)} \sum_{i=1}^m \sum_{v\in Q_i... ...rt\Delta,\alpha)} \left< s^k(v)_i-s^k(w)_i,\eta(w)_i\right>={}$$

$${}= -\sum_{w\in Q(\Delta,\alpha)} \sum_{i=1}^m \left< \lambda_i(s^k,w\vert\Delta,\alpha),\eta_i(w)_i\right>=-\omega_1.$$

Мы видим, что правая часть (2.23) равна $2\omega_1$. Обращаясь к виду $\omega_1$, замечаем, что условие (2.13) эквивалентно следующему семейству независимых условий:

$$\sigma^k(v)\in\mathop{\rm Argmin}\nolimits \{ \sum_{i=1}^m \... ...\right>+\beta_k\mathop{\rm dist}\nolimits (x(u,v),M^{\gamma}):$$

$$u\in P(\Delta,\alpha)\}\quad (v\in Q(\Delta,\alpha)).$$ (2.24)

Теперь, учитывая равенство (2.15), с помощью обозначений (2.17), (2.18) и определения (2.16), так же, как при выводе (2.19), получаем следующую переформулировку (2.24):

$$\sigma^k(v)_i=u_{\Delta,\alpha}(\lambda_i(s^k,v\vert\Delta,\alpha)+ \beta_k l_{\gamma}^0(v\vert\Delta,\alpha))$$ (2.25)

$$(i=1,\ldots,m,\ v\in Q(\Delta,\alpha)).$$

Последнее есть реализация условия (2.13).

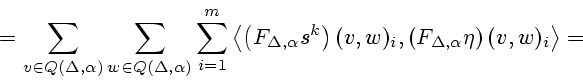
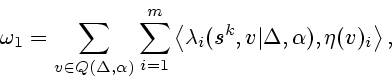
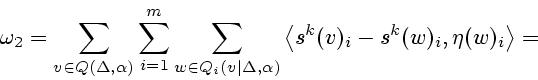
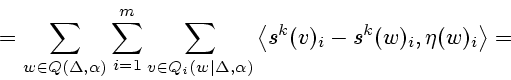
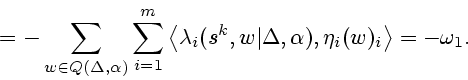
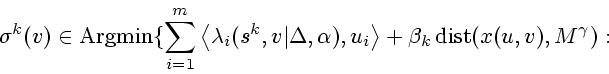
Итак, итерационный алгоритм (2.11)-(2.13) принимает вид (2.19),
(2.12), (2.25). Напомним, что данный алгоритм есть конкретизация для задачи (1.8), (1.3), (1.4) алгоритма, описанного в теореме 2. Таким образом, справедлива следующая

Теорема 3   Пусть $\beta>0$, выполняются условия (2.4)-(2.6), (2.10) и последовательности $(s^k)_{k=1}^{\infty}$ и $(\sigma^k)_{k=1}^{\infty}$ из $S(\Delta,\alpha)$ заданы согласно (2.19), (2.12), (2.25). Тогда

$$\lim_{k\to\infty}\mathop{\rm dist}\nolimits (s^k,S^0(\Delta,\alpha))=0,$$

$$\lim_{k\to\infty} \sum_{v\in Q(\Delta,\alpha)} \mathop{\rm dist}\nolimits (x(s^k(v),v), M^{\gamma})=I^0(\Delta,\alpha),$$

где $S^0(\Delta,\alpha)$ и $I^0(\Delta,\alpha)$ - соответственно множество всех решений и оптимальное значение задачи (1.8), (1.3), (1.4). При этом существуют $K_1$, $K_2>0$ такие, что при всех $k=1, 2,\ldots$

$$\vert F_{\Delta,\alpha} s^k\vert^2\le K_1\frac{1}{t_k},$$

$$\sum_{v\in Q(\Delta,\alpha)} \mathop{\rm dist}\nolimits (x(s^k(v),v),M^{\gamma})\le I^0(\Delta,\alpha)+K_2\frac{\mu_k}{t_k}.$$

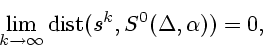
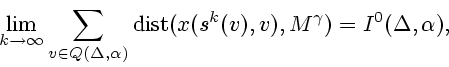
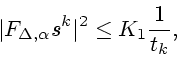
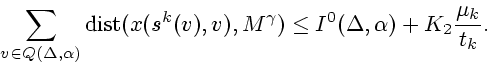
Опишем алгоритм (2.19), (2.12), (2.25), аппроксимирующий решение задачи (1.8), (1.3), (1.4).

Шаг 0. Для каждого $v\in Q(\Delta, \alpha)$

(a) находится вектор $l_{\gamma}^0(v\vert\Delta,\alpha)$ (2.18), максимизирующий на единичном шаре $L$ пространства $R^n$ функцию $l\longmapsto \kappa_{\gamma}(l,v\vert\Delta,\alpha)$ (2.17),

(б) при каждом $i=1,\ldots,m$ находится вектор $u_{\Delta,\alpha}(l_{\gamma}^0(v\vert\Delta,\alpha))_i$, минимизирующий на $P_{\alpha}$ функцию $u\longmapsto \left< (\Phi_i^{\Delta})'l,u\right>$ (см. (2.16)),

(в) при каждом $i=1,\ldots,m$ по формуле (2.19) определяется компонента $s^1(v)_i$ первого приближения $s^1$ к решению.

Шаг $k$ ($k\ge 1$).

1. По $k$-му приближению $s^k$ подсчитывается сумма

$$\sum_{v\in Q(\Delta,\alpha)} \mathop{\rm dist}\nolimits (x^k(s^k(v),v),M^{\gamma}),$$

аппроксимирующая оптимальное значение $I^0(\Delta,\alpha)$.

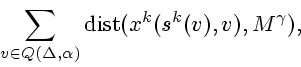
2. Для каждого $v\in Q(\Delta, \alpha)$

(a) по $k$-му приближению $s^k$ вычисляются суммы $\lambda_i(s,v\vert\Delta, \alpha)$ (2.22) ($i=1,\ldots,m$),

(б) находится вектор $l_{\gamma}^0(v\vert\Delta,\alpha)$ (2.18), максимизирующий на шаре $L$ функцию $l\longmapsto \kappa_{\gamma}(l,v\vert\Delta,\alpha)$ (2.17),

(в) при каждом $i=1,\ldots,m$ находится вектор $u_{\Delta,\alpha}(\lambda_i(s^k,v\vert\Delta,\alpha)+ \beta_k l_{\gamma}^0(v\vert\Delta,\alpha))_i$, минимизирующий на $P_{\alpha}$ функцию $u\longmapsto \left< (\Phi_i^{\Delta})'l,u\right>$,

(г) при каждом $i=1,\ldots,m$ по формуле (2.25) определяется компонента $\sigma^k(v)_i$ корректирующего элемента $\sigma^k$,

(д) при каждом $i=1,\ldots,m$ по формуле

$$s^{k+1}(v)_i=(1-\nu_k)s^k(v)_i+\nu_k\sigma^k(v)_i$$

(см. (2.12)) находится компонента $s^{k+1}(v)_i$ $(k+1)$-го приближения $s^{k+1}$.

Наборы элементарных операций (а)-(д) на шаге $k$ могут выполняться параллельно (независимо друг от друга) для всех $v\in Q(\Delta, \alpha)$. Такая параллелизуемость - основная черта предложенного алгоритма. Разумеется, большое количество параллельных вычислений (определяемое большим количеством элементов $v\in Q(\Delta, \alpha)$) не может не вызвать трудностей при практической реализации алгоритма. Для его адаптирования к практическим вычислениям требуется, прежде всего, как представляется, компактная кодировка запоминаемой на каждом шаге информации - текущего приближения $s^k$. В частности, может быть опробована та или иная кодировка $(\Delta,\alpha)$-управлений двоичными числами. Это, а также другие приемы практической адаптации алгоритма, могут послужить предметом отдельного исследования.

Поступила 7.12.99