3. Разбиение множества позиций в НПДИ

Введем следующие определения [7].

Определение 3.1   Позиция $(t_{\ast},x_{\ast})\in G$ называется неантаганистической ($NA$-позицией), если существует траектория системы $(\ref{f_1_1})$ $x(t),\\ t_{\ast}\leq t\leq\theta,\;x(t_{\ast})=x_{\ast}$ такая, что функции $\gamma_{i}(t,x(t)),\;i=1,2$ $(\ref{f_2_3})$ не убывают на $[t_{\ast },\theta]$ и по крайней мере для одного $j$ выполняется строгое неравенство

$$\gamma_{j}(\theta,x(\theta))>\gamma_{j}(t_{\ast},x_{\ast})$$ (3.1)

Рис. 1.

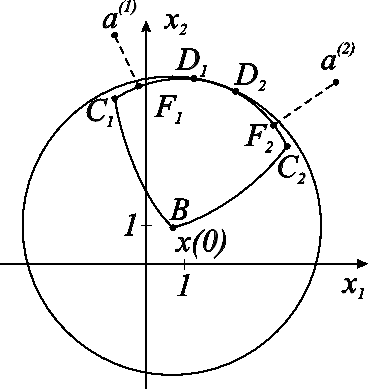
Определение 3.1 означает, что для начальной $NA$-позиции существует траектория, вдоль которой гарантированные выигрыши игроков не убывают и по крайней мере для одного игрока этот выигрыш в конце траектории строго больше, чем в $NA$-позиции. Эти траектории будем называть $NA$-траекториями. Для $NA$-позиции существует, вообще говоря, бесконечно много $NA$-траекторий.

Определение 3.2   Позиция $(t_{\ast},x_{\ast})\in G$ называется локально антагонистической ($LA$-позицией), если она не является неантагонистической и , кроме того, существует траектория системы $(\ref{f_1_1})$ $x(t)$, $t_{\ast}\leq t\leq\theta$,     $x(t_{\ast})=x_{\ast}$, вдоль которой выполнены следующие неравенства

$$\gamma_{i}(\theta,x(\theta))\geq\gamma_{i}(t,x(t)),\quad t_{\ast}\leq t\leq\theta,\quad i=1,2,$$ (3.2)

где по крайней мере одно неравенство является строгим при $t=t_{\ast}.$

Траектории из определения 3.2 будем называть $LA$-траекториями. Для $LA$-позиции существует, вообще говоря, бесконечно много $LA$-траекторий. Неравенства (3.2) указывают, что точка $t=\theta$ является точкой максимума обеих функций $\gamma_{1}(t,x)$ и $\gamma_{2}(t,x)$, вычисленных вдоль $LA$-траектории. Следовательно, в конце $LA$-траектории выигрыши обоих игроков будут не меньше, чем в начальной $LA$-позиции и хотя бы для одного игрока этот выигрыш будет строго больше.

Определение 3.3   Позиция $(t_{\ast},x_{\ast})\in G$ называется глобально антагонистической ($GA-$позицией), если для любой траектории системы
$(\ref{f_1_1})$ $\ x(t),\quad t_{\ast}\leq t\leq\theta,\quad x(t_{\ast})=x_{\ast}$ либо выполняется равенство

$$\gamma_{i}(\theta,x(\theta))=\gamma_{i}(t_{\ast},x_{\ast}),\quad i=1,2$$

либо по крайней мере для одного $j$ удовлетворяется неравенство

$$\gamma_{j}(\theta,x(\theta))<\gamma_{j}(\tau,x(\tau))$$

для всех $\tau\in\lbrack t_{\ast},\theta).$

Очевидно, для $GA$-позиции существует по крайней мере одна траектория, вдоль которой справедливы тождества

$$\gamma_{i}(t,x(t))\equiv\gamma_{i}(t_{\ast},x_{\ast}),\ \ \ t_{\ast}\leq t\leq\theta,\ \ \ i=1,2$$

Эта траектория называется $GA$-траекторией. Вообще говоря, может быть бесконечно много $GA$-траекторий. Все они находятся на поверхностях уровня функций $\gamma_{1}(t,x)$ и $\gamma_{2}(t,x)$ одновременно. Попутно отметим, что в $GA$-позициях оба игрока всегда достигают оптимальных по Парето выигрышей.

Легко видеть, что для $LA$-позиций, кроме $LA$-траекторий существуют также $GA$-траектории, а для $NA$-позиций, кроме $NA$-траекторий существуют $LA$-траектории и $GA$-траектории.

Таким образом, получено разбиение множества $G$ всех позиций в
НПДИ на три подмножества: подмножество $G_{1}$ всех $NA$-позиций, подмножество $G_{2}$ всех $LA$-позиций и подмножество $G_{3}$ всех $GA$-позиций.

Теорема 3.1   Если начальная позиция игры является $NA$-позицией, то $NE$-решение, $P^{\ast}$-решение и $H_{i}$-решение порождают либо $NA$-траекторию, либо $LA$-траекторию. Если начальная позиция является $LA$-позицией ($GA$-позицией), то $NE$-решение, $P^{\ast}$-решение и $H_{i}$-решение порождают $LA$-траекторию ( $GA$-траекторию).

Заметим, что в примере 2.1 множество $G_{3\text{ }}$ $GA$-позиций состоит из всех тех позиций $(t,x)\in G$, для которых $x$ принадлежит отрезку, соединяющему точки $a^{(1)}$ и $a^{(2)}$, а $t\in[t_{0} ,\theta]$. Множество $G_{1}$ $NA$-позиций включает все остальные позиции $(t,x)\in G$. Множество $G_{2}$ $LA$-позиций в этом примере пусто.

Пример разбиения множества $G$ на три непустых подмножества $G_{1},G_{2}$, $G_{3}$ можно найти в [7].