2. Вспомогательные антагонистические позиционные дифференциальные игры. Теоремы о структуре решений НПДИ

Рассмотрим теперь вспомогательные антагонистические позиционные дифференциальные игры $\Gamma_{1}$ и $\Gamma_{2}.$ Динамика обеих игр описывается уравнением (1.1). В игре $\Gamma_{i}$ игрок $i$ максимизирует функционал выигрыша $\sigma_{i}(x(\theta))$ (1.2) а игрок $3-i$ противодействует ему.

Пусть выполнено следующее предположение.

5$^{0}$. Функция $f(t,x,u,v)$ (1.1) удовлетворяет условию

$$\max\limits_{u\in P}\min\limits_{v\in Q}s^{T}f(t,x,u,v)=\min\limits_{v\in Q}\max\limits_{u\in P}s^{T}f(t,x,u,v)$$ (2.1)

для любых $s\in\mathbb{R}^{n}$ и $(t,x)\in G$.

Тогда из [2] следует, что обе игры $\Gamma_{1}$ и $\Gamma_{2}$ имеют универсальные седловые точки

$$\{u^{(i)}(t,x,\varepsilon),\ v^{(i)}(t,x,\varepsilon)\},\quad i=1,2,$$ (2.2)

и непрерывные функции цены

$$\gamma_{1}(t,x),\quad\gamma_{2}(t,x).$$ (2.3)

Свойство стратегий (2.2) быть универсальными означает, что они являются оптимальными не только для фиксированной начальной позиции
$(t_{0},x_{0})\in G$, но и для любой позиции $(t_{\ast},x_{\ast})\in G$, рассматриваемой в качестве начальной.

Теперь сформулируем следующие задачи.

Задача 2.1   Найти измеримые функции $u(t)$ и $v(t),\,t_{0}\leq t\leq\theta$, которые порождают траекторию $x(t),\;t_{0}\leq t\leq\theta$, удовлетворяющую неравенствам

$$\gamma_{i}(t,x(t))\leq\gamma_{i}(\theta,x(\theta)),\;t_{0}\leq t\leq \theta,\quad i=1,2$$ (2.4)

Задача 2.2   Для фиксированного $\alpha_{1}\in(0,1),\;\alpha_{2}=1-\alpha_{1}$ найти решение задачи $2.1$, которое максимизирует функционал выигрыша

$$\quad\min\limits_{i=1,2} \alpha_{i}\sigma_{i}(x(\theta)).$$

Задача 2.3   i ($i=1,2$). Найти решение задачи $2.1$, которое максимизирует функционал выигрыша $\sigma_{i}(x(\theta)).$

Задача 2.4   i ($i=1,2$). Найти измеримые функции $u(t)$ и $v(t),\;\ t_{0}\leq t\leq\theta$, которые порождают траекторию $x(t),\;t_{0}\leq t\leq\theta$, удовлетворяющую неравенству

$$\gamma_{3-i}(t,x(t))\leq\gamma_{3-i}(\theta,x(\theta)),\quad t_{0}\leq t\leq \theta$$ (2.5)

и максимизирует функционал выигрыша $\sigma_{i}(x(\theta)).$

Пусть кусочно-непрерывные функции $u^{\ast}(t)$ и $v^{\ast}(t),\;t_{0}\leq t\leq\theta$ порождают траекторию $x^{\ast}(t),\;t_{0}\leq t\leq\theta$ системы (1.1). Рассмотрим стратегии 1-го и 2-го игроков

$$U^{0}\div\{u^{0}(t,x,\varepsilon),\;\beta_{1}^{0}(\varepsilon)\},\quad V^{0}\div\{v^{0}(t,x,\varepsilon),\;\beta_{2}^{0}(\varepsilon)\},$$

где

$$\begin{array}[c]{c} u^{0}(t,x,\varepsilon)=\left\{ \begin{arr... ...\Vert \geq\varepsilon\varphi(t) \end{array} \right. \end{array}$$ (2.6)

для всех $t\in\lbrack t_{0},\theta].$ Функции $\beta_{i}(\cdot)$ и положительная возрастающая функция $\varphi(\cdot)$ выбраны так, что следующее неравенство

$$\left\Vert x(t,t_{0},x_{0},U^{0},\varepsilon,\Delta_{1},V^{0},\varepsilon ,\Delta_{2})-x^{\ast}(t))\right\Vert <\varepsilon\varphi(t)$$ (2.7)

имеет место для $\varepsilon>0,$ $\delta(\Delta_{i})\leq\beta_{i}(\varepsilon)$. Функции $u^{(2)}(\cdot)$ и $v^{(1)}(\cdot)$ определены в (2.2). Они могут быть интерпретированы как универсальные штрафные стратегии, используемые в случае, если партнер отказывается отслеживать траекторию $x^{\ast}(\cdot)$ в некоторый момент времени $t\in\lbrack t_{0},\theta].$ ''Стратегия наказания'' рассматривались в [4]-[6]].

6$^{0}$. Вектограмма системы (1.1)

$$F(t,x)=\{s\in\mathbb{R}:s=f(t,x,u,v),\ u\in P,\ v\in Q \}$$

выпукла в каждой точке $(t,x)\in G$.

Это предположение $\mathbb{\ }$ гарантирует, что множество достижимости системы (1.1), порожденное измеримыми управлениями, замкнуто относительно равномерной сходимости.

Справедливы следующие результаты [3].

Теорема 2.1   Пусть выполнены предположения $1^{0},\ 2^{0},\ 5^{0}$. Пусть
управления $u^{\ast}(\cdot)$ и $v^{\ast}(\cdot)$ доставляют решение задачи $2.1$ (или задачи $2.2$, $2.3.$i). Тогда пара стратегий $(U^{0},V^{0})$ $(\ref{f_2_6})$, $(\ref{f_2_7})$ образует $NE$-решение (или $P^{\ast}$-решение, $H_{i}$-решение). Наоборот, для любого $NE$-решения (или, при предположении $6^{0},P^{\ast}$-решения, $H_{i}$-решения) существует
эквивалентное решение того же типа, имеющее вид $(U^{0},V^{0})$ $(\ref{f_2_6})$, $(\ref{f_2_7})$ где $u^{\ast}(\cdot)$ и $v^{\ast}(\cdot)$ доставляют решение задачи $2.1$ (или задачи $2.2$, $2.3.i$, соответственно).

Теорема 2.2   Пусть выполнены предположения $1^{0}-6^{0}$. Пусть управления $u^{\ast}(\cdot)$ и $v^{\ast}(\cdot)$ доставляют решение задачи $2.4.i.$ Тогда пара стратегий $(U^{0},V^{0})$ $(\ref{f_2_6})$, $(\ref{f_2_7})$ образует $S_{i}$-решение. Наоборот, для любого $S_{i}$-решения существует эквивалентное ему $S_{i}$-решение , имеющее вид $(U^{0},V^{0})$ $(\ref{f_2_6})$, $(\ref{f_2_7})$ где $u^{\ast}(\cdot)$ и $v^{\ast}(\cdot)$ доставляют решение задачи $2.4.i.$

Таким образом, теоремы 2.1 и 2.2 устанавливают соответствия между множествами решений задач 2.1, 2.2, 2.3.i, 2.4.i и множествами $NE$-, $P^{\ast}$-, $H_{i}$-, и $S_{i}$-решений. Эти теоремы определяют структуру решений игры. Теоремы существования $NE$-, $P^{\ast}$-, $H_{i}$-, и $S_{i}$-решений являются следствиями теорем 2.1 и 2.2.

Пример 2.1   Векторное уравнение

$$\ddot{\xi}=u+v,\quad\xi,u,v\in\mathbb{R}^{2},\quad \left\Vert u\right\Vert \leq1,\;\left\Vert v\right\Vert \leq1$$ (2.8)

$$\xi\lbrack t_{0}]=\xi_{0},\;\;\dot{\xi}\lbrack t_{0}]=\xi_{0}$$

описывает движение материальной точки единичной массы в плоскости ( $\xi _{1},\xi_{2}$) под действием силы $F=u+v$. $1$-й игрок ($2$-й игрок), который распоряжается управлением $u\;(v)$, стремится максимизировать функционал выигрыша $\sigma _{1}(\xi\lbrack\theta])\;(\sigma_{2}(\xi\lbrack\theta]))$, где

$$\sigma_{i}(\xi\lbrack\theta])=-\left\Vert \xi\lbrack\theta]-a^{(i)}\right\Vert ,$$ (2.9)

$$\xi=(\xi_{1},\xi_{2}),\ \ \ a^{(i)}=(a_1^{(i)},\;a_2^{(i)}),\ \ i=1,2.$$

Здесь $a^{(i)},\; i=1,2$ - заданные точки в плоскости $(\xi_{1},\xi_{2})$; $\theta$ - момент окончания.

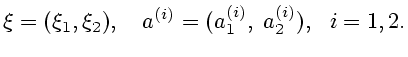
Обозначая $y_{1}=\xi_{1},\;y_{2}=\dot{\xi}_{1},\;y_{3}=\xi_{2},\;y_{4} =\dot{\xi}_{2}$ и производя замену переменных $x_{1}=y_{1}+(\theta-t)y_{3}$, $x_{2}=y_{2}+(\theta-t)y_{4}$, $x_{3}=y_{3}$, $x_{4}=y_{4}$, получим систему, два первых уравнения которой будут

$$\begin{array}[c]{c} \overset{\cdot}{x_{1}}=(\theta-t)(u_{1}+v... ...1ex] \overset{\cdot}{x_{2}}=(\theta-t)(u_{2}+v_{2}) \end{array}$$ (2.10)

Далее, (2.9) может быть переписано так

$$\sigma_{i}(x[\theta])=-\left\Vert x[\theta]-a^{(i)}\right\Vert ,\quad x=(x_{1} ,x_{2}),\ \ i=1,2$$ (2.11)

Так как функционал выигрыша (2.11) зависит только от переменных $x_{1}$ и $x_{2}$, а правая часть (2.10) не зависит от других переменных, можно заключить, что достаточно рассматривать только укороченную систему (2.10) с функционалами выигрыша (2.11).

Тогда начальные условия для системы (2.10) задаются формулами

$$x_{i}[t_{0}]=x_{0i}=\xi_{0i}-(\theta-t_{0})\dot{\xi}_{0i},\ \ \ i=1,2$$

Легко может быть показано, что функции цены антагонистических дифференциальных игр $\Gamma_{1}$ и $\Gamma_{2}$ задаются формулами

$$\gamma_{i}(t,x)=\left\Vert x-a^{(i)}\right\Vert ,\quad i=1,2,$$

а универсальные оптимальные стратегии (2.4)-формулами

$$u^{(i)}(t,x,\varepsilon)=-v^{(i)} (t,x,\varepsilon)=(-1)^{i}\frac{x-a^{(i)}}{\left\Vert x-a^{(i)}\right\Vert },\quad i=1,2.$$

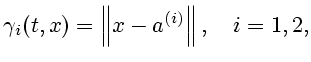
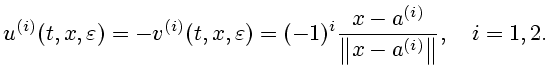
Пусть заданы следующие начальные условия и значения параметров: $t_{0}=0$, $\xi_{01}=2.2$, $\dot{\xi}_{01}=-0.8$, $\xi_{02}=1.3$, $\dot{\xi}_{02}=-0.2$, $\theta=2$, $a_{1}^{(1)}=-1$, $a_{2}^{(1)}=5$, $a_{1}^{(2)}=5$, $a_{2}^{(2)}=4$. Тогда имеем $x_{01} =6,\;x_{02}=0.9$.

Используя теоремы 2.1 и 2.2, можно построить решения игры. Мы опишем построенные множества $NE$-решений, $P^{\ast}$-решений, $H_{i}$-решений и $S_{i}$-решений через множества концов траекторий, порожденных этими решениями. На рис. 1 круг радиуса 4 с центром в начальной точке $B(0.6,0.9)$ представляет собою множество достижимости системы (2.10) в момент
$\theta=2$. Кривая $BC_{1}D_{1}D_{2}C_{2}B$ ограничивает множество концов траекторий, порожденных $NE$-решениями. Кривая $F_{1}D_{1}D_{2}F_{2}$ представляет собою множество концов траекторий для $P^{\ast}$-решений. Наконец, точка $F_{1}$ является единственной конечной точкой, порожденной $S_{1}$-решением и $H_{1}$-решением одновременно. Аналогично, точка $F_{2}$ является единственной конечной точкой, порожденной $S_{2}$-решением и $H_{2}$-решением одновременно. Заметим, что кривые $BC_{1}$ и $BC_{2}$ суть дуги окружностей с центрами в точках $a^{(2)}$ и $a^{(1)}$ соответственно.

Примечание 2.1   Возможно, $P^{\ast}$-решение является наиболее подходящим решением, которое не дает предпочтения какому-то игроку, как это имеет место, например, для $H_{i}$-решений. Однако, для $P^{\ast}$-решений мы имеем проблему выбора одного из них. Возможный алгоритм такого выбора, основанный на использовании вспомогательных биматричных игр, был предложен автором в [7]. Ниже в разделе 5 этот алгоритм будет приложен к построению динамики повторяющейся биматричной 2$\times$2 игры.