| (1.1) |
Пусть динамика
неантагонистической позиционной дифференциальной
игры (НПДИ) двух
лиц описывается уравнением
Пусть ![]() - компакт в
- компакт в
![]() ,
проекция которого на ось времени равна заданному отрезку
,
проекция которого на ось времени равна заданному отрезку
![]() . Предполагаем, что все траектории системы
(1.1), начинающиеся в произвольной позиции
. Предполагаем, что все траектории системы
(1.1), начинающиеся в произвольной позиции
![]() , остаются в
, остаются в ![]() при всех
при всех
![]() .
.
Пусть выполнены следующие предположения.
1![]() . Функция
. Функция
![]() непрерывна на множестве аргументов и удовлетворяет условию Липшица
по
непрерывна на множестве аргументов и удовлетворяет условию Липшица
по ![]() .
.
2![]() . Существует константа
. Существует константа ![]() такая, что
такая, что
Игрок ![]() выбирает свое управление, чтобы максимизировать
функционал выигрыша
выбирает свое управление, чтобы максимизировать
функционал выигрыша
Предположим, что оба игрока имеют полную информацию о текущей
позиции ![]() игры. Формализация стратегии игроков и
порождаемых ими движений в НПДИ та же, что и формализация,
введенная в антагонистических позиционных дифференциальных играх
[1,2] за исключением технических деталей [3]. Чистая
стратегия (кратко - стратегия) 1-го игрока отождествляется с парой
игры. Формализация стратегии игроков и
порождаемых ими движений в НПДИ та же, что и формализация,
введенная в антагонистических позиционных дифференциальных играх
[1,2] за исключением технических деталей [3]. Чистая
стратегия (кратко - стратегия) 1-го игрока отождествляется с парой
![]() , где
, где
![]() - произвольная функция, зависящая от позиции
- произвольная функция, зависящая от позиции ![]() и
от положительного параметра точности
и
от положительного параметра точности
![]() и имеющая
значения во множестве
и имеющая
значения во множестве ![]() . Функция
. Функция
![]() - непрерывная, монотонная,
удовлетворяющая условию
- непрерывная, монотонная,
удовлетворяющая условию
![]() при
при
![]() . Функция
. Функция
![]() имеет
следующий смысл. Для фиксированного
имеет
следующий смысл. Для фиксированного
![]() величина
величина
![]() представляет собою верхнюю грань для шага
разбиения отрезка
представляет собою верхнюю грань для шага
разбиения отрезка
![]() , которое 1-й игрок использует
при формировании пошагового движения. Стратегия
, которое 1-й игрок использует
при формировании пошагового движения. Стратегия
![]() 2-го игрока
определяется аналогично.
2-го игрока
определяется аналогично.
Движения двух типов: аппроксимационные (пошаговые) и идеальные
(предельные) рассматриваются в качестве движений, порожденных
стратегиями игроков. Аппроксимационное движение ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() вводится для фиксированных
значений параметров точности
вводится для фиксированных
значений параметров точности
![]() и
и
![]() и для фиксированных разбиений
и для фиксированных разбиений
![]() и
и
![]() отрезка
отрезка
![]() , выбираемых
1-ым и 2-ым игроками, соответственно, при условии
, выбираемых
1-ым и 2-ым игроками, соответственно, при условии
![]() )
)
![]() Здесь
Здесь
![]() Предельное движение , порожденное парой стратегий
Предельное движение , порожденное парой стратегий ![]() из
начальной позиции
из
начальной позиции
![]() , есть непрерывная функция
, есть непрерывная функция
![]() , для которой существует
последовательность аппроксимационных движений
, для которой существует
последовательность аппроксимационных движений
![$\displaystyle \{x[t,t_{0}^{k},x_{0}^{k},U,\varepsilon_{1}^{k},\Delta_{1}^{k},V,\varepsilon
_{2}^{k},\Delta_{2}^{k}]\},$](img54.gif)
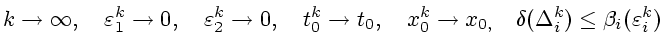 .
.
Пара стратегий ![]() порождает непустое компактное (в метрике
пространства
порождает непустое компактное (в метрике
пространства
![]() множество
множество
![]() ,
состоящие из предельных движений
,
состоящие из предельных движений
![]()
Введем теперь следующие определения [3].
![$\displaystyle \max_{x[\cdot]}\sigma_{1}(x[\theta,\tau,x^{\ast}[\tau],U,V^{N}])\leq\sigma
_{1}(x[\theta,\tau,x^{\ast}[\tau],U^{N},V^{N}]),
$](img66.gif)
![$\displaystyle \max_{x[\cdot]}\sigma_{2}(x[\theta,\tau,x^{\ast}[\tau],U^{N},V])\leq\sigma
_{2}(x[\theta,\tau,x^{\ast}[\tau],U^{N},V^{N}]) $](img67.gif)
Пусть теперь выполнены следующие предположения.
3![]() 1-й игрок, называемый лидером, объявляет свою стратегию
1-й игрок, называемый лидером, объявляет свою стратегию
![]() 2-му игроку наперед.
2-му игроку наперед.
4![]() . 2-й игрок, называемый ведомым, имея в виду стратегию
. 2-й игрок, называемый ведомым, имея в виду стратегию ![]() 1-го игрока, выбирает свою рациональную стратегию
1-го игрока, выбирает свою рациональную стратегию ![]() из условия
из условия
Задача 1-го игрока заключается в нахождении такой стратегии
![]() , которая гарантирует ему максимальное значение
функционала выигрыша
, которая гарантирует ему максимальное значение
функционала выигрыша
![]() (1.2) при
условии рациональности 2-го игрока. (более детальная постановка,
включающая рассмотрение различных вариантов выбора из множества
рациональных стратегий 2-го игрока, содержится в [3]).
(1.2) при
условии рациональности 2-го игрока. (более детальная постановка,
включающая рассмотрение различных вариантов выбора из множества
рациональных стратегий 2-го игрока, содержится в [3]).
![]() -решение определяется аналогично.
-решение определяется аналогично.