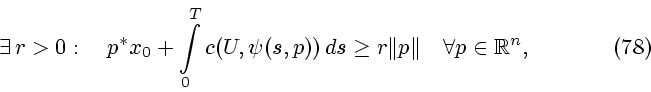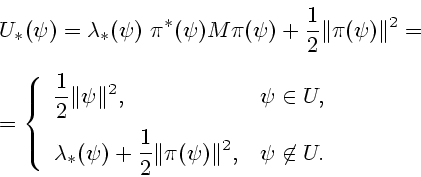

Next: Bibliography
Up: KISELEV
Previous: 3 Линейная задача быстродействия
Рассмотрим задачу оптимального управления
Здесь
 -
- 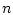 -мерный фазовый вектор;
-мерный фазовый вектор;
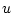 -
- 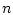 -мерное управление, которое принимает значения
из эллипсоидальной области управления
-мерное управление, которое принимает значения
из эллипсоидальной области управления 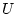 , размеры и форма которой
определяются симметричной положительно определенной матрицей
, размеры и форма которой
определяются симметричной положительно определенной матрицей 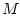 порядка
порядка 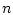 ;
;
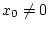 - заданное начальное состояние управляемого объекта;
- заданное начальное состояние управляемого объекта;
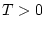 - заданная длительность процесса управления,
подчиненная неравенству
- заданная длительность процесса управления,
подчиненная неравенству
где 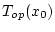 - время быстродействия рассматриваемой управляемой системы
из начального состояния
- время быстродействия рассматриваемой управляемой системы
из начального состояния 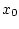 в начало координат.
в начало координат.
Требуется найти: оптимальное управление
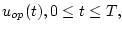 оптимальную траекторию
оптимальную траекторию
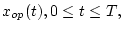 и оптимальное значение функционала
и оптимальное значение функционала 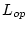 . Для решения задачи (43)
применяется принцип максимума Понтрягина.
. Для решения задачи (43)
применяется принцип максимума Понтрягина.
Выпишем функцию Гамильтона-Понтрягина и положим 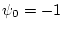 :
:
Из условия максимума
найдем экстремальное управление (максимизатор функции  по аргументу
по аргументу
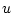 на множестве
на множестве 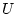 )
)
Нам необходимо более подробное изучение функции (45).
Рассматривая вспомогательную задачу безусловной
максимизации функции 
найдем ее решение (максимизатор функции  по аргументу
по аргументу  на всем
пространстве)
на всем
пространстве)
привлекая уравнение
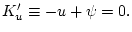 Этот же результат становится очевидным, если представить функцию
Этот же результат становится очевидным, если представить функцию 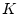 в форме
в форме
Поэтому
где 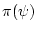 - проекция внешней по отношению к множеству
- проекция внешней по отношению к множеству 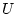 точки
точки
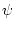 на это множество
на это множество 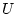 . Это утверждение вытекает из того, что
поверхностями уровня функции
. Это утверждение вытекает из того, что
поверхностями уровня функции 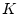 (в пространстве аргумента
(в пространстве аргумента 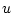 ) являются
сферы
) являются
сферы
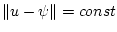 с центром в точке
с центром в точке 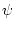 , см. (46). Напомним, что под проекцией точки на
множество понимается точка множества, наименее удаленная от проектируемой
точки. Таким образом,
, см. (46). Напомним, что под проекцией точки на
множество понимается точка множества, наименее удаленная от проектируемой
точки. Таким образом,
причем
Функция
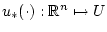 из (45)
определена и непрерывна на всем пространстве
из (45)
определена и непрерывна на всем пространстве
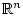 и является гладкой на
и является гладкой на
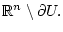 На границе
На границе
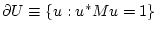 области управления
области управления 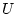 гладкость этой функции нарушается. Привлекая
экстремальное управление (45), запишем краевую задачу принципа максимума
для задачи оптимального управления (43):
гладкость этой функции нарушается. Привлекая
экстремальное управление (45), запишем краевую задачу принципа максимума
для задачи оптимального управления (43):
Эта краевая задача нелинейна, поскольку нелинейна функция (45),
описывающая экстремальное управление. Алгоритм вычисления этой функции
описан в следующем подразделе.
Рассмотрим задачу вычисления проекции 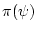 точки
точки 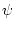 на
эллипсоид
на
эллипсоид 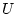 (п. 4.1). Если
(п. 4.1). Если 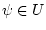 , то
, то
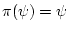 . Поэтому ниже
рассматривается основной случай
. Поэтому ниже
рассматривается основной случай
Так как вектор
определяет внешнюю нормаль к 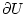 в точке
в точке
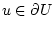 и
и
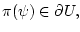 то имеет место равенство
то имеет место равенство
при некотором положительном числе 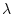 . Отсюда следует, что
. Отсюда следует, что
где 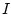 - единичная матрица.
Условие принадлежности точки (50) границе эллипсоида
- единичная матрица.
Условие принадлежности точки (50) границе эллипсоида 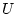 приводит к
следующему уравнению для вычисления параметра
приводит к
следующему уравнению для вычисления параметра 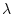 :
:
Здесь
Функция (52) обладает следующими свойствами:
Поэтому уравнение (51) имеет единственный положительный корень
Этот корень может быть вычислен с помощью итерационного процесса Ньютона
Таким образом, имеет место следующее утверждение.
Теорема 1. Если 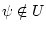 , то проекция
, то проекция 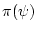 точки
точки 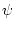 на эллипсоид
на эллипсоид 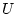 допускает представление
допускает представление
где
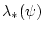 - единственный положительный корень уравнения
- единственный положительный корень уравнения 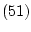 ,
который может быть вычислен итерационным процессом
,
который может быть вычислен итерационным процессом 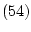 .
.
З а м е ч а н и е 1. Доопределим функцию
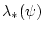 на все
пространство, полагая
на все
пространство, полагая
Теперь функция
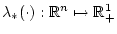 определена и
непрерывна
во всем пространстве, а ее градиент
определена и
непрерывна
во всем пространстве, а ее градиент
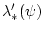 имеет конечный
скачок на границе эллипсоида
имеет конечный
скачок на границе эллипсоида 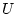 .
Таким образом, при любом векторе
.
Таким образом, при любом векторе
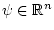 проекция
проекция 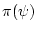 допускает представление (55). Исследованное выше экстремальное управление
допускает представление (55). Исследованное выше экстремальное управление
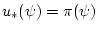 можно рассматривать как многомерный аналог, связанный с эллипсоидом
можно рассматривать как многомерный аналог, связанный с эллипсоидом 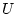 ,
функции насыщения (18),
с помощью которой записывалось экстремальное управление
в задаче (1а).
,
функции насыщения (18),
с помощью которой записывалось экстремальное управление
в задаче (1а).
З а м е ч а н и е 2. В работе [14] рассмотрена нелинейная версия
метода Ньютона для вычисления проекции на эллипсоид на основе
дробно-рациональной аппроксимации функции 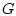 .
Эта версия имеет ряд преимуществ
перед классической схемой (54). Сравнение различных
вычислительных схем для поиска проекции можно найти в работе [15].
.
Эта версия имеет ряд преимуществ
перед классической схемой (54). Сравнение различных
вычислительных схем для поиска проекции можно найти в работе [15].
Введем обозначение
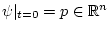 для начального значения сопряженной переменной.
Решить краевую
задачу (3) - значит, найти такой вектор
для начального значения сопряженной переменной.
Решить краевую
задачу (3) - значит, найти такой вектор 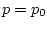 , который
позволяет свести задачу к решению задач Коши, а задачу Коши можно
рассматривать как стандартную вычислительную задачу.
Для параметра
, который
позволяет свести задачу к решению задач Коши, а задачу Коши можно
рассматривать как стандартную вычислительную задачу.
Для параметра 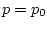 будет установлено экстремальное описание
будет установлено экстремальное описание
где 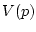 - гладкая выпуклая функция, которую будем называть
потенциалом задачи (43). Функция
- гладкая выпуклая функция, которую будем называть
потенциалом задачи (43). Функция 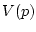 , которая ниже будет описана
конструктивно, строится по исходным данным задачи (43). Таким образом,
разрешающий параметр
, которая ниже будет описана
конструктивно, строится по исходным данным задачи (43). Таким образом,
разрешающий параметр 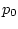 является минимизатором
в задаче безусловной выпуклой минимизации
является минимизатором
в задаче безусловной выпуклой минимизации
Задача (57) является одной из простейших задач математического
программирования, для решения которой можно пользоваться широким
спектром методов конечномерной безусловной оптимизации.
В результате этих рассуждений мы видим, что применение принципа максимума
Понтрягина к задаче оптимального управления (43) сводит проблему построения
оптимального управления (функции) к конечномерной задаче минимизации (57)
для отыскания параметра
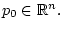 Обратимся сейчас к
построению потенциала задачи (43).
Обратимся сейчас к
построению потенциала задачи (43).
Задача Коши для сопряженного уравнения
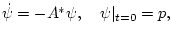 имеет решение
имеет решение
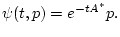 Подстановка этого решения в первое уравнение задачи (47) приводит,
вместе с ее начальным условием, к следующей задаче Коши
Подстановка этого решения в первое уравнение задачи (47) приводит,
вместе с ее начальным условием, к следующей задаче Коши
Решение этой задачи, линейной по 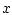 , запишем, используя формулу Коши:
, запишем, используя формулу Коши:
Требование, чтобы последняя функция удовлетворяла второму краевому условию
задачи (47), приводит к следующему векторному уравнению для определения
неизвестного вектора 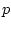 :
:
Уравнение (59), в силу (58),
равносильно следующему уравнению, имеющему градиентную форму:
Утверждение о градиентной форме уравнения (60) является следствием
градиентного свойства экстремального управления 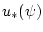 .
.
Теорема 2. Существует единственная гладкая выпуклая функция
с непрерывным градиентом
Функция 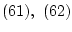 определяется следующей формулой
определяется следующей формулой
где 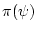 - проекция точки
- проекция точки 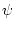 на эллипсоид
на эллипсоид 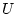 .
.
Д о к а з а т е л ь с т в о. Тот факт, что (63) влечет (61), (62) установлен в [16, леммы 4.2-4.4].
Теперь докажем обратное утврждение.
При 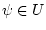 справедливы равенства
справедливы равенства
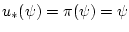 (см. (46)). Отсюда показывается, что
единственной функцией, удовлетворяющей условиям (61), (62) при
(см. (46)). Отсюда показывается, что
единственной функцией, удовлетворяющей условиям (61), (62) при
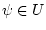 , будет функция
, будет функция
Пусть теперь 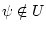 . Заметим, что на луче
. Заметим, что на луче
проекция сохраняет постоянное значение:
Запишем 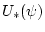 в форме
в форме
Последний член в (65) в силу включения
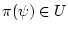 может быть
представлен в виде
может быть
представлен в виде
Остается вычислить приращение
функции (61) на луче 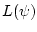 .
.
Привлекая (64), (62), получаем:
Последнее соотношение вместе с (65), (66) приводит к выражению (63).
Таким образом,
Выпуклость этой функции проверяется следующей выкладкой:
(детали можно восстановить, обратившись к доказательству следующей ниже
теоремы 3). Теорема 2 доказана.
Лемма. Справедливы утверждения:
(a)
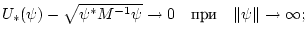
(b) существует положительное число 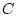 такое, что
такое, что
(c) имеет место следующее неравенство
где
Д о к а з а т е л ь с т в о. В силу (55) можно записать равенство
Далее считаем
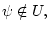 тогда
тогда
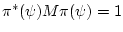 и, в силу (68), получаем
и, в силу (68), получаем
причем проекция
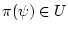 ограничена. По геометрическим
соображениям,
ограничена. По геометрическим
соображениям,
Привлекая (55), имеем
Из (63), (69), (70), считая по-прежнему 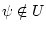 , имеем
, имеем
Отсюда, в силу ограниченности проекции 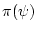 и
предельного соотношения (70), следует (a).
Тогда из непрерывности функции
и
предельного соотношения (70), следует (a).
Тогда из непрерывности функции
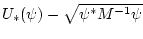 следует ограниченность этой функции во всем пространстве, т.е. имеет место
(b), а следовательно, и (c).
следует ограниченность этой функции во всем пространстве, т.е. имеет место
(b), а следовательно, и (c).
Теорема 3. Потенциал задачи 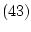 имеет вид
имеет вид
где функция 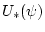 - потенциал экстремального управления
- потенциал экстремального управления
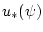
 см.
см. 
 - описана в теореме
- описана в теореме 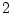 . Функция
. Функция 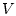 выпукла и
неогpаниченно растет при
выпукла и
неогpаниченно растет при
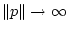
 см. (73)).
см. (73)).
Д о к а з а т е л ь с т в о. Функция (73)
имеет непрерывный градиент 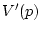 (см. (60))
(см. (60))
Нужно доказать выпуклость функции 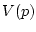 и свойство
и свойство
Выпуклость функции 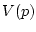 следует из неравенства
следует из неравенства
Действительно, из условия максимума для экстремального управления (45)
следует неравенство
которое запишем в форме
Полагая в последнем неравенстве сначала
затем
и складывая полученные неравенства, находим:
Далее, привлекая (74) и (77), имеем
Неравенство (76) доказано, и, тем самым, выпуклость функции 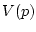 проверена.
проверена.
Докажем теперь (75). Предположение (44) влечет утверждение:
где
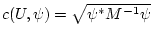 - опорная функция эллипсоида
- опорная функция эллипсоида
 , см. (43). Привлекая (78), запишем для функции (73) оценку снизу
, см. (43). Привлекая (78), запишем для функции (73) оценку снизу
Для завершения доказательства заметим, что
из неравенств (79) и (67) следует
что влечет за собой соотношение (75).
Теорема 3 доказана.
2
В заключение отметим следующую формулу для функции (63):
Поступила 17.02.1998


Next: Bibliography
Up: KISELEV
Previous: 3 Линейная задача быстродействия
2003-08-11
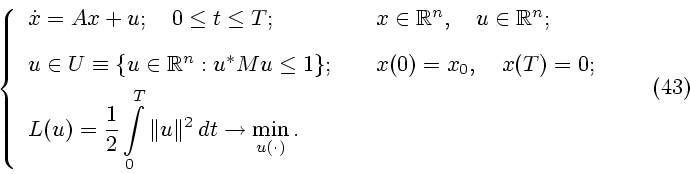
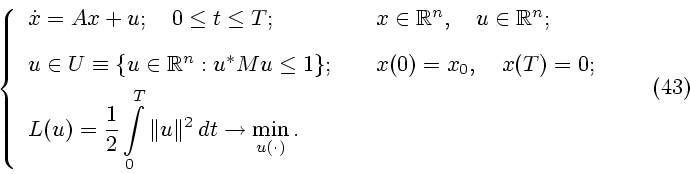
![]() оптимальную траекторию
оптимальную траекторию
![]() и оптимальное значение функционала
и оптимальное значение функционала ![]() . Для решения задачи (43)
применяется принцип максимума Понтрягина.
. Для решения задачи (43)
применяется принцип максимума Понтрягина.
![]() :
:
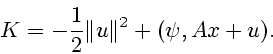
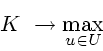
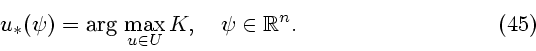
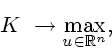
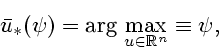
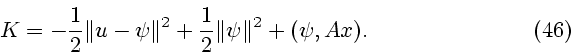
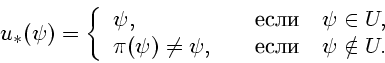
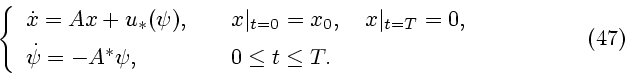
![]() точки
точки ![]() на
эллипсоид
на
эллипсоид ![]() (п. 4.1). Если
(п. 4.1). Если ![]() , то
, то
![]() . Поэтому ниже
рассматривается основной случай
. Поэтому ниже
рассматривается основной случай
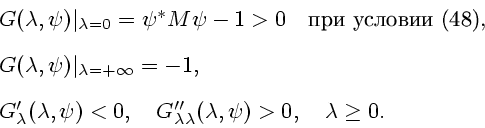
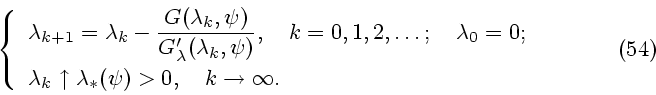
![]() , то проекция
, то проекция ![]() точки
точки ![]() на эллипсоид
на эллипсоид ![]() допускает представление
допускает представление
![]() на все
пространство, полагая
на все
пространство, полагая
![]() .
Эта версия имеет ряд преимуществ
перед классической схемой (54). Сравнение различных
вычислительных схем для поиска проекции можно найти в работе [15].
.
Эта версия имеет ряд преимуществ
перед классической схемой (54). Сравнение различных
вычислительных схем для поиска проекции можно найти в работе [15].
![]() для начального значения сопряженной переменной.
Решить краевую
задачу (3) - значит, найти такой вектор
для начального значения сопряженной переменной.
Решить краевую
задачу (3) - значит, найти такой вектор ![]() , который
позволяет свести задачу к решению задач Коши, а задачу Коши можно
рассматривать как стандартную вычислительную задачу.
Для параметра
, который
позволяет свести задачу к решению задач Коши, а задачу Коши можно
рассматривать как стандартную вычислительную задачу.
Для параметра ![]() будет установлено экстремальное описание
будет установлено экстремальное описание


![]() Обратимся сейчас к
построению потенциала задачи (43).
Обратимся сейчас к
построению потенциала задачи (43).
![]() имеет решение
имеет решение
![]() Подстановка этого решения в первое уравнение задачи (47) приводит,
вместе с ее начальным условием, к следующей задаче Коши
Подстановка этого решения в первое уравнение задачи (47) приводит,
вместе с ее начальным условием, к следующей задаче Коши
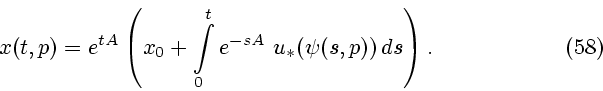
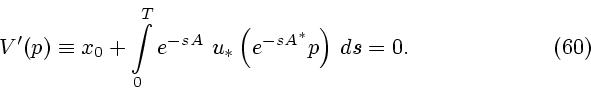
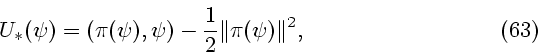
![]() справедливы равенства
справедливы равенства
![]() (см. (46)). Отсюда показывается, что
единственной функцией, удовлетворяющей условиям (61), (62) при
(см. (46)). Отсюда показывается, что
единственной функцией, удовлетворяющей условиям (61), (62) при
![]() , будет функция
, будет функция
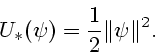

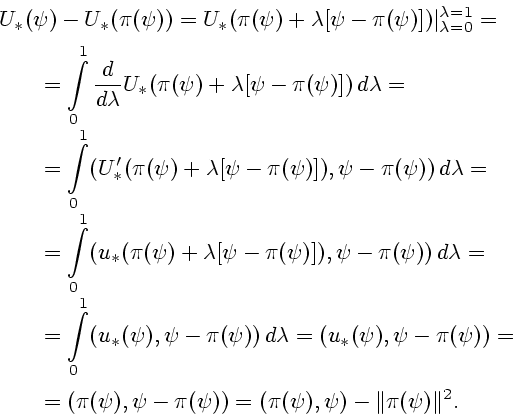
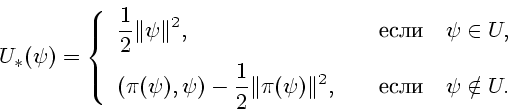
![\begin{displaymath}
\begin{array}{l}
[\psi - \chi]^* [U_*'(\psi) - U_*'(\chi)] ...
...-u_*(\chi)] +
\chi^* [u_*(\chi)- u_*(\psi)] \ge 0;
\end{array}\end{displaymath}](img227.gif)
![]()
![]() такое, что
такое, что
![\begin{displaymath}
R(p) = \int\limits_0^T \left[\ U_* (\psi) - \sqrt{\psi^* M^{-1} \psi} \
\right]_{\psi = \psi (s,p)} \, ds.
\end{displaymath}](img232.gif)
![\begin{displaymath}
\begin{array}{l}
{ \psi^* M^{-1} \psi }
= { \pi (\psi)^* [I+...
... (\psi) - \Vert \pi (\psi) \Vert^4
]
}.
\end{array}\eqno{(71)}
\end{displaymath}](img238.gif)
![\begin{displaymath}-
{\displaystyle {\pi^* (\psi) M^{-1} \pi (\psi) - \Vert \pi ...
...\pi^* (\psi) M^{-1} \pi (\psi) - \Vert \pi (\psi) \Vert^4]}}}
-\end{displaymath}](img240.gif)

![]() имеет вид
имеет вид
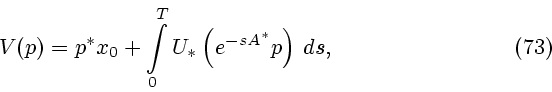
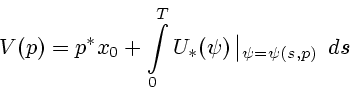
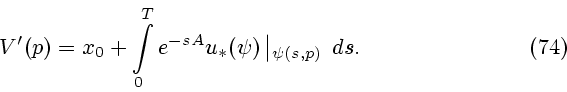
![]() следует из неравенства
следует из неравенства
![\begin{displaymath}
\psi^* [u_*(\psi) -v] \ge \frac{1}{2} \Vert u_*(\psi) \Vert^2 -
\frac{1}{2} \Vert v \Vert^2 \quad \forall v
\in U.
\end{displaymath}](img256.gif)
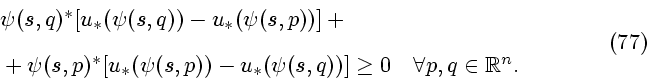
![\begin{displaymath}
\begin{array}{l}
[q-p]^* [V'(q) -V'(p)]= \\ [2ex]
\displayst...
...,p) ) - u_* ( \psi (s,q) ) ] \right\}
\, ds \ge 0.
\end{array}\end{displaymath}](img260.gif)