| (5.1) |
Рассмотрим задачу
оценивания входа линейной динамической системы по результатам
наблюдения выхода. Вход и выход системы будем считать скалярными.
Пусть уравнение системы имеет вид
| (5.2) |
Оператор ![]() здесь определяется равенством
здесь определяется равенством ![]() , где
координаты вектора
, где
координаты вектора ![]() находятся из соотношений
находятся из соотношений
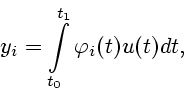
Пусть требуется оценить величину
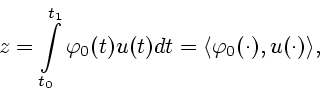
Обозначим через ![]() матрицу Грама системы функций
матрицу Грама системы функций
![]() . Пусть
. Пусть
Оценки уклонения
![]() от
от
![]() могут быть получены из следствия 2.1, где
могут быть получены из следствия 2.1, где
![]() - решения следующих задач квадратичного
программирования
- решения следующих задач квадратичного
программирования
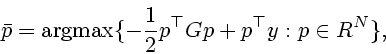
Рисунок приведен для системы
![]() при
при ![]() . Здесь показаны графики
зависимости величин
. Здесь показаны графики
зависимости величин
![]() (маркированные как
(маркированные как ![]() ), и их оценок
), и их оценок
![]() ,
,
![]() (маркированные как
(маркированные как
![]() ) от величины
) от величины ![]() . Величина
. Величина ![]() выбиралась равной
выбиралась равной
![]() . Границы
. Границы ![]() изображены сплошной линией,
график
изображены сплошной линией,
график
![]() отмечен звездочками.
отмечен звездочками.
Заметим, что для рассматриваемого примера условие (2.12) будет
выполнено, если ![]() и
и
![]() . Для задачи оценивания состояния
(
. Для задачи оценивания состояния
(
![]() ) (2.12) выполнено, если
) (2.12) выполнено, если ![]() и система (5.1) вполне управляема.
и система (5.1) вполне управляема.
![\includegraphics[width=0.8\textwidth,height=0.35\textheight]{c:/marinov/tom6rus/final2/gusev/estf.eps}](img414.gif)
Поступила
03.08.96