Распространим полученные оценки на случай, когда оператор
Распространим полученные оценки на случай, когда оператор ![]() задан с погрешностью. Предположим, что вместо
задан с погрешностью. Предположим, что вместо ![]() известен
оператор
известен
оператор ![]() такой, что
такой, что
![]()
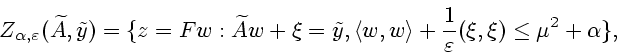
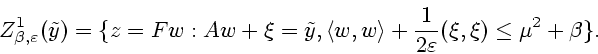
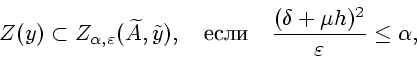
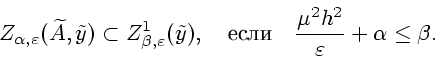
Первое из включений следует непосредственно из определения. Для
доказательства второго включения выберем
![]() Найдутся
Найдутся ![]() такие, что
такие, что
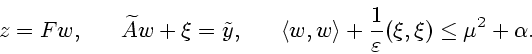
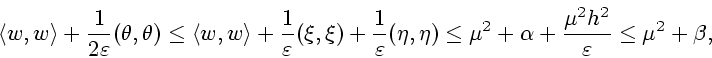
Обозначим через