Для произвольного множества ![]() в линейном нормированном
пространстве
в линейном нормированном
пространстве ![]() через
через ![]() обозначим опорную функцию
обозначим опорную функцию
![]() .
.
Пусть
![]() , тогда
, тогда ![]() и, значит
и, значит ![]() .
Так как
.
Так как
![]() , то из симметричности
, то из симметричности ![]() относительно
относительно
![]() следует, что
следует, что
![]() . Таким
образом,
. Таким
образом,
![]() . Отсюда, учитывая условие
. Отсюда, учитывая условие ![]() , получим неравенство (2.1). Пусть
, получим неравенство (2.1). Пусть
![]() .
Тогда
.
Тогда
![]() в силу выпуклости
в силу выпуклости ![]() , следовательно,
, следовательно,
![]() .
.
Для оценки величины
![]() воспользуемся формулами (1.8)-(1.12). Обозначим
воспользуемся формулами (1.8)-(1.12). Обозначим
![]() . Тогда (1.8) примет вид
. Тогда (1.8) примет вид
Из (1.12) следует, что
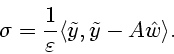
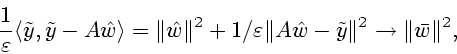
Если
![]() , то из (2.4) получим
, то из (2.4) получим
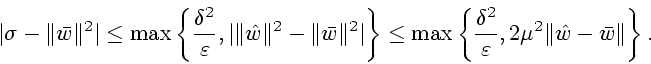
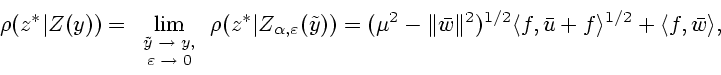
Заметим, что
![]() .
Действительно, так как
.
Действительно, так как ![]() и
и ![]() удовлетворяют уравнению
удовлетворяют уравнению
![]() , то этому уравнению удовлетворяет и
, то этому уравнению удовлетворяет и
![]() . Приравнивая нулю производную
. Приравнивая нулю производную
![]() в точке минимума
в точке минимума ![]() , получим искомое равенство.
, получим искомое равенство.
Учитывая неравенства
![]() ,
,
![]() , получим
, получим
Таким образом, оценки уклонения
![]() и, следовательно,
и, следовательно,
![]() от
от ![]() сводятся к оценкам скорости
сходимости регуляризаторов Тихонова
сводятся к оценкам скорости
сходимости регуляризаторов Тихонова ![]() и
и
![]() к нормальным решениям
к нормальным решениям ![]() и
и ![]() уравнений
уравнений ![]() ,
,
![]() соответственно. Предположим, что
соответственно. Предположим, что ![]() и
и ![]() истокообразно представимы, то есть существуют
истокообразно представимы, то есть существуют
![]() , такие что
, такие что
![]() . В
этом случае
(см.,например,[14,15])
. В
этом случае
(см.,например,[14,15])
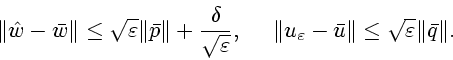
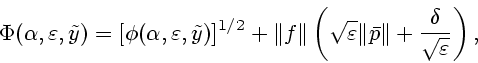
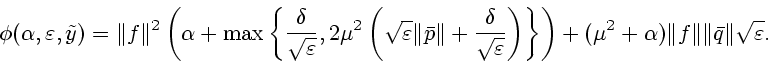
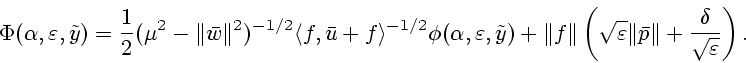
При выборе
![]() получаем
получаем
Условие истокообразной представимости ![]() является достаточно
сильным условием. Оно не всегда выполняется, если, например,
оператор
является достаточно
сильным условием. Оно не всегда выполняется, если, например,
оператор ![]() есть оператор вход-выход для линейной динамической
системы вида (1.6), (1.7) (при
есть оператор вход-выход для линейной динамической
системы вида (1.6), (1.7) (при
![]() ,
,
![]() ,
,
![]() ,
, ![]() ). В
[12] применительно к задаче восстановления входа линейной
динамической системы предложено ослабление условий истокообразной
представимости, при выполнении которых оценка уклонения
). В
[12] применительно к задаче восстановления входа линейной
динамической системы предложено ослабление условий истокообразной
представимости, при выполнении которых оценка уклонения ![]() от
от ![]() имеет порядок
имеет порядок
![]() для некоторого
натурального числа
для некоторого
натурального числа ![]() .
.
Оценка погрешности может быть улучшена, если оператор
![]() нормально разрешим, то есть имеет замкнутую область значений
нормально разрешим, то есть имеет замкнутую область значений
![]() . В этом случае (см.[14]) найдутся константы
. В этом случае (см.[14]) найдутся константы
![]() , не зависящие от
, не зависящие от
![]() , такие что
, такие что
Отметим, что для нормально разрешимого оператора выполнение
равенств
![]() для некоторого
для некоторого ![]() необходимо и достаточно для того, чтобы
необходимо и достаточно для того, чтобы ![]() было
нормальным решением уравнения
было
нормальным решением уравнения ![]() . Условие
. Условие
![]() ,
фигурирующее в теореме 1, заменим более сильным условием
,
фигурирующее в теореме 1, заменим более сильным условием
При выборе
![]() получаем
получаем
Заметим, что оператор ![]() нормально разрешим, если пространства
нормально разрешим, если пространства
![]() или
или ![]() конечномерны. В следующем разделе рассматривается
случай конечномерного
конечномерны. В следующем разделе рассматривается
случай конечномерного ![]() , при этом дается прямой вывод оценок
погрешности, основанный на использовании теорем двойственности в
задачах выпуклого программирования, и уточняются константы,
фигурирующие в оценках.
, при этом дается прямой вывод оценок
погрешности, основанный на использовании теорем двойственности в
задачах выпуклого программирования, и уточняются константы,
фигурирующие в оценках.