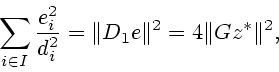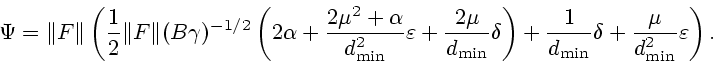

Next: 4 Случай оператора, заданного
Up: GUSEV
Previous: 2 Бесконечномерные наблюдения
Итак, пусть
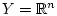 ,
, 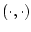 обозначает
скалярное произведение в
обозначает
скалярное произведение в 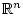 ,
,
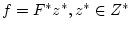 .
Величины
.
Величины
определяются из
решения следующих экстремальных задач:
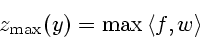 |
(3.1) |
при ограничениях
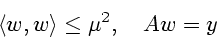 |
(3.2) |
и
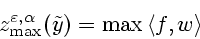 |
(3.3) |
при ограничениях
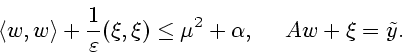 |
(3.4) |
Найдем
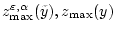 из
решения двойственных экстремальных задач. Из теоремы
двойственности для задач выпуклого программирования [13]
следует, что
из
решения двойственных экстремальных задач. Из теоремы
двойственности для задач выпуклого программирования [13]
следует, что
где
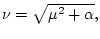
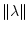 - евклидова норма в
- евклидова норма в 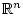 .
Величины нижних граней в приведенных выражениях конечны.
.
Величины нижних граней в приведенных выражениях конечны.
Представим
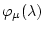 в следующем виде:
в следующем виде:
где 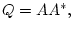
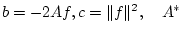 - сопряженный к
- сопряженный к 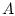 оператор.
оператор.
Учитывая, что 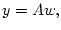
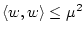 ,
имеем
,
имеем
Пусть 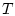 -
ортогональное преобразование, приводящее
-
ортогональное преобразование, приводящее 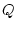 к диагональному виду:
к диагональному виду:
После замены 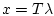 получим
получим
Обозначим
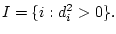 Из условия
Из условия
следует 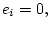
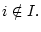 В силу того, что
В силу того, что
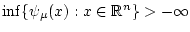 имеем
имеем
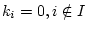 , и
, и
откуда следует, что
Заметим,
что если 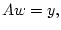 где
где
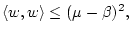
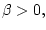 то
то
В этом случае
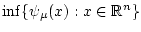 достигается.
Считая данное условие выполненным, представим
достигается.
Считая данное условие выполненным, представим 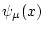 в
виде
в
виде
где
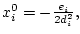
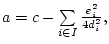 причем
причем 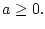
Приравнивая нулю производные 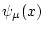 в точке минимума, получим
в точке минимума, получим
(в
предположении, что 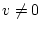 ), где обозначено
), где обозначено
Умножив каждое из равенств
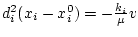 на
на
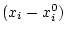 и сложив, получим
и сложив, получим
Следовательно,
и после подстановки
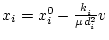 получим
получим
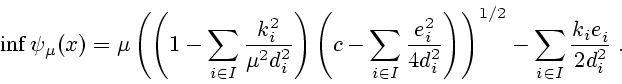 |
(3.5) |
Приведенные рассуждения справедливы, если в точке
минимума
Равенство нулю
возможно только при
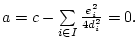
Если учесть, что
то в этом случае
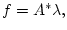 где
где
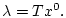 Тогда для любого
Тогда для любого 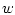
следовательно,
и мы снова приходим к формуле (3.5) .
Если условие
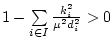 не выполнено, то
не выполнено, то
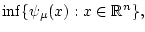 вообще говоря, не
достигается. В этом случае рассмотрим функцию
вообще говоря, не
достигается. В этом случае рассмотрим функцию
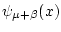 при
при 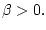 Для произвольного
Для произвольного 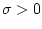 выберем
выберем 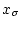 так, что
так, что
При достаточно малом 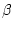
Отсюда
то есть
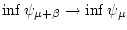 при
при
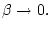 Выписывая для
Выписывая для
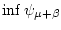 формулу (3.5) и переходя
к пределу при
формулу (3.5) и переходя
к пределу при
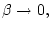 получим, что (3.5) дает величину
получим, что (3.5) дает величину
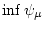 и в том случае, когда нижняя грань не достигается.
и в том случае, когда нижняя грань не достигается.
Обратимся к формуле для
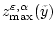 . Минимизируемая функция
имеет вид
. Минимизируемая функция
имеет вид
где
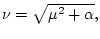
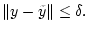
Представим
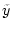 в виде
в виде
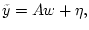 где
где
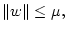
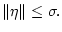 Тогда
Тогда
После замены 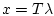 получим
получим
для любого
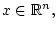 следовательно,
следовательно,
Если
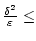
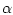 , то
, то
причем при
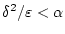 неравенство строгое.
неравенство строгое.
Таким образом, нижняя грань
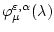 при
при
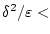
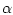 достигается. Проводя
далее рассуждения, аналогичные приведенным выше, получим
достигается. Проводя
далее рассуждения, аналогичные приведенным выше, получим
Обозначим
тогда
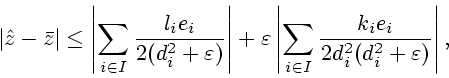 |
(3.6) |
где 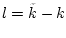 .
Учитывая, что
.
Учитывая, что
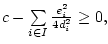 получим
получим
где
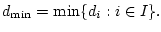 Из последних неравенств и
неравенства (3.6) получаем
Из последних неравенств и
неравенства (3.6) получаем
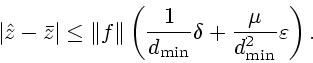 |
(3.7) |
Обозначим
Тогда
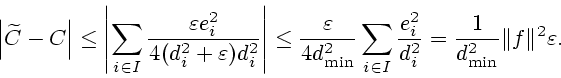 |
(3.8) |
Разность
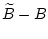 представим в виде
представим в виде
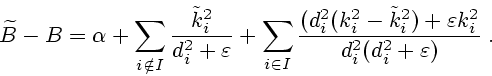 |
(3.9) |
Так как
то
Третье слагаемое в (3.9)
оценим сверху следующим образом, учитывая, что
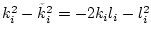 ,
,
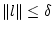 ,
, 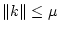
Таким образом, при
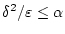
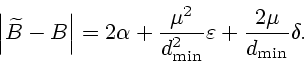 |
(3.10) |
Из (3.8), (3.10) следует
где
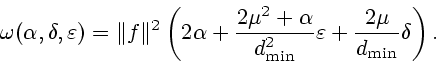 |
(3.11) |
Окончательно получаем следующее утверждение.
Теорема 3
Пусть пространство 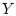 конечномерно.
Пусть
конечномерно.
Пусть
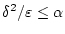 ,
,
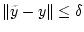 . Тогда
. Тогда
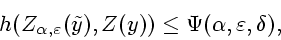 |
(3.12) |
где
Обозначим
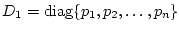 , где
, где
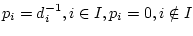 . При
. При 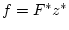 получим
получим
где
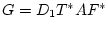 . Таким образом,
. Таким образом,
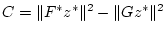 .
Аналог условия (2.12) принимает здесь следующий вид
.
Аналог условия (2.12) принимает здесь следующий вид
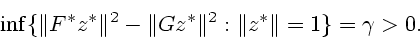 |
(3.13) |
При выполнении условия (3.13) и неравенства 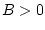 функцию
функцию
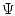 в (3.12) можно выбрать в следующем виде
в (3.12) можно выбрать в следующем виде


Next: 4 Случай оператора, заданного
Up: GUSEV
Previous: 2 Бесконечномерные наблюдения
2003-08-11
![]() ,
, ![]() обозначает
скалярное произведение в
обозначает
скалярное произведение в ![]() ,
,
![]() .
Величины
.
Величины
![]() из
решения двойственных экстремальных задач. Из теоремы
двойственности для задач выпуклого программирования [13]
следует, что
из
решения двойственных экстремальных задач. Из теоремы
двойственности для задач выпуклого программирования [13]
следует, что
![]() в следующем виде:
в следующем виде:
![]()
![]() ,
имеем
,
имеем
![]() Из условия
Из условия
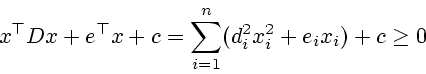
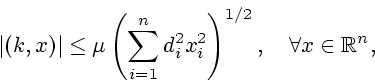
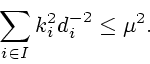
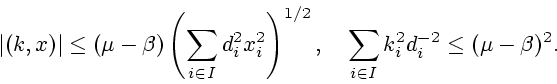
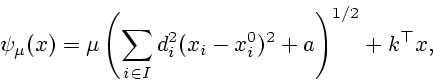
![]() в точке минимума, получим
в точке минимума, получим
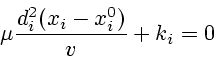
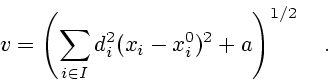
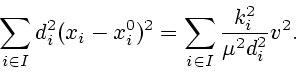
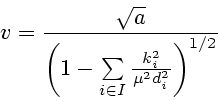
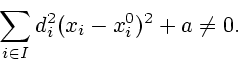
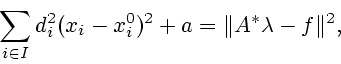
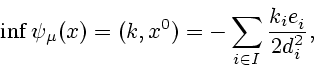
![]() не выполнено, то
не выполнено, то
![]() вообще говоря, не
достигается. В этом случае рассмотрим функцию
вообще говоря, не
достигается. В этом случае рассмотрим функцию
![]() при
при ![]() Для произвольного
Для произвольного ![]() выберем
выберем ![]() так, что
так, что
![]() . Минимизируемая функция
имеет вид
. Минимизируемая функция
имеет вид
![]() в виде
в виде
![]() где
где
![]()
![]() Тогда
Тогда
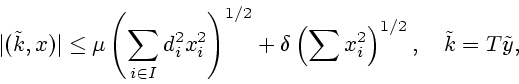
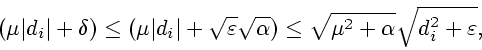
![]() при
при
![]()
![]() достигается. Проводя
далее рассуждения, аналогичные приведенным выше, получим
достигается. Проводя
далее рассуждения, аналогичные приведенным выше, получим
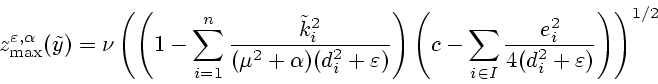
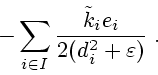
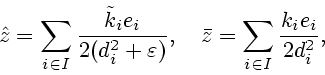
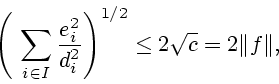
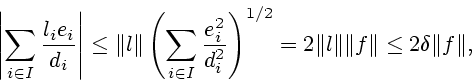
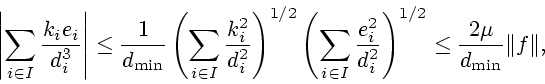
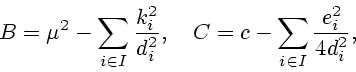
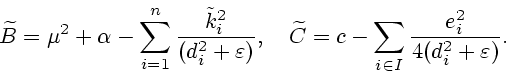
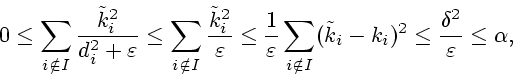
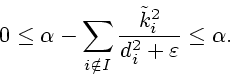
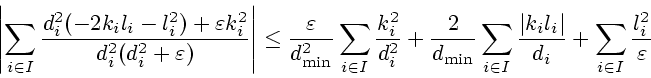
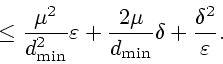
![]() , где
, где
![]() . При
. При ![]() получим
получим