6. Окрестностная реализация множеств притяжения

В предыдущем разделе обсуждалось представление МП, играющих роль регуляризаций обычного ДМ, в терминах ДМ некоторой (обобщенной) стандартной задачи. Решение последней, т.е. ${{\omega}^1}({g^{-1}}({\bf Y})),$ определяло при некоторых условиях требуемые МП в ТП $({\bf H},{{\tau}^{(2)}}),$ т.е. множества, получаемые "в пределе". С практической точки зрения интересно осуществить приближенную реализацию ${{\omega}^1}({g^{-1}}({\bf Y}))$ в виде ДМ соответствующего аналога "обычной" задачи с конкретным ослаблением ${\bf Y}$-ограничения. Мы будем именовать такую реализацию множества ${{\omega}^1}({g^{-1}}({\bf Y}))$ окрестностной. Так, в случае, когда версии ослабления ${\bf Y}$-ограничения допускают возможность произвольного выбора ${\bf G} \in {\cal Y}$ с последующей заменой ${\bf Y}$-ограничения условием ${s(f)} \in {\bf G},$ нас будет интересовать вопрос: когда по любой окрестности ${\tilde {\bf G}} \in {{\Bbb N}_{{\tau}^{(2)}}}[{{\omega}^1}({g^{-1}}({\bf Y}))]$ можно подобрать ${\bf G} \in {\cal Y}$ с соблюдением условия ${{\omega}^1}({g^{-1}}({\bf Y})) \subset \mathrm{cl}({h^1}({s^{-1}}({\bf G})), \tau^{(2)}) \subset {\tilde {\bf G}}.$ Соответствующие весьма прозрачные достаточные условия, рассматриваемые ниже, связаны со свойствами типа следствия 3.1.5 [22, стр. 197]. Мы, по сути дела, ограничиваемся далее сводкой достаточно простых предложений, опуская, как правило, очевидные доказательства. Сначала будут приведены некоторые общие "блоки" основной конструкции и лишь затем будет дана схема их применений к исследованию асимптотической версии задачи раздела 2.

В качестве непосредственного следствия положений [22, стр. 197] отметим свойство: если $U$ - непустое множество с оснащением ${\cal U} \in {{\cal B}[U]},\; (V,\tau),\linebreak V \ne \emptyset,$ есть ТП, $\varphi \in {V^U}$ и $\{H \in {\cal U} \mid {\mathrm{cl}}({{\varphi }^1}(H),\tau) \in (\tau \textrm{-} {\mathrm{comp}})[V]\} \ne \emptyset,$ то $\forall\,{G} \in \tau:$

$$((\tau \textrm{-} {\mathrm{LIM}})[{\cal U} \mid \varphi ] \s... ...n {\cal U}:\;{\mathrm{cl}}({{\varphi }^1}(M),\tau) \subset G).$$

Из данного утверждения в качестве следствия получаем очевидное

Предложение 6.1   Пусть $U$ - непустое множество с оснащением ${\cal U} \in {{\cal B}[U]};\; (V,\tau),\;V \ne \emptyset,$ есть ТП; $\varphi \in {V^U}.$ Пусть, кроме того, $\exists{H} \in {\cal U}:\;{\mathrm{cl}}({{\varphi }^1}(H),\tau) \in (\tau \textrm{-} {\mathrm{comp}})[V].$ Тогда

$$\begin{array}{c} \left({{\Bbb N}_{\tau}^0}[(\tau \textrm{-} ... ...au}[{\mathrm{cl}}({{\varphi }^1}(M), \tau)]\right). \end{array}$$

Следствие. Пусть $\;U$ - непустое множество с оснащением ${\cal U} \in {{\cal B}[U]}$; $(V,{{\tau}_1})$, $V \ne \emptyset ,$ - компактное ТП; $(W,\tau_2)$, $W \not= \emptyset$, - хаусдорфово ТП; $\alpha \in {V^U};\; \beta \in C(V,{{\tau}_1},W,{{\tau}_2});\;S \in {{\Bbb N}_{{... ..._2}}[({{\tau}_2} \textrm{-} {\mathrm{LIM}})[{\cal U} \mid \beta \circ \alpha]].$ Тогда

$$\exists{P} \in {\cal U}\;\forall\,{Q} \in {\cal U}:\;(Q \sub... ...}_2}}[{\mathrm{cl}}({(\beta \circ \alpha)^1}(Q),{{\tau}_2})]).$$ (6.1)

Заметим, что (6.1) можно рассматривать, как реализацию МП с точностью до любой наперед выбранной окрестности. В части обоснования (6.1) отметим только, что (в условиях следствия) $\beta$ есть замкнутое, в смысле ${\tau}_1$ и ${\tau}_2,$ отображение, а тогда при $H \in {\cal U}$ имеем

$${\mathrm{cl}}({(\beta \circ \alpha)^1}(H),{{\tau}_2}) = {\ma... ...),{{\tau}_1})) \in ({{\tau}_2} \textrm{-} {\mathrm{comp}})[W].$$

Дальнейшее рассуждение очевидно. Установленное следствие есть развитие теоремы 2.5.2 [6, стр. 41].

Отметим сейчас некоторые аналоги предложения 6.1 (и его следствия), связанные с использованием счетно-компактных ТП. Сначала сделаем
несколько совсем простых наблюдений.

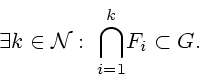Предложение 6.2   Пусть $(X,\tau)$ - счетно-компактное ТП, $(F_i)_{i \in {\cal N}}$ - последовательность в ${{\cal F}_\tau}$ и $G \in \tau.$ Если пересечение всех множеств ${F_i},\;i \in {\cal N},$ содержится в множестве $G,$ то

$$\exists{k} \in {\cal N}:\;{\bigcap\limits_{i=1}^k}{F_i} \subset G.$$ (6.2)

Доказательство аналогично рассуждению по обоснованию следствия 3.1.5 [22] (в частном случае последнего). Теперь вполне очевидно

Следствие. Пусть $(X,\tau)$ - ТП, $(F_i)_{i \in {\cal N}}$ - последовательность в ${{\cal F}_\tau}$, $G \in \tau.$ Пусть, кроме того, для некоторого $p \in {\cal N}$ множество $F_p$ счетно-компактно в ТП $(X,\tau).$ Пусть, наконец, пересечение всех множеств ${F_i}$, $i \in {\cal N},$ есть подмножество $G.$ Тогда справедливо (6.2).

Предложение 6.3   Пусть $(X,\tau)$ есть ТП, ${\cal X} \in {{\cal B}_{\cal N}}(X) \cap {{\cal P}({\cal F}_\tau)},\;G \in \tau.$ Пусть, кроме того, семейство ${\cal X}$ содержит некоторое счетно-компактное в ТП $(X,\tau)$ множество $F \in {\cal X}.$ Пусть, наконец, пересечение всех множеств из ${\cal X}$ есть подмножество $G.$ Тогда $\exists{H} \in {\cal X}:\; H \subset G.$

Доказательство легко получается комбинацией предыдущих положений настоящего раздела и конструкций заключительной части [10]. Вполне очевидно следующее

Предложение 6.4   Пусть $U$ - непустое множество с оснащением ${\cal U} \in {{\cal B}_{\cal N}}(U),\;(V,\tau)$ - ТП и $f \in {V^U}.$ Тогда

$$\{{\mathrm{cl}}({f^1}(H),\tau):\;H \in {\cal U}\} \in {{\cal B}_{\cal N}}(V) \cap {{\cal P}({\cal F}_\tau)}.$$ (6.3)

Семейство (6.3) может использоваться в качестве семейства ${\cal X}$ предложения 6.3.

Предложение 6.5   Пусть $U$ - непустое множество с оснащением ${\cal U} \in {{\cal B}_{\cal N}}(U);\;(V,\tau),\;V \ne \emptyset,$ есть ТП, $\varphi \in {V^U}.$ Пусть, кроме того, существует множество $H \in {\cal U},$ для которого ${\mathrm{cl}}({{\varphi }^1}(H),\tau)$ есть счетно-компактное множество в ТП $(V,\tau).$ Тогда $\forall\,{G} \in \tau:$

$$((\tau \textrm{-} {\mathrm{LIM}})[{\cal U} \mid \varphi ] \s... ...n {\cal U}:\;{\mathrm{cl}}({{\varphi }^1}(M),\tau) \subset G).$$

Доказательство сводится к комбинации двух предыдущих утверждений.

Предложение 6.6   Пусть $(U,{\cal U}),\;(V,\tau),\;\varphi$ удовлетворяют всем условиям предложения 6.5, включая требование счетной компактности в ТП $(V,\tau)$ множества ${\mathrm{cl}}({{\varphi }^1}(H),\tau)$ при некотором $H \in {\cal U}.$ Тогда

$$\begin{array}{c} \left({{\Bbb N}_\tau^0}[(\tau \textrm{-} {\... ...au}[{\mathrm{cl}}({{\varphi }^1}(M), \tau)]\right). \end{array}$$

Доказательство следует из определений раздела 3 и предложения 6.5.

Предложение 6.7   Пусть $U$ - непустое множество с оснащением ${\cal U} \in {{\cal B}_{\cal N}}(U);\;(V,{{\tau}_1}),\;V \ne \emptyset,$ - счетно-компактное ТП; $(W,{{\tau}_2}),\;W \ne \emptyset,$ - произвольное ТП; $\alpha \in {V^U};\;\beta$ - замкнутое, в смысле $(V,{{\tau}_1})$ и $(W,{{\tau}_2}),$ отображение из $V$ в $W;\;S \in {{\Bbb N}_{{\tau}_2}}[({{\tau}_2} \textrm{-} {\mathrm{LIM}})[{\cal U} \mid \beta \circ \alpha]].$ Тогда справедливо (6.1).

Д о к а з а т е л ь с т в о. Если $H \in {\cal U},$ то в силу замкнутости $\beta$ имеем

$${\mathrm{cl}}({(\beta \circ \alpha)^1}(H),{{\tau}_2}) = {\ma... ...m{cl}}({{\alpha}^1}(H),{{\tau}_1})) \in {{\cal F}_{{\tau}_2}}.$$ (6.4)

При этом ${\mathrm{cl}}({{\alpha}^1}(H),{{\tau}_1}) \in {{\cal F}_{{\tau}_1}}$ и, в силу счетной компактности $(V,{{\tau}_1}),$ множество ${\mathrm{cl}}({{\alpha}^1}(H),{{\tau}_1})$ счетно-компактно в данном ТП $(V,{{\tau}_1}).$ Поскольку, в частности, $\beta \in C(V,{{\tau}_1},W,{{\tau}_2}),$ то ${{\beta}^1}({\mathrm{cl}}({{\alpha}^1}(H),{{\tau}_1}))$ есть множество, счетно-компактное в ТП $(W,{{\tau}_2});$ упомянутые свойства см., например, в [22, стр. 305]. Стало быть, каждое множество (6.4), где $H \in {\cal U},$ счетно-компактно в ТП $(W,{{\tau}_2}).$ Итак, непустое множество $U$ оснащено семейством ${\cal U} \in {{\cal B}_{\cal N}}(U)$, $(W,{{\tau}_2})$ есть ТП ( $W \ne \emptyset),\;\beta \circ \alpha \in {W^U}$ и существует (поскольку ${\cal U} \ne \emptyset$) множество $H \in {\cal U},$ для которого множество (6.4) счетно-компактно в ТП $(W,{{\tau}_2}).$ Тогда согласно предложению 6.6

$${{\Bbb N}_{{\tau}_2}}[({{\tau}_2} \textrm{-} {\mathrm{LIM}})... ...2}}[{\mathrm{cl}}({{(\beta \circ \alpha)}^1}(M), {{\tau}_2})].$$

Итак, $S \in {{\Bbb N}_{{\tau}_2}}[{\mathrm{cl}}({{(\beta \circ \alpha)}^1}(P), {{\tau}_2})]$ при некотором $P \in {\cal U}.$ Если же $Q \in {\cal U}$ и $Q \subset P,$ то ${\mathrm{cl}}({{(\beta \circ \alpha)}^1}(Q)$, ${{\tau}_2})$ $\subset {\mathrm{cl}}({{(\beta \circ \alpha)}^1}(P),{{\tau}_2})$ и, тем более, $S \in {{\Bbb N}_{{\tau}_2}}[{\mathrm{cl}}({{(\beta \circ \alpha)}^1}(Q), {{\tau}_2})]$. $\Box$

З а м е ч а н и е 6.1. В формулировке предложения 6.7 предположение о счетной компактности ТП $(V,{{\tau}_1})$ можно заменить, не нарушая доказываемого утверждения, предположением о секвенциальной компактности данного ТП, поскольку в последнем случае реализуется частный случай [22, стр. 314] вышеупомянутого предложения 6.7.

Вернемся к рассмотрению конструкций раздела 5, оперируя с моделью (5.2), (5.3). Нас будут интересовать здесь вопросы уточнения представлений МП в виде ${{\omega}^1}({g^{-1}}({\bf Y})),$ исследуемые на основе утверждений настоящего раздела: мы возвращаемся к проблеме окрестностной реализации множества ${{\omega}^1}({g^{-1}}({\bf Y}))$ в том смысле, как это было сформулировано в начале раздела.

Теорема 6.1   Пусть выполнено условие 5.1, $({\bf K},{{\tau}^{(3)}})$ есть компактное ТП, а $({\bf H},{{\tau}^{(2)}})$ - хаусдорфово ТП. Тогда $\forall\,{S} \in {{\Bbb N}_{{\tau}^{(2)}}}[{{\omega}^1}({g^{-1}}({\bf Y}))]\; \exists{P} \in {\cal Y}\;\forall\,{\Bbb Q} \in {\cal Y}:$

$$({\Bbb Q} \subset P) \Longrightarrow (S \in {{\Bbb N}_{{\tau... ...}}[{\mathrm{cl}}({h^1}({s^{-1}}({\Bbb Q})), {{\tau}^{(2)}})]).$$

П р и м е ч а н и е. Заметим, что в рассматриваемом случае согласно теореме 5.1 имеет место совпадение множеств ${{\omega}^1}({g^{-1}}({\bf Y}))$ и $({{\tau}^{(2)}} \textrm{-} {\mathrm{LIM}})[{s^{-1}}[{\cal Y}] \mid h],$ ибо $\omega$ есть почти совершенное отображение в условиях данной теоремы. Упомянутое обстоятельство означает, в частности, что в случае, рассматриваемом в теореме 6.1, имеет место

$$\forall\,{\Bbb Q} \in {\cal Y}:\;{{\omega}^1}({g^{-1}}({\bf ... ...ubset {\mathrm{cl}}({h^1}({s^{-1}}({\Bbb Q})),{{\tau}^{(2)}}).$$

Поэтому теорема 6.1 говорит о возможности "сколь угодно точной"
реализации ${{\omega}^1}({g^{-1}}({\bf Y}))$ в виде ${\mathrm{cl}}({h^1}({s^{-1}}({\Bbb Q})),{{\tau}^{(2)}})$ при ослаблении
${\bf Y}$-ограничения $s(f) \in {\bf Y}$ до аналогичного ${\Bbb Q}$-ограничения.

Д о к а з а т е л ь с т в о теоремы 6.1. В силу теоремы 5.1 имеем, как уже отмечалось в примечании, равенство ${{\omega}^1}({g^{-1}}({\bf Y})) = ({{\tau}^{(2)}} \textrm{-} {\mathrm{LIM}})[{s^{-1}}[{\cal Y}] \mid h].$ Воспользуемся следствием предложения 6.1 при следующей конкретизации его параметров: $U = {\bf F},\;{\cal U} = {s^{-1}}[{\cal Y}],\;(V,{{\tau}_1}) = ({\bf K},{{\tau}... ...}}),\;(W,{{\tau}_2}) = ({\bf H},{{\tau}^{(2)}}),\; \alpha = m,\;\beta = \omega.$ Если $S \in {{\Bbb N}_{{\tau}^{(2)}}}[{{\omega}^1}({g^{-1}}({\bf Y}))],$ то в силу (6.1) можно указать ${\tilde P} \in {s^{-1}}[{\cal Y}]$ такое, что при ${\tilde Q} \in {s^{-1}}[{\cal Y}],$ $\tilde Q \subset \tilde P$, имеет место (см.(5.3)) $S \in {{\Bbb N}_{{\tau}^{(2)}}}[{\mathrm{cl}}({h^1}({\tilde Q}), {{\tau}^{(2)}})].$ Подбирая $P \in {\cal Y}$ так, что ${\tilde P} = {s^{-1}}(P),$ мы получаем утверждение теоремы.

В части использования, в качестве $({\bf K},{{\tau}^{(3)}}),$ счетно-компактного ТП будем, как и в предложениях 5.7, 5.8, ориентироваться на реализацию, в качестве запаса "допустимых" (при ослаблении ${\bf Y}$-ограничения) окрестностей, семейства ${\mathfrak Y}$ (5.12). Как уже отмечалось в замечании 5.3, в ряде практически интересных случаев семейство (5.12) имеет счетную базу.

Теорема 6.2   Пусть выполнено условие 5.2 и ${\mathfrak Y} \in {{\cal B}_{\cal N}}({\bf X}).$ Кроме того, пусть $({\bf K},{{\tau}^{(3)}})$ есть счетно-компактное ТП, а $({\bf H},{{\tau}^{(2)}})$ есть
${T_1}$-пространство. Пусть, наконец, $\omega$ есть замкнутое, в смысле ТП
$({\bf K},{{\tau}^{(3)}})$ и $({\bf H},{{\tau}^{(2)}})$, отображение из ${\bf K}$ в ${\bf H}.$ Тогда $\forall\,{S} \in {{\Bbb N}_{{\tau}^{(2)}}}[{{\omega}^1}({g^{-1}}({\bf Y}))]$ $\exists{P} \in {\mathfrak Y}\;\forall\,{\Bbb Q} \in {\mathfrak Y}:$

$$({\Bbb Q} \subset P) \Longrightarrow (S \in {{\Bbb N}_{{\tau... ...}}[{\mathrm{cl}}({h^1}({s^{-1}}({\Bbb Q})), {{\tau}^{(2)}})]).$$

Д о к а з а т е л ь с т в о. В силу предложения 5.7 имеем равенство (5.13). Рассмотрим предложение 6.7 в следующей его конкретизации: $U = {\bf F},\;{\cal U} = {s^{-1}}[{\mathfrak Y}],\;(V,{{\tau}_1}) = ({\bf K},{{... ...}}),\;(W,{{\tau}_2}) = ({\bf H},{{\tau}^{(2)}}),\; \alpha = m,\;\beta = \omega.$ Фиксируем $S \in {{\Bbb N}_{{\tau}^{(2)}}}[{{\omega}^1}({g^{-1}}({\bf Y}))].$ С учетом (5.3), (5.13), (6.1) и предложения 6.7 получаем, что можно указать ${\tilde P} \in {s^{-1}}[{\mathfrak Y}]$ такое, что

$$\forall\,{\tilde Q} \in {s^{-1}}[{\mathfrak Y}]:\;({\tilde Q... ...au}^{(2)}}}[{\mathrm{cl}}({h^1}({\tilde Q}),{{\tau}^{(2)}})]).$$ (6.5)

Мы учитываем здесь, что ${s^{-1}}[{\mathfrak Y}] \in {{\cal B}_{\cal N}}({\bf F}).$ Пусть $P \in {\mathfrak Y}$ таково, что ${\tilde P} = {s^{-1}}(P).$ Если ${\Bbb Q} \in {\mathfrak Y}$ и при этом ${\Bbb Q} \subset P,$ то импликация (6.5) истинна при ${\tilde Q} = {s^{-1}}({\Bbb Q}).$ Поскольку выбор $S$ был произвольным, предложение доказано.$\Box$

Теорему 6.2 полезно дополнить свойством, подобным обсуждавшемуся в примечании к теореме 6.1. Дело в том, что согласно предложению 5.7 и определениям раздела 3 в условиях теоремы 6.2 имеет место $\forall\,{\Bbb Q} \in {\mathfrak Y}:\;{{\omega}^1}({g^{-1}}({\bf Y})) \subset {\mathrm{cl}}({h^1}({s^{-1}}({\Bbb Q})),{{\tau}^{(2)}}).$