Конструкции предыдущих разделов могут быть дополнены
целым рядом весьма очевидных следствий и естественных аналогов. Мы
ограничимся сейчас кратким обсуждением лишь одной возможности,
связанной с исследованием универсальности МП по отношению к
топологии
![]() (см. раздел 2) пространства, в котором
"регистрируется" нарушение ограничений. В этой связи вернемся к
следствию 3.1,
чтобы отметить полезное
(см. раздел 2) пространства, в котором
"регистрируется" нарушение ограничений. В этой связи вернемся к
следствию 3.1,
чтобы отметить полезное
| (7.1) |
Д о к а з а т е л ь с т в о. Из предположений следует, в частности, что
![]() Из следствия 3.1 имеем
совпадение множеств
Из следствия 3.1 имеем
совпадение множеств
![]() и
и
![]() ;
для обоснования достаточно в упомянутом следствии заменить ТП
;
для обоснования достаточно в упомянутом следствии заменить ТП
![]() на
на
![]() C другой стороны, имеем при
C другой стороны, имеем при ![]() вложение
вложение
![]() и, как
следствие,
и, как
следствие,
![]() Кроме того,
Кроме того,
![]() и, как следствие,
и, как следствие,
![]() Из (3.11) имеем теперь
Из (3.11) имеем теперь
Данное утверждение имеет смысл связать с конструкцией окрестностнозначных отображений.
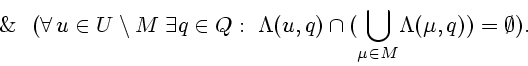 |
(7.2) |
![\begin{displaymath}
\begin{array}{c}
{{\bf g}^{-1}}(M) = ({{\tau}_3} \textrm{-}
...
...alpha}^{-1}}[{{\Bbb N}_{{\tau}_2}}[M]] \mid \beta].
\end{array}\end{displaymath}](img659.gif)
Д о к а з а т е л ь с т в о. Из определений раздела 3 имеем
![]() Кроме того, имеем
Кроме того, имеем
![]() а тогда
а тогда
![]()
![\begin{displaymath}
{\bigcup\limits_{\mu \in M}}{\Lambda }(\mu,q) \in {{\Bbb N}_{{\tau}_1}}[M].
\end{displaymath}](img663.gif)
| (7.3) |
| (7.4) |
На основе предложений 7.1 и 7.2 можно построить конкретизации,
допускающие применение к исследованию основной задачи
данного раздела по рецептам раздела 5. Мы ограничимся лишь
несколькими наблюдениями, имеющими своей целью
построение более универсальных, в отношении способа ослабления
![]() -ограничения, МП. Вернемся к задаче раздела 2, где первоначально
были фиксированы лишь непустые множества
-ограничения, МП. Вернемся к задаче раздела 2, где первоначально
были фиксированы лишь непустые множества
![]() и
и ![]() операторы
операторы
![]() и
и
![]() а также множество
а также множество
![]() что вполне достаточно для постановки, ориентированной на определение
что вполне достаточно для постановки, ориентированной на определение
![]() При переходе к асимптотической версии данной постановки множество
При переходе к асимптотической версии данной постановки множество
![]() было оснащено топологией
было оснащено топологией
![]() в определенной
степени ``стандартно", в то время
как оснащение
в определенной
степени ``стандартно", в то время
как оснащение ![]() весьма неочевидно (см. раздел 2). Принимая
в качестве естественного вариант ослабления
весьма неочевидно (см. раздел 2). Принимая
в качестве естественного вариант ослабления ![]() -ограничения
путем использования окрестностей множества
-ограничения
путем использования окрестностей множества ![]() вместо самого
вместо самого
![]() логично ориентироваться на некоторый набор возможных
топологий
логично ориентироваться на некоторый набор возможных
топологий ![]() и стремиться при этом к
универсальному, для данного набора,
МП в качестве регуляризации ДМ. В этой связи мы вместо
и стремиться при этом к
универсальному, для данного набора,
МП в качестве регуляризации ДМ. В этой связи мы вместо
![]() введем в рассмотрение две (сравнимых)
топологии
введем в рассмотрение две (сравнимых)
топологии
![]() и
и
![]() множества
множества ![]() для которых имеет место
для которых имеет место
![]() Соответственно,
полагаем
Соответственно,
полагаем
![\begin{displaymath}
({{\cal Y}_{\bf l}} \stackrel{\triangle}{=}{{\Bbb N}_{{\tau}...
...krel{\triangle}{=}{{\Bbb N}_{{\tau}_{\bf u}^{(1)}}}[{\bf Y}]).
\end{displaymath}](img680.gif) |
(7.5) |
З а м е ч а н и е 7.1. Предположение относительно функции ![]() означает в силу сравнимости
топологий
означает в силу сравнимости
топологий
![]() факт
"универсальной" непрерывности данной функции, поскольку
в рассматриваемом случае непременно имеет место свойство
факт
"универсальной" непрерывности данной функции, поскольку
в рассматриваемом случае непременно имеет место свойство
З а м е ч а н и е 7.2. В силу сравнимости двух вышеупомянутых топологий множества ![]() имеем следующее свойство. Если имеет место
имеем следующее свойство. Если имеет место
| (7.6) |
| (7.7) |
З а м е ч а н и е 7.3. Допустим, что заданы непустое множество ![]() и
и
некоторое (окрестностнозначное)
отображение
![]() (т.е. реализуется вариант соглашения раздела 5 при
(т.е. реализуется вариант соглашения раздела 5 при
![]() ). Разумеется,
). Разумеется,
![]() Как следствие,
Как следствие,
![]() С учетом (3.5) имеем, что
С учетом (3.5) имеем, что
Выводы. Результаты, полученные на основе использования модели,
которую характеризует кортеж
![]() определяют (при сравнительно необременительных условиях) в виде
определяют (при сравнительно необременительных условиях) в виде
![]() весьма универсальную, в смысле
варьирования способа ослабления
весьма универсальную, в смысле
варьирования способа ослабления ![]() -ограничения, регуляризацию
задачи о построении МДЭ и ДМ. В этом отношении показательны, в частности,
утверждения, реализуемые в виде положений раздела 5 с учетом замечаний
7.1-7.3 в терминах пары сравнимых топологий множества
-ограничения, регуляризацию
задачи о построении МДЭ и ДМ. В этом отношении показательны, в частности,
утверждения, реализуемые в виде положений раздела 5 с учетом замечаний
7.1-7.3 в терминах пары сравнимых топологий множества ![]() .
Предложения 7.1, 7.2 с учетом утверждений раздела 5 наглядно характеризуют
универсальную обобщенную задачу, реализующую "стандартное" ДМ
.
Предложения 7.1, 7.2 с учетом утверждений раздела 5 наглядно характеризуют
универсальную обобщенную задачу, реализующую "стандартное" ДМ
![]() В части характеризации диапазона
ограничений асимптотического характера отметим, что для сильнейшей из
двух вышеупомянутых топологий
В части характеризации диапазона
ограничений асимптотического характера отметим, что для сильнейшей из
двух вышеупомянутых топологий ![]() используется, для построения
ослабленных версий
используется, для построения
ослабленных версий ![]() -ограничения, семейство всех окрестностей
множества
-ограничения, семейство всех окрестностей
множества ![]() Тем самым реализуется семейство
Тем самым реализуется семейство
![]() элементы которого используются в качестве допустимых (к использованию
для целей "размывания"
элементы которого используются в качестве допустимых (к использованию
для целей "размывания" ![]() -ограничения) окрестностей. Тем самым
реализуется режим, наиболее приближенный к условиям невозмущенной задачи.
Для слабейшей из рассматриваемых топологий (т.е. для топологии
-ограничения) окрестностей. Тем самым
реализуется режим, наиболее приближенный к условиям невозмущенной задачи.
Для слабейшей из рассматриваемых топологий (т.е. для топологии
![]() ), напротив, целесообразно сокращение
семейства допустимых окрестностей до
), напротив, целесообразно сокращение
семейства допустимых окрестностей до ![]() (см. замечание 7.3).
Отметим, что конкретный вариант использования двух сравнимых топологий
(см. Замечания 7.1-7.3) рассматривался в [25] (см. также
[11,26]).
(см. замечание 7.3).
Отметим, что конкретный вариант использования двух сравнимых топологий
(см. Замечания 7.1-7.3) рассматривался в [25] (см. также
[11,26]).
Поступила 15.09.99