В последующих построениях будут использоваться общие свойства ТП как на уровне исходной постановки, где эти ТП являются параметрами задачи, так и на уровне моделей, подбираемых в интересах получения требуемых представлений для регуляризированных версий решения исходной задачи. По этой причине мы не фиксируем множества, оснащаемые топологиями, что предполагает известную аккуратность в формулировках. Последняя, в свою очередь, требует введения достаточно развитой системы обозначений и основных понятий.
Далее используются кванторы и логические связки, символы: ![]() (по
определению) и
(по
определению) и
![]() (равенство по определению). Семейство всех (всех непустых)
подмножеств множества
(равенство по определению). Семейство всех (всех непустых)
подмножеств множества ![]() обозначаем через
обозначаем через ![]() (через
(через ![]() ). Для
множества всех отображений из множества
). Для
множества всех отображений из множества ![]() в множество
в множество ![]() используем
традиционное [24, стр. 77] обозначение
используем
традиционное [24, стр. 77] обозначение ![]() ; в упомянутых условиях для
; в упомянутых условиях для
![]() и
и
![]() через
через ![]() (через
(через ![]() )
обозначаем сужение
)
обозначаем сужение ![]() на
на ![]() (образ множества
(образ множества ![]() при отображении
при отображении
![]() ); см., например, [19, стр. 26]. Через
); см., например, [19, стр. 26]. Через ![]() обозначаем множество
всех вещественных чисел,
обозначаем множество
всех вещественных чисел,
![]() есть натуральный ряд. Разумеется, если
есть натуральный ряд. Разумеется, если ![]() - множество, то
- множество, то
![]() есть множество всех последовательностей в
есть множество всех последовательностей в ![]() . В качестве
множеств в упомянутых определениях могут, конечно, использоваться
семейства (множеств); в частности, далее будут использоваться
множественнозначные отображения, т.е. отображения, значениями
которых являются множества.
Для пустого множества, одноэлементных множеств и
неупорядоченных пар используем традиционные обозначения
. В качестве
множеств в упомянутых определениях могут, конечно, использоваться
семейства (множеств); в частности, далее будут использоваться
множественнозначные отображения, т.е. отображения, значениями
которых являются множества.
Для пустого множества, одноэлементных множеств и
неупорядоченных пар используем традиционные обозначения ![]() ,
,
![]() ,
, ![]() ; в последнем случае не исключается возможность
; в последнем случае не исключается возможность ![]() .
.
Если ![]() - множество, то через
- множество, то через ![]() обозначаем множество всех
семейств
обозначаем множество всех
семейств
![]() таких, что
таких, что
![]()
![]()
![]() ; тогда
; тогда
![]() есть [20] множество
всех базисов фильтров
есть [20] множество
всех базисов фильтров ![]() . Наконец, в согласии с [7, стр. 37] полагаем,
что, для произвольного множества
. Наконец, в согласии с [7, стр. 37] полагаем,
что, для произвольного множества ![]() ,
,
![]() есть
есть ![]() множество всех семейств
множество всех семейств
![]() , для каждого из которых
, для каждого из которых
![]()
![]()
![]() ; семейства из
; семейства из
![]() интерпретируем, как элементы
интерпретируем, как элементы ![]() со счетной базой. Далее
используется стандартное определение фильтра (см., например,
[21, стр. 100], [22, стр. 91, 92]) в произвольном
множестве. В частности, если
со счетной базой. Далее
используется стандартное определение фильтра (см., например,
[21, стр. 100], [22, стр. 91, 92]) в произвольном
множестве. В частности, если
![]() есть направленность [19, гл. 2] в множестве
есть направленность [19, гл. 2] в множестве ![]() , т.е.
, т.е.
![]() есть непустое направленное множество (НМ)
[22, стр. 27] и
есть непустое направленное множество (НМ)
[22, стр. 27] и ![]() , то
, то
| (3.1) |
Если ![]() - непустое множество с оснащением
- непустое множество с оснащением
![]() ,
, ![]() есть ТП и
есть ТП и ![]() , то (см. [6, стр. 39, 40],
[7, стр. 35]) множество
, то (см. [6, стр. 39, 40],
[7, стр. 35]) множество
![]() , определяемое в виде пересечения всех множеств
, определяемое в виде пересечения всех множеств
![]() ,
,
![]() , есть одновременно множество всех
, есть одновременно множество всех
![]() , для каждого из которых можно указать такую направленность
, для каждого из которых можно указать такую направленность
![]() в
в ![]() , что
, что
| (3.2) |
Если
![]() есть ТП, то через
есть ТП, то через
![]() обозначаем семейство всех компактных [22, стр. 196] в
обозначаем семейство всех компактных [22, стр. 196] в
![]() подмножеств
подмножеств ![]() . В связи с общими свойствами
компактных множеств, определяемых в терминах подпространств исходного
ТП, см. [19]-[23]. Если
. В связи с общими свойствами
компактных множеств, определяемых в терминах подпространств исходного
ТП, см. [19]-[23]. Если ![]() и
и ![]() - непустые множества,
- непустые множества,
![]() - ТП и
- ТП и
![]() , то
, то
| (3.3) |
| (3.4) |
В дальнейшем часто используется следующая конкретизация семейств из
![]() , где
, где ![]() - множество. Если
- множество. Если ![]() и
и ![]() - множества,
- множества, ![]() и
и
![]() , то полагаем
, то полагаем
![]() ; если же
; если же
![]() , то
, то
![]() . В
частности (см. раздел 2), если
. В
частности (см. раздел 2), если ![]() - непустое множество,
- непустое множество, ![]() есть ТП,
есть ТП, ![]() и
и
![]() , то всегда
, то всегда
![]() ; вместо
; вместо
![]() может
использоваться то или иное семейство
может
использоваться то или иное семейство ![]() "характерных" окрестностей (например, в случае метризуемого ТП
"характерных" окрестностей (например, в случае метризуемого ТП ![]() обычно
используются
обычно
используются ![]() -окрестности
-окрестности ![]() ,
,
![]() ). Следуя в идейном
отношении [25], рассмотрим одну такую возможность. Если
). Следуя в идейном
отношении [25], рассмотрим одну такую возможность. Если
![]() ,
,
![]() , - ТП,
, - ТП, ![]() - непустое множество и
- непустое множество и
![]() , то полагаем, что
, то полагаем, что
![]() есть
есть ![]() множество всех
множество всех
![]() (т.е. множество всех
операторов, сопоставляющих каждой паре
(т.е. множество всех
операторов, сопоставляющих каждой паре
![]() , где
, где
![]() и
и
![]() , подмножество
, подмножество ![]() ) таких, что
) таких, что
![]()
![]() ; разумеется, при
; разумеется, при
![]() и
и ![]() имеем в виде объединения
всех множеств
имеем в виде объединения
всех множеств
![]() ,
, ![]() , элемент
семейства
, элемент
семейства
![]() (всех
(всех ![]() -окрестностей
-окрестностей ![]() ). Если
). Если
![]() ,
, ![]() и
и ![]() удовлетворяют условиям предыдущего определения,
удовлетворяют условиям предыдущего определения,
![]() и при всяком выборе
и при всяком выборе
![]() существует
существует ![]() , для которого
, для которого ![]() и объединение всех
множеств
и объединение всех
множеств
![]() ,
, ![]() , не пересекаются, то
, не пересекаются, то
![]() ; элементы
; элементы
![]() называем далее
окрестностнозначными отображениями. Уместно рассмотреть, в связи с
используемой конструкцией МП, несколько более узкий класс
окрестностнозначных отображений вышеупомянутого типа, привлекая идею
равномерных "уточнений" соответствующих окрестностей. Если
называем далее
окрестностнозначными отображениями. Уместно рассмотреть, в связи с
используемой конструкцией МП, несколько более узкий класс
окрестностнозначных отображений вышеупомянутого типа, привлекая идею
равномерных "уточнений" соответствующих окрестностей. Если ![]() ,
,
![]() , - ТП,
, - ТП, ![]() - непустое множество и
- непустое множество и
![]() , то через
, то через
![]() обозначаем множество всех
обозначаем множество всех
![]() таких, что
таких, что
| (3.5) |
![\begin{displaymath}
{\cal U}(Q, \tau, M \mid \tilde\Lambda ) \stackrel{\triangle...
...\mu \in
M} \tilde\Lambda (\mu,q): \ q \in Q\} \in {\cal B}[X].
\end{displaymath}](img148.gif) |
(3.6) |
Всюду в дальнейшем используем традиционное обозначение: если
![]() ,
,
![]() , и
, и ![]() ,
,
![]() , -
суть ТП, то
, -
суть ТП, то
![]() есть
есть ![]() множество всех
непрерывных, в смысле
множество всех
непрерывных, в смысле ![]() и
и ![]() , отображений из
множества
, отображений из
множества ![]() .
.
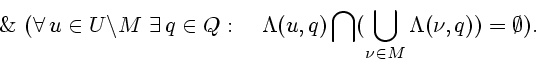 |
(3.7) |
Д о к а з а т е л ь с т в о. Используя (3.7), подберем
![]() со свойством
со свойством
![]() .
Пусть
.
Пусть
![]() . Используя (3.2), подберем для данной точки
. Используя (3.2), подберем для данной точки ![]() такую направленность
такую направленность
![]() в
в ![]() , что
, что
| (3.8) |
Доказательство аналогично предыдущему.
З а м е ч а н и е 3.1. Отметим совсем простой пример, мотивирующий специальное
исследование конструкций, ориентированных на установление факта
совпадения МП при использовании различных семейств окрестностей
множества ![]() (см. формулировки предложений 3.1, 3.2). Пусть
(см. формулировки предложений 3.1, 3.2). Пусть
![]() есть плоскость
есть плоскость ![]() в естественной топологии
покоординатной сходимости, а
в естественной топологии
покоординатной сходимости, а ![]() есть (замкнутое) множество всех
векторов
есть (замкнутое) множество всех
векторов
![]() таких, что
таких, что
![]() . Сравним семейство
. Сравним семейство
![]() всех окрестностей
всех окрестностей ![]() и семейство
и семейство ![]() всех открытых евклидовых
всех открытых евклидовых ![]() -окрестностей
-окрестностей ![]() (
(
![]() ). Легко видеть, что
). Легко видеть, что
![]() есть множество всех
есть множество всех
![]() со строго
положительными компонентами. Рассмотрим множество
со строго
положительными компонентами. Рассмотрим множество ![]() всех
всех
![]() таких, что
таких, что
![]() . Тогда
. Тогда
![]() обладает свойством: при всяком
обладает свойством: при всяком
![]() имеет место
имеет место
![]() . Итак, семейство
. Итак, семейство
![]() не образует фундаментальной системы окрестностей
не образует фундаментальной системы окрестностей ![]() . В
то же время
. В
то же время ![]() можно истолковать в виде (3.6) при надлежащем
выборе параметров. Действительно, достаточно полагать в (3.5), (3.6):
можно истолковать в виде (3.6) при надлежащем
выборе параметров. Действительно, достаточно полагать в (3.5), (3.6):
![]() , т.е.
, т.е.
![]() в топологии
покоординатной сходимости;
в топологии
покоординатной сходимости;
![]() . Кроме того, при
. Кроме того, при ![]() и
и ![]() предполагаем теперь, что
предполагаем теперь, что
![]() есть открытый круг
(эвклидов шар в
есть открытый круг
(эвклидов шар в ![]() ) с центром
) с центром ![]() и радиусом
и радиусом ![]() . При этих
условиях реализуется отображение
. При этих
условиях реализуется отображение
![]() и
и
![]() . Теперь имеет смысл
вернуться к предложению 3.1, что, в свою очередь, связано с проверкой
(3.7); нетривиальность самого утверждения данного предложения
мотивируется теперь "неэквивалентностью"
. Теперь имеет смысл
вернуться к предложению 3.1, что, в свою очередь, связано с проверкой
(3.7); нетривиальность самого утверждения данного предложения
мотивируется теперь "неэквивалентностью" ![]() и
и ![]() .
В связи с (3.7) отметим, что вторая часть условия (3.7), т.е. свойство
отделимости "с окрестностью" заданного типа, очевидным образом следует
при
.
В связи с (3.7) отметим, что вторая часть условия (3.7), т.е. свойство
отделимости "с окрестностью" заданного типа, очевидным образом следует
при
![]() из факта замкнутости
из факта замкнутости ![]() . Проверки, стало быть,
требует лишь первая часть (3.7), т.е. представимость
. Проверки, стало быть,
требует лишь первая часть (3.7), т.е. представимость ![]() в виде
"непрерывной суперпозиции". Представляется, что поиск представлений
такого типа является, по сути дела, одной из основных задач теории
расширений.
в виде
"непрерывной суперпозиции". Представляется, что поиск представлений
такого типа является, по сути дела, одной из основных задач теории
расширений.
Возвращаясь к анализу общих конструкций расширения пространств, отметим
| (3.9) |
Д о к а з а т е л ь с т в о. Пусть
![]() , т.е.
, т.е. ![]() обладает свойством
обладает свойством ![]() . Выберем произвольно
. Выберем произвольно
![]() , после чего подберем
, после чего подберем
![]() так, что при этом
так, что при этом
![]() .
Пусть
.
Пусть
![]() таково, что
таково, что
![]() .
Тогда
.
Тогда
![]() и, в силу непрерывности
оператора
и, в силу непрерывности
оператора ![]() , имеет место
, имеет место
![]() . Если
. Если
![]() , то
, то
![]() и, в силу свойства
и, в силу свойства
![]() , имеет место
, имеет место
| (3.10) |
| (3.11) |
Д о к а з а т е л ь с т в о. Для
![]() имеем
имеем
![]() , а потому
, а потому
![\begin{displaymath}= \bigcap_{H \in {\Bbb N}_{\tau_1}[M]} \mathrm{cl}(p^1((q \ci...
...{\tau_1}[M]} \mathrm{cl}(p^1(p^{-1}(q^{-1}(H))),\tau_2)
\subset\end{displaymath}](img256.gif)
![\begin{displaymath}
\subset \bigcap_{H \in {\Bbb N}_{\tau_1}[M]} \mathrm{cl}(q^{...
...ap_{H \in {\Bbb N}_{\tau_1}[M]} q^{-1}(\mathrm{cl}(H,\tau_1)).
\end{displaymath}](img257.gif) |
(3.12) |
Отметим, что условие (3.11) охватывает типичный для конструкций
расширения задач управления случай, когда ![]() есть замкнутое множество
в регулярном [19, стр. 154] ТП.
есть замкнутое множество
в регулярном [19, стр. 154] ТП.
Полезно отметить утверждение, получаемое соединением предложения 3.1 и следствия 3.1.
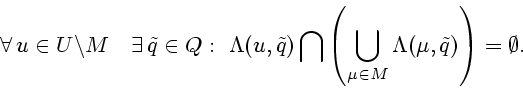 |
(3.13) |
| (3.14) |
Д о к а з а т е л ь с т в о. Из предложения 3.3 имеем вложение (3.9). Далее,
поскольку ![]() - окрестностнозначное отображение, то при
- окрестностнозначное отображение, то при ![]() и
и
![]() имеет место
имеет место
![]() . Кроме того, в силу
(3.6) имеем свойство
. Кроме того, в силу
(3.6) имеем свойство
![]() (мы учли здесь очевидное вложение
(мы учли здесь очевидное вложение
![]() ). В силу (3.6), (3.13) и
двух последних замечаний об окрестностях точек и множеств в ТП
). В силу (3.6), (3.13) и
двух последних замечаний об окрестностях точек и множеств в ТП
![]() мы получаем, что в рассматриваемом случае справедливо
(3.11). Поэтому выполнено утверждение следствия 3.1, т.е.
мы получаем, что в рассматриваемом случае справедливо
(3.11). Поэтому выполнено утверждение следствия 3.1, т.е.
| (3.15) |
Предложение 3.4 определяет общие условия весьма универсальной
реализации МП в виде решения стандартной задачи, или, короче, условия
"универсальной" стандартной реализации этих МП (см. в этой связи
замечание 3.1). Данные МП (см. предложения 3.1, 3.4 и следствие
предложения 3.3) объективно играют роль регуляризаций МДЭ исходной
задачи. Равенство (3.14) определяет структуру этой регуляризации
(напомним, что множество ![]() в условиях предложения 3.4 с
необходимостью замкнуто в
в условиях предложения 3.4 с
необходимостью замкнуто в ![]() ).
).
З а м е ч а н и е 3.2. Вернемся к предложению 3.3. Пусть ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() удовлетворяют всем условиям
предложения 3.3, включая плотность
удовлетворяют всем условиям
предложения 3.3, включая плотность ![]() в
в ![]() . Согласно
(3.9) любой элемент
. Согласно
(3.9) любой элемент ![]() допускает асимптотическую реализацию
посредством некоторого приближенного решения со свойствами, подобными
(3.2). Имеет смысл отметить одну простую возможность, фиксируя
допускает асимптотическую реализацию
посредством некоторого приближенного решения со свойствами, подобными
(3.2). Имеет смысл отметить одну простую возможность, фиксируя
![]() . Прежде всего
. Прежде всего
![]() , а потому
существует направленность
, а потому
существует направленность
![]() в
в ![]() , для которой
, для которой
![]() ; назовем каждую
направленность такого типа
; назовем каждую
направленность такого типа ![]() -аппроксимирующей (мы учли здесь
известную теорему Биркгофа [22, стр. 89]; см. также комментарий в
[22, стр. 96]). Оказывается, для асимптотической реализации
-аппроксимирующей (мы учли здесь
известную теорему Биркгофа [22, стр. 89]; см. также комментарий в
[22, стр. 96]). Оказывается, для асимптотической реализации ![]() в
смысле, подобном (3.2), можно использовать любую
в
смысле, подобном (3.2), можно использовать любую ![]() -аппроксимирующую
направленность. Действительно, пусть
-аппроксимирующую
направленность. Действительно, пусть
![]() есть
направленность в
есть
направленность в ![]() с вышеупомянутым свойством сходимости
с вышеупомянутым свойством сходимости
![]() к
к ![]() в ТП
в ТП ![]() (мы знаем уже, что
такая направленность существует). Покажем, что
(мы знаем уже, что
такая направленность существует). Покажем, что
| (3.16) |
| (3.17) |