Укажем необходимые условия на кривую ![]() реализующую
точную нижнюю грань (3) функционала
реализующую
точную нижнюю грань (3) функционала
Далее понадобятся следующие факты.
Пусть ![]() - нормированное пространство,
- нормированное пространство, ![]() Линейный
функционал
Линейный
функционал ![]() называется опорным в точке
называется опорным в точке ![]() если
если
- норма ![]() дифференцируема по Гато в точке
дифференцируема по Гато в точке ![]()
- отображение ![]() сильно-слабо непрерывно в точке
сильно-слабо непрерывно в точке
![]()
Обозначим
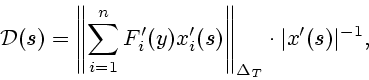
Д о к а з а т е л ь с т в о. Необходимым условием минимума функционала (6)
является справедливость неравенства
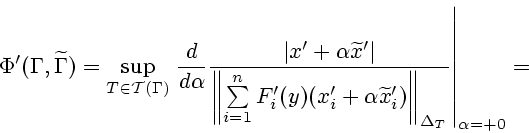
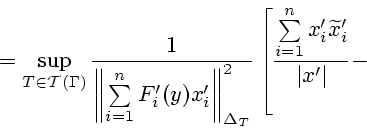
![\begin{displaymath}
\left.\left. -\vert x'\vert \frac{d}{d\alpha}
\frac{{\left...
...i'\right\Vert _{\Delta_T}}
\right\vert _{\alpha=+0} \right],
\end{displaymath}](img111.gif)
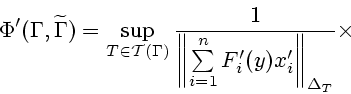
Необходимое условие (11) экстремальности траектории
![]() сводится к справедливости неравенства
сводится к справедливости неравенства
Следствие. Пусть
![]() есть норма
пространства
есть норма
пространства
![]() - дифференцируемая
вещественная функция и
- дифференцируемая
вещественная функция и
![]() Если
Если ![]() является решением задачи
является решением задачи ![]() то существует точка
то существует точка
![]() такая, что
такая, что
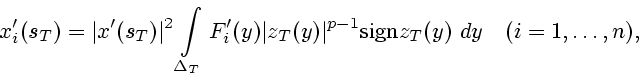
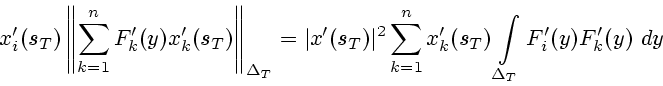
З а м е ч а н и е.
Теорема 3 дает основу итерационного алгоритма поиска оптимальной
траектории. Предположим, на некотором шаге найдена траектория
![]() не являющаяся оптимальной. Тогда не
существует точки
не являющаяся оптимальной. Тогда не
существует точки
![]() удовлетворяющей
соотношениям (10). Построим функции
удовлетворяющей
соотношениям (10). Построим функции
![]() обладающие свойствами (16), и в
соответствии с (17) определим
обладающие свойствами (16), и в
соответствии с (17) определим
![]() В силу (18), (13) и
компактности множества
В силу (18), (13) и
компактности множества
![]() выполняется
неравенство
выполняется
неравенство
![]() , а значит, при малых
, а значит, при малых
![]() получаем
получаем
![]()
Поступила 19.04.2000