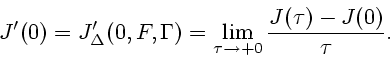

Next: 3 Производная модуля информативности
Up: berdyshev
Previous: 1 Введение
Рассмотрим класс 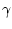 гладких кривых (траекторий)
гладких кривых (траекторий)
заданных посредством дифференцируемых вектор-функций
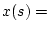
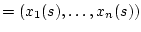 и соединяющих две фиксированные
точки
и соединяющих две фиксированные
точки
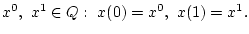 Возможность
решения задачи навигации определяется свойством информативности
геофизического поля вдоль траектории. Пусть для функций,
заданных на
Возможность
решения задачи навигации определяется свойством информативности
геофизического поля вдоль траектории. Пусть для функций,
заданных на
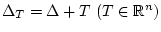 , определена
некоторая норма
, определена
некоторая норма
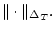 Свойство информативности
поля
Свойство информативности
поля 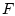 можно характеризовать посредством функции (см. [2])
можно характеризовать посредством функции (см. [2])
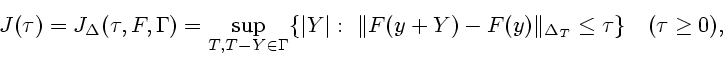 |
(1) |
где
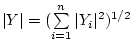 - евклидова длина вектора
- евклидова длина вектора
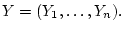 Функцию
Функцию 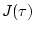 будем называть модулем
информативности поля на
будем называть модулем
информативности поля на 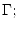 она показывает,
что
она показывает,
что
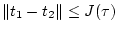 , если
, если
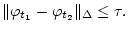
В случае, когда 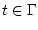 , задача навигации
сводится к следующей
, задача навигации
сводится к следующей
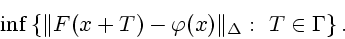 |
(2) |
Максимальная ошибка привязки, осуществленной посредством решения
задачи (2), есть
Пусть при решении задачи (2) найдена некоторая точка
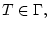 тогда по определению (1) будет
тогда по определению (1) будет
Эта оценка показывает, что важно знать поведение модуля
информативности в окрестности нуля, в частности, величину
производной
В данной работе приводятся необходимые условия на гладкую
траекторию, доставляющую нижнюю грань
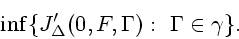 |
(3) |
2003-06-05
![]() гладких кривых (траекторий)
гладких кривых (траекторий)
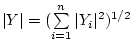 - евклидова длина вектора
- евклидова длина вектора
![]() , задача навигации
сводится к следующей
, задача навигации
сводится к следующей