В дальнейшем будем предполагать, что
- норма
![]() непрерывна по
непрерывна по ![]()
- функция ![]() скалярная, дифференцируемая и ее частные производные
скалярная, дифференцируемая и ее частные производные
![]() имеют равномерно ограниченную по
имеют равномерно ограниченную по
![]() норму
норму
![]()
- ![]() при
при ![]() и, значит, ввиду компактности
и, значит, ввиду компактности
![]() непрерывности функции
непрерывности функции ![]() и нормы
и нормы
![]() будет
будет ![]()
Для ![]() найдутся
найдутся
![]() экстремальные для (1), т.е.
экстремальные для (1), т.е.
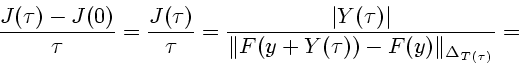
![\begin{displaymath}
J'(0)=\left[ \inf_{T\in \Gamma} \left\Vert
\lim_{{T+Y\in \...
...+Y)-F(y)}{\vert Y\vert}\right\Vert _{\Delta_T}\right]^
{-1}.
\end{displaymath}](img54.gif)
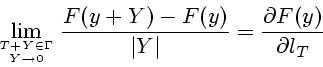
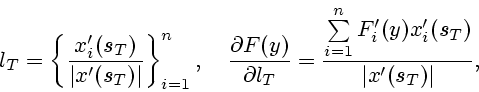
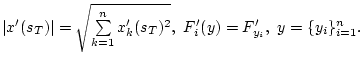 Итак,
Итак,