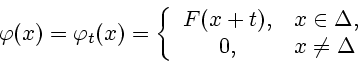

Next: 2 Постановка задачи о
Up: berdyshev
Previous: berdyshev
Пусть  - связная компактная область из
- связная компактная область из
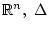 - множество из
- множество из 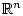 (множество визирования),
(множество визирования), 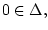 на
на 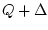 задана вектор-функция
задана вектор-функция 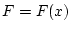 (геофизическое поле),
(геофизическое поле), 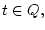
- фрагмент поля 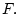 Задачей навигации по геофизическому полю
называют (см. [1]) задачу поиска точки
Задачей навигации по геофизическому полю
называют (см. [1]) задачу поиска точки 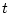 по известным наборам
значений
по известным наборам
значений 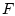 на
на 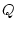 и фрагмента
и фрагмента 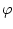 на
на 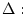
Эта задача вызвана проблемой определения местоположения
автономно двигающегося аппарата с использованием замеренного
фрагмента поля и информации о поле в целом. Компонентами поля
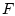 могут быть высота, оптическая яркость, радиояркость рельефа
и др.
могут быть высота, оптическая яркость, радиояркость рельефа
и др.
2003-06-05
![]() - связная компактная область из
- связная компактная область из
![]() - множество из
- множество из ![]() (множество визирования),
(множество визирования), ![]() на
на ![]() задана вектор-функция
задана вектор-функция ![]() (геофизическое поле),
(геофизическое поле), ![]()