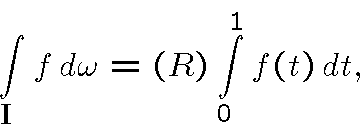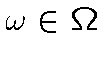
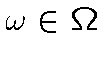
Пусть
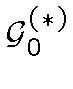 -- алгебра всех множеств
-- алгебра всех множеств ![]() ,
,
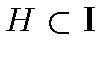 , измеримых по
Жордану относительно (счетно-аддитивной) меры
, измеримых по
Жордану относительно (счетно-аддитивной) меры ![]() , продолжающей
, продолжающей ![]() на алгебру
на алгебру ![]() подмножеств
подмножеств ![]() , порожденную
, порожденную ![]() .
Тогда для множеств из
.
Тогда для множеств из
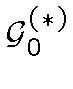 имеет место
совпадение, при
имеет место
совпадение, при
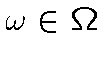 , значений меры Лебега и
, значений меры Лебега и ![]() .
Как следствие, для канторового дисконтинуума
.
Как следствие, для канторового дисконтинуума ![]() :
:
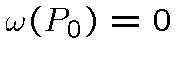 .
.
Если
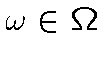 и
и
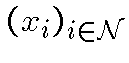 -- сходящаяся последовательность в
-- сходящаяся последовательность в ![]() , то
, то
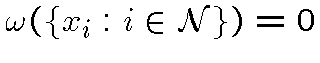 .
.
Вместе с тем, для непрерывных функций
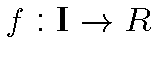 имеет место
имеет место
 :
: