ТЕОРЕМА 1.
Множество ![]() есть непустой выпуклый компакт
в
есть непустой выпуклый компакт
в ![]() -слабой топологии
пространства всех ограниченных к.-а. мер на
-слабой топологии
пространства всех ограниченных к.-а. мер на ![]() .
.
ТЕОРЕМА 2.
Множество ![]() содержит подмножество мощности континуума.
содержит подмножество мощности континуума.
ТЕОРЕМА 3.
Множество ![]() состоит только из неатомических к.-а. мер: если
состоит только из неатомических к.-а. мер: если
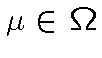 ,
,
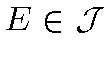 и
и 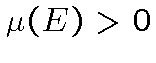 , то
, то
![\begin{displaymath}
\exists A \in {\cal J}:(A \subset E) \ \& \ (\mu(A) \in ]0,\mu(E)[).
\end{displaymath}](img33.gif)
Предложение.
Если
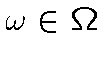 , то образ
, то образ ![]() при отображении
при отображении
![]() есть отрезок
есть отрезок ![]() :
:
![$\{\omega(H): H \in {\cal J}\}=[0,1].$](img34.gif)
Замечание.
Всякий элемент множества ![]() является чисто к.-а. мерой, не
обладающей свойством "ограниченной инвариантности". Именно, если
является чисто к.-а. мерой, не
обладающей свойством "ограниченной инвариантности". Именно, если
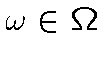 и
и ![$c \in ]0,1]$](img35.gif) , то можно указать множество
, то можно указать множество
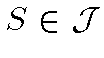 и число
и число
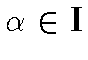 со свойством
со свойством
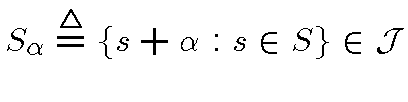 , для которых
, для которых
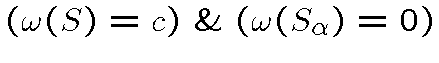 .
.